General Investigations of Rook Polynomials

Now that we’ve got a handle on Rook Polynomials, we can start asking what else we can do with them. Here are a couple of easy starting points.

Faster Decomposition

One thing we may want to do is think about how we can more quickly compute these polynomials. For small boards, the program developed in the previous post finishes execution fairly quickly. However, it is a recursive procedure, so for very large boards, there could be many decompositions needed. Furthermore, we could potentially run into stack overflow errors if we’re not careful.

Our decomposition was based on a single cell of the chessboard. Is it possible for us to decompose on something larger than a single cell? This is a question that was answered by Abigail Mitchell. She wrote a paper in 2004 which can be found here. Basically, Abigail’s idea was that if we could find certain kinds of “subboards” within a larger board, we could decompose on that subboard, instead of on a single cell.

First let’s talk about some terminology that will help us concisely describe what we’re doing.

Subboards

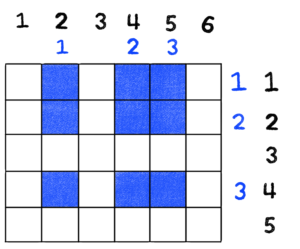
First, a “subboard” is basically just a board that is made up of a subset of the rows and columns of a given chessboard. For example, in the image above, we see a subboard (indicated by the blue squares) made up of rows 1, 2, and 4 of the given chessboard. It is also made up of columns 2, 4, and 5. In her paper, Abigail provides a more formal definition involving the use of injective mappings to describe which rows and columns are included. Using her definition, we have the following mappings.

The input to each mapping is the subboard’s row or column number, and the output is the given chessboard’s row or column number.

Covers

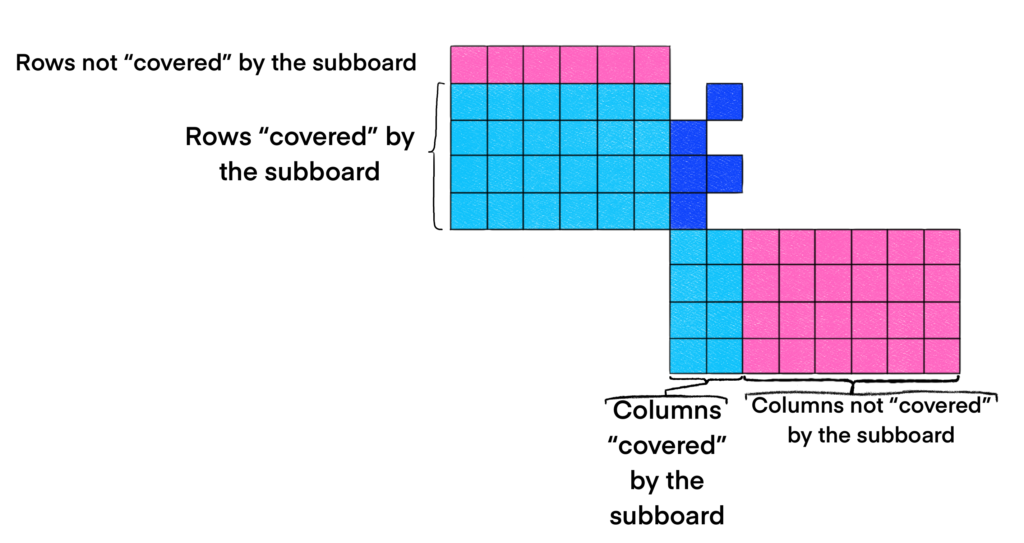
In the above example, the dark blue squares represent a subboard we want to examine. The cyan squares represent cells “covered” by the subboard, and the pink squares represent cells not “covered” by the subboard. In the paper and our discussion, we refer to covered rows and covered columns, but we don’t concern ourselves with individually covered cells.

This definition is important because it lets us know which rows of the subboard will be restricted when we place rooks in the chessboard (but outside of the subboard.) Any rook placements in a subboard will not affect the rook placements of any un-covered cells, and vice-versa. This idea is crucial to understand for our next definition.

Blocks

Consider the above example. Here, we’re going to consider a subboard’s covered rows and covered columns.

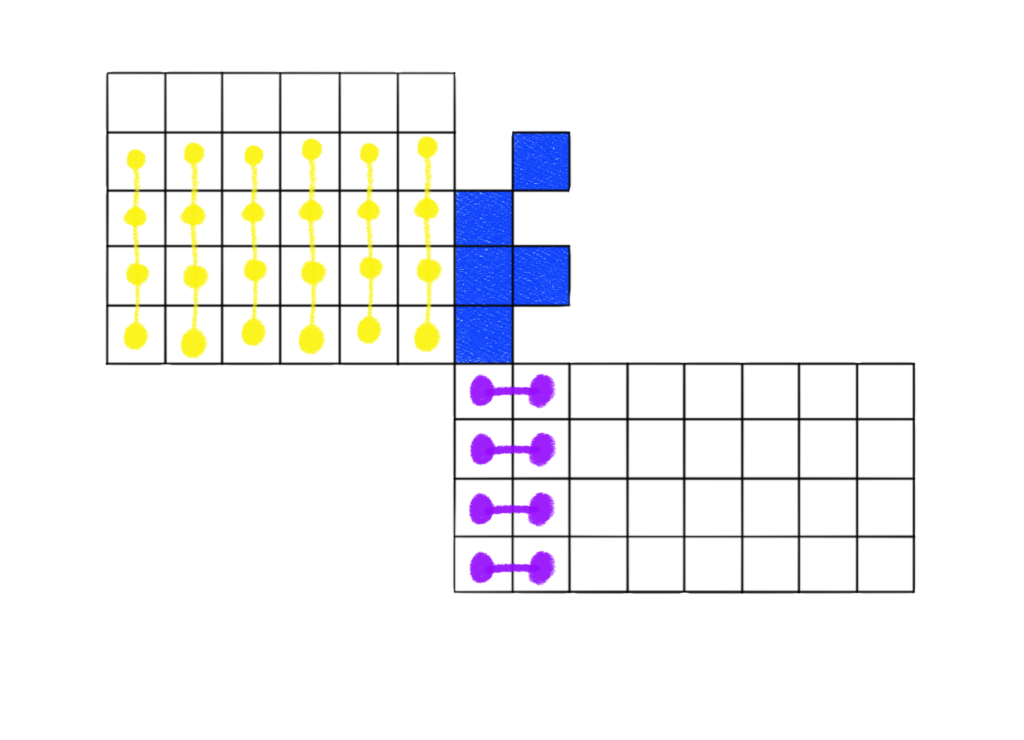
Notice that for the covered rows, I’ve linked together the uncovered columns with yellow markers. Similarly for the covered columns, I’ve linked together the uncovered rows with purple markers. To understand the definition of a block given in Abigail’s paper, we consider any linked columns and linked rows. Essentially, all the cells in a linked row or column must either all lack rooks, or they must all have rooks. In a valid rook placement, all linked cells will – of course – lack a rook. If this condition is met for all linked rows and all linked columns for a given subboard, then we call that subboard a block.

I thought this definition was a bit confusing at first because I initially did not understand the motivation for defining a block in this way. Thinking about the implications of the definition for 10 minutes, I was able to come up with this explanation. It helps to only examine one such linked row or linked column at a time.

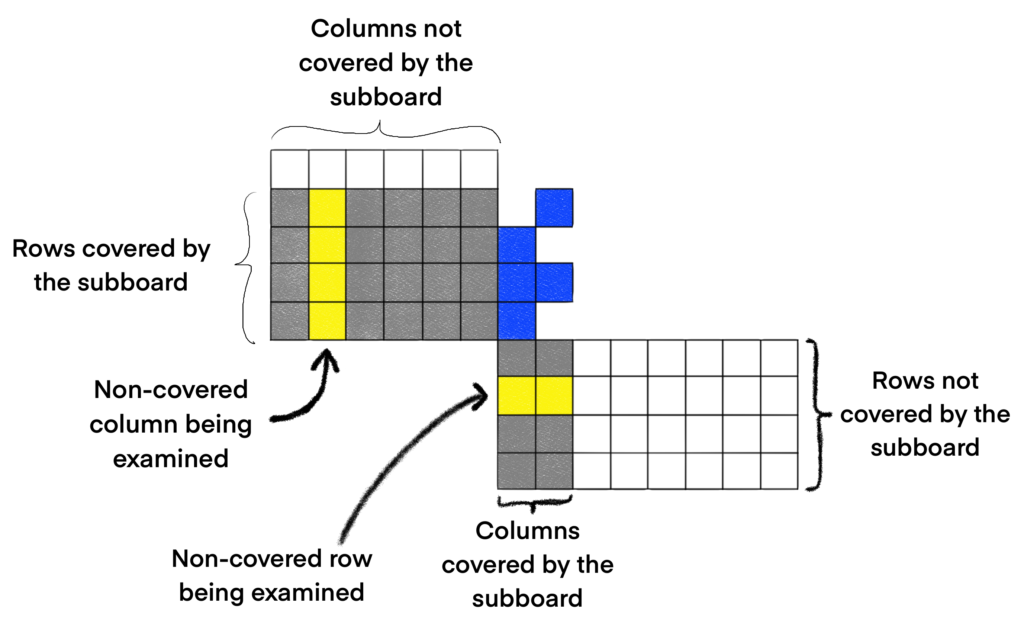
We’ll color any covered columns or rows we are not examining gray so we can more easily ignore them. We’ll color only one linked row and one linked column yellow to draw our attention to it.

Consider the yellow column in the diagram. Consider what happens if all cells in that column lack a rook, as depicted in this picture.

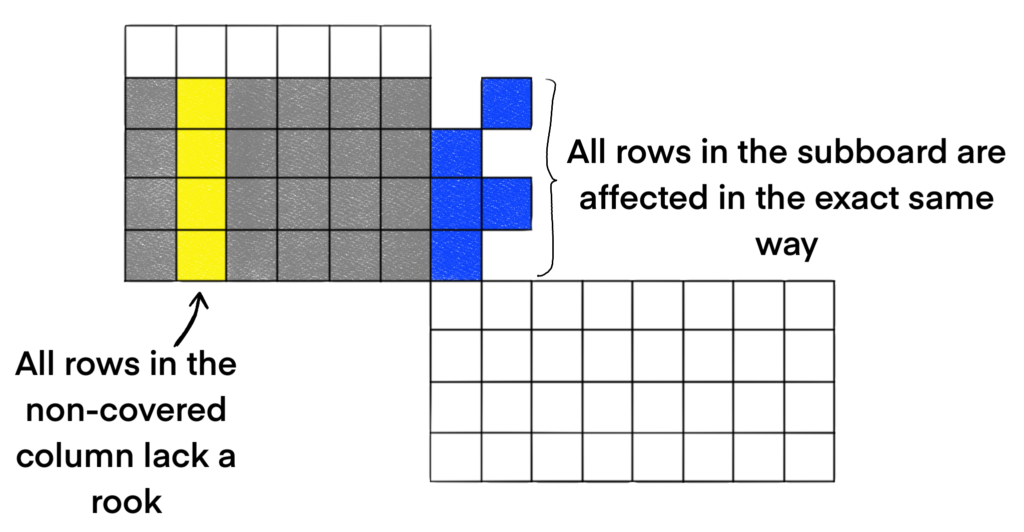
When all cells in that column lack a rook, notice that all cells in the subboard are still available. All rows of the subboard were affected in the exact same way in that all rows are still available for rook placements. Next let’s look at what happens when every cell in the non-covered column have a rook (this is an invalid placement, but still consistent with the requirement in the definition.)

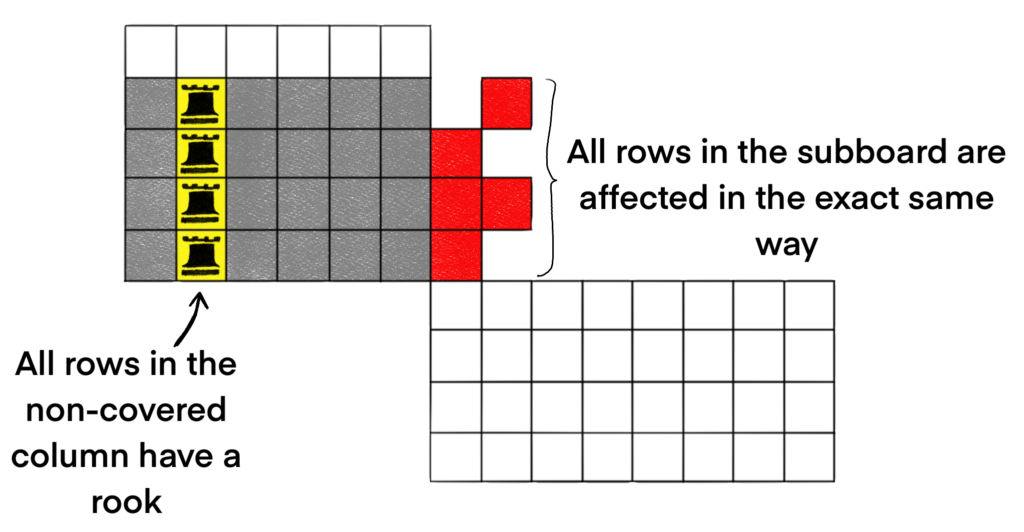
When all cells in the non-covered column have a rook, then all rows in the subboard are affected in the exact same way again. This time, all rows become restricted, so no rooks can be placed in the subboard.

In both cases, what happens for one row in the subboard happens for all rows in the subboard. For a subboard to be a block, we essentially need all rows to be affected in the same manner by what happens in a subboard’s covered rows and columns.

To make this idea more concrete, let’s look at what happens when only some of the cells in the uncovered column have a rook.

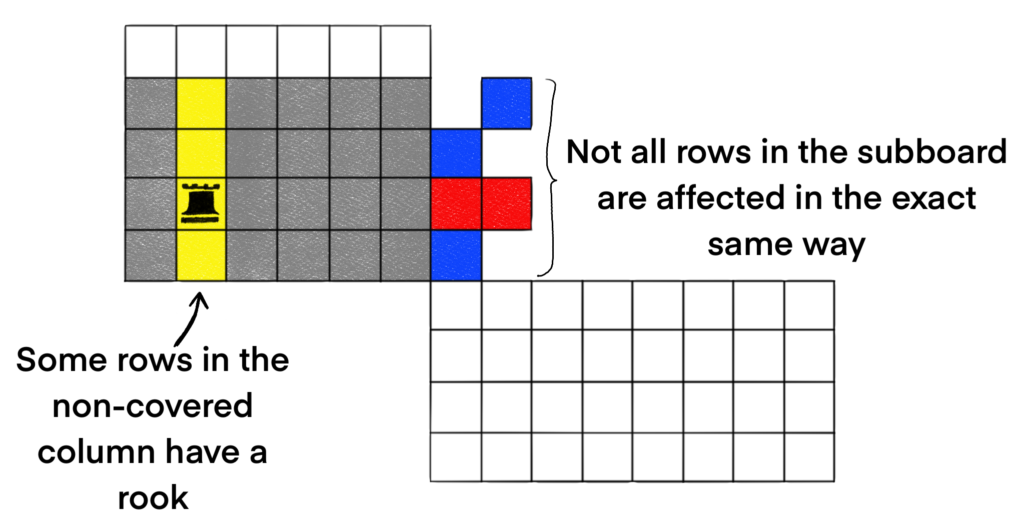
Notice that when only one of the cells in the uncovered column have a rook, then only some of the rows in the subboard are affected by the rook placement. The way we place rooks in the subboard now depends on the rook placements in the covered rows and columns.

The requirement that the cells in a linked column or linked row either all have rooks or all lack rooks allows the subboard to dictate what cells in any covered row or column can have rooks. This is why we define a “block” in this way: by having the block control where rooks can be placed in the outer board, we can use that block for decomposition.

This idea of blocks agrees with single cells of a chessboard. Now, we get to the heart of the paper: the Block Decomposition Theorem.

The Block Decomposition Theorem

Initially, when trying to calculate the Rook Polynomial of a board, all cells will lack a rook. This means that initially, any subboard will be a block. Using the same example we’ve been using, and keeping the same subboard as our block, we’ll decompose the board using the entire block, instead of only using a single cell. How do we do this? We use the Block Decomposition Theorem as described in Abigail’s paper. The formal statement and proof are given in her paper, so I’ll give a brief overview of the process.

First, we calculate the Rook Polynomial of the block we’re using for decomposition. This is easy enough to do by inspection, so I’ll just note that, using C_S to denote the chessboard determined by the block, we have that R(C_S, x) = 1 + 5x + 5x².

Next, we decompose by considering what happens when we place rooks in the block. In the single cell decomposition method, we either place a rook, or we don’t place a rook. In our block, we can place up to 2 rooks, so we have three cases to consider.

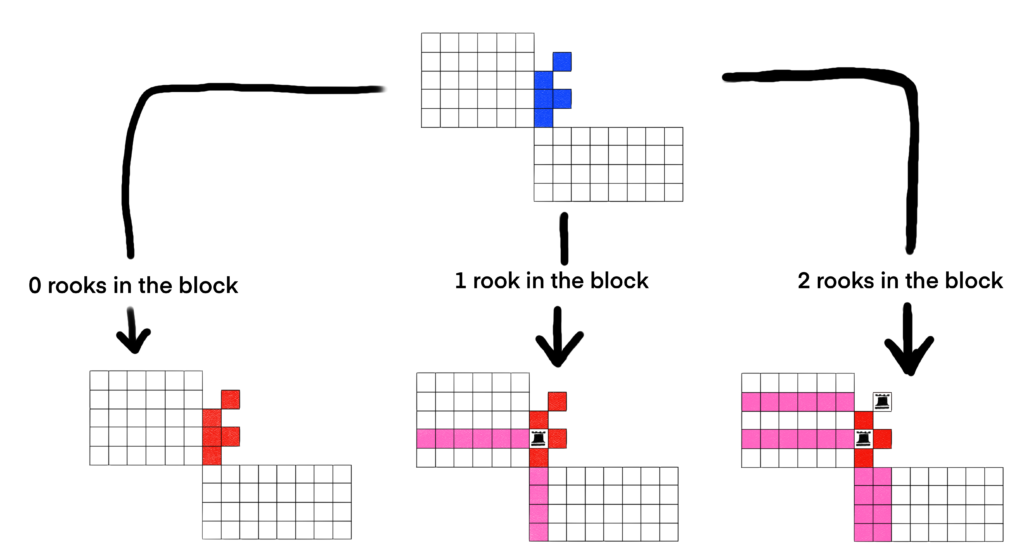
Note that when we place rooks in the subboard, we still restrict that row and column – both from the block and the outer chessboard – as usual.

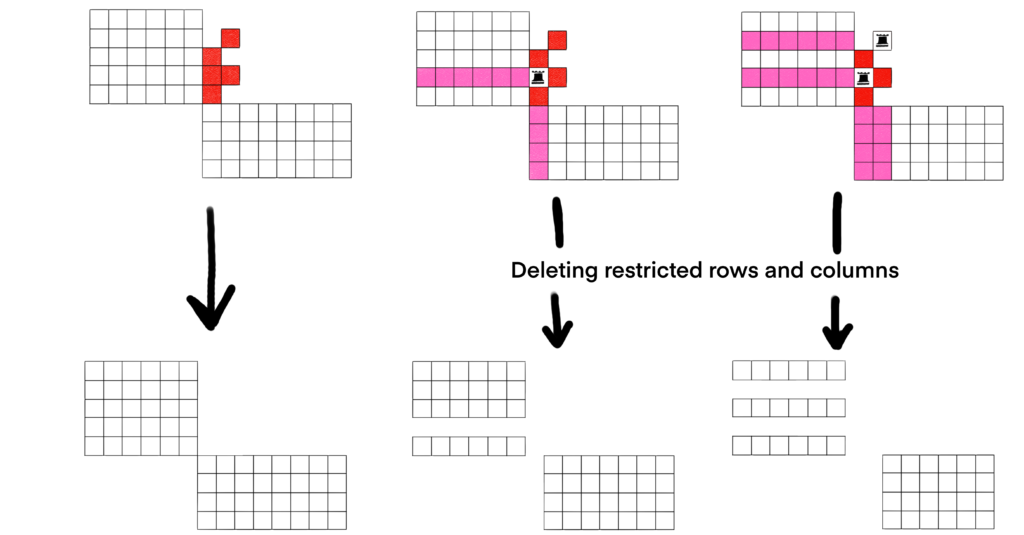
We can rearrange the rows and columns in each generated subboard to form full boards.

In all three cases, the subboards generated are made up up of two “disjoint” boards that are full. The Rook Polynomials for full boards, and for disjoint boards are relatively easy to workout, which means or choice for the block used for decomposition was a really good choice!

For our third step, let me just label each of these boards so they can be referenced.

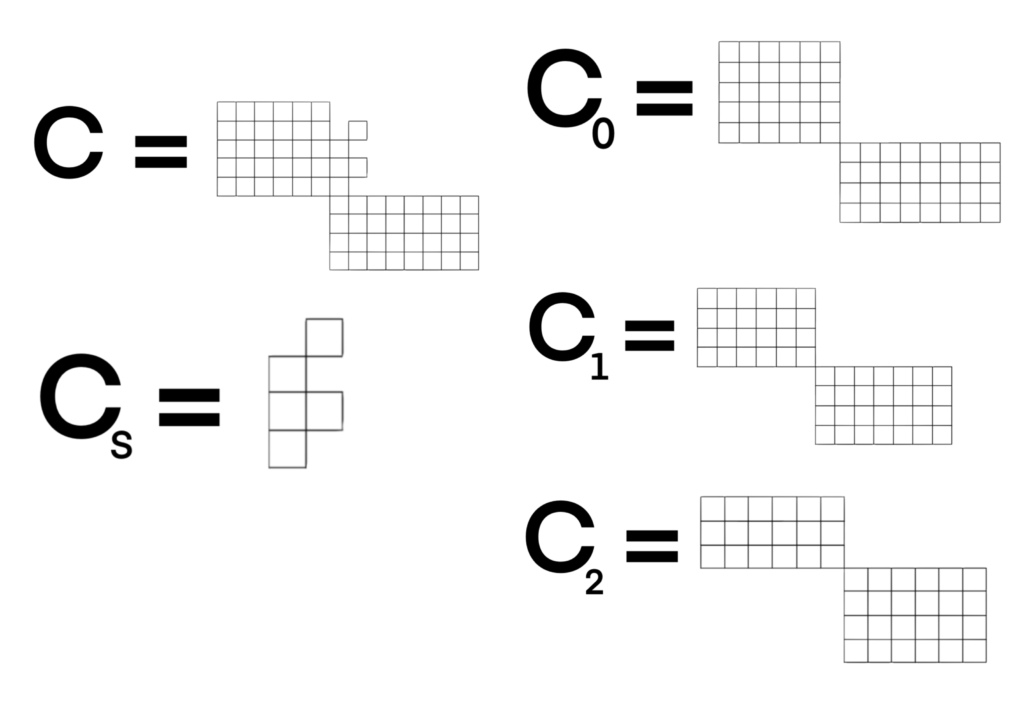
We are finally ready to perform the calculation. Remember that R(C_S, x) = 1 + 5x + 5x². We now have that, by the Block Decomposition Theorem, the following equation.

Notice that for the board we get from placing 0 rooks in the block, we multiply its Rook Polynomial by the part of the block’s Rook Polynomial corresponding to 0 rooks (1). Similarly, for the board we get after placing only one rook in the block, we multiply that board’s Rook Polynomial by the term in the block’s Rook Polynomial corresponding to 1 rook (5x). The same thing happens with the board obtained after placing two rooks in the block.

Notice that when we use a single cell as a block, this is exactly how we previously calculated the Rook Polynomial because the Rook Polynomial for a single-cell block is simply 1 + x.

Possible Next Steps

We saw an example of how we can choose a block on a board that is “nearly” disjoint. What if the board we’re dealing with is not “nearly” disjoint? Are there any ways to determine which blocks are the “best” blocks? By that, how do we choose blocks that minimize the number of decompositions we need to use? Remember when doing single-cell decomposition, we may have to decompose several times, which is where the bulk of the algorithm’s work is spent. The same is true for block decomposition.

We could use large blocks, but then a lot of time will be spent computing that block’s polynomial. Is it possible that we spend so much time computing the Rook Polynomial of the large block that we lose any gains by having small subboards after decomposition? On the other hand, if our block is small, then the generated subboards will be large, requiring more decompositions. What’s the sweet spot in terms of block size?

Suppose we had someway of figuring out that some efficient block size exists for our board. How do we determine what that block is? In our current method, we can only determine how good our block choice is after performing some decompositions. How do we automate the process of selecting good blocks?

At the end of her paper, Abigail mentions this as the next step. I thought this was such an intriguing paper, and reading through it again has inspired me to take up this question.

3D Boards

One of the first things I thought about when starting my thesis work was about 3D boards. When searching for research material, I stumbled upon this paper by Nicholas Krzywonos and Feryal Alayont.

Some of the applications I talked about in my first post can easily be extended in 3 dimensions, but now care must be taken. How do rooks capture other rooks in 3 dimensions? Do they capture along hyperplanes, or in lines? What implications does either capture rule yield?

By hyperplanes, I of course mean what is depicted in the following picture.

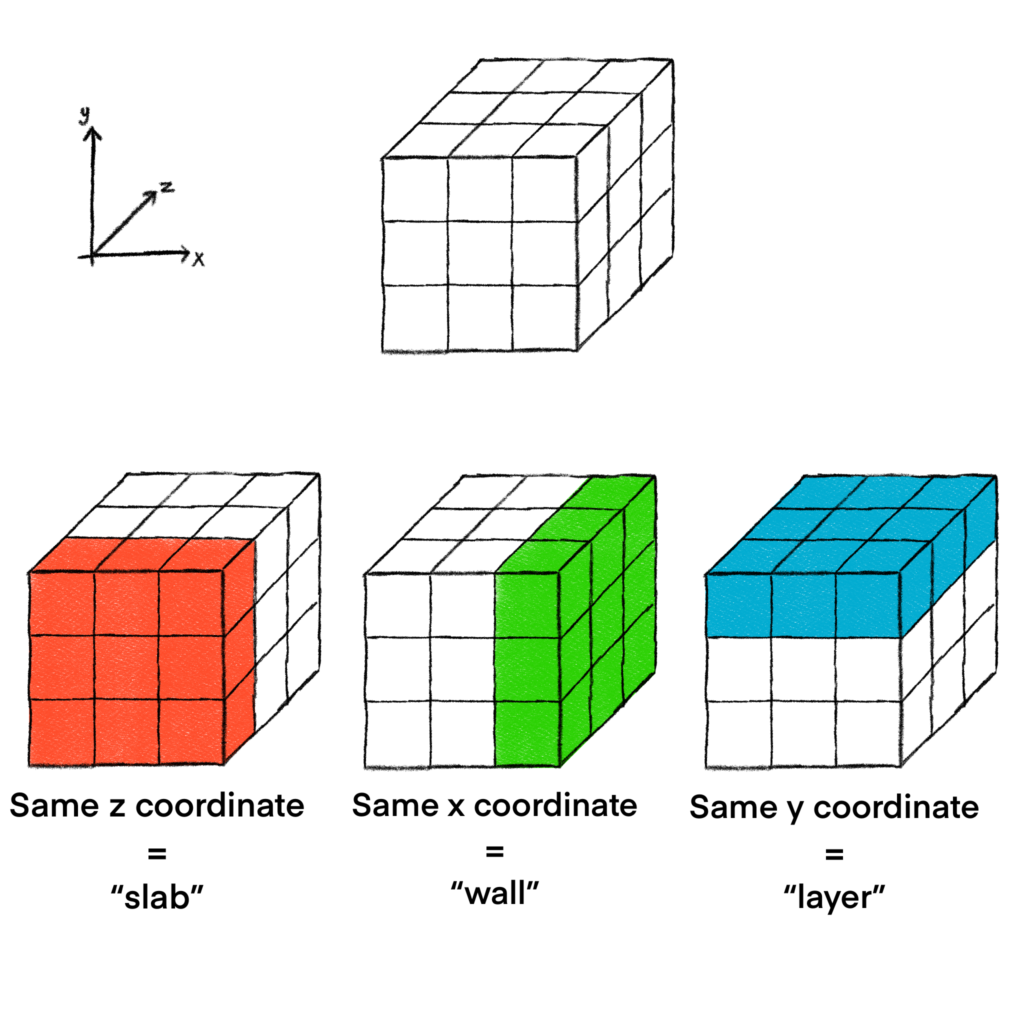
When doing assignment problems, this will yield different results that when rooks capture along lines, as depicted in this image.

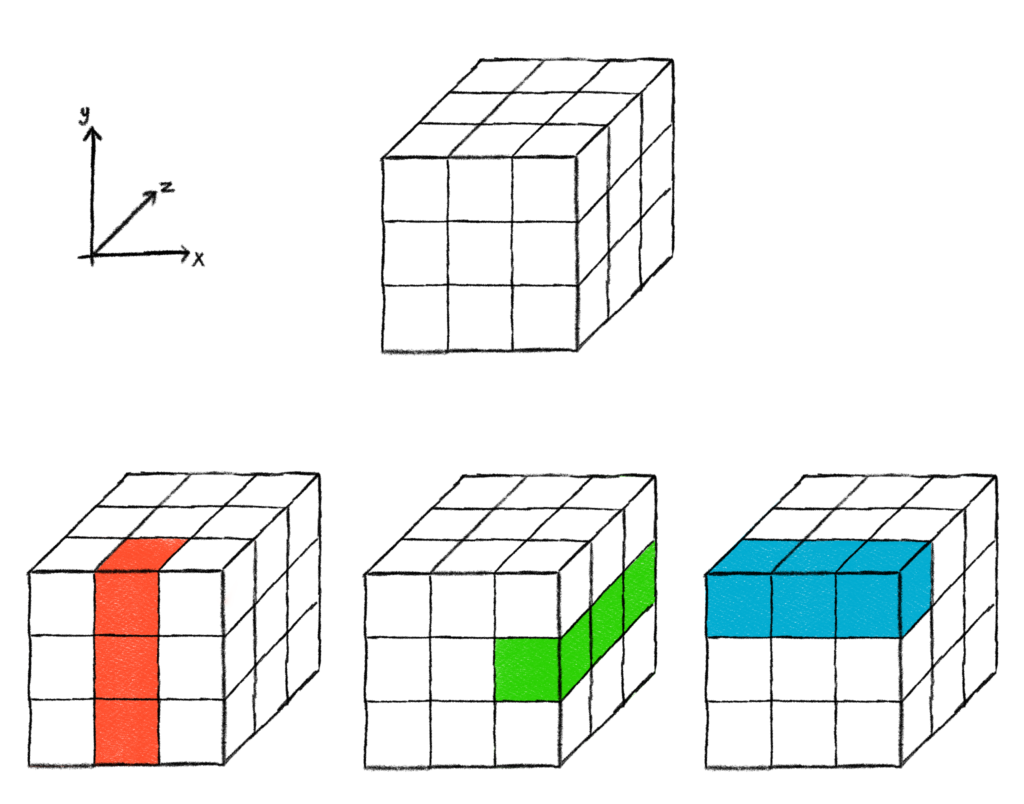
I went in a different direction for my research, but Krzywonos and Alayont found interesting connections between special types of 3D boards and special number sequences which I’ll briefly describe here. Note that the following results were obtained by considering rooks that attack in hyperplanes, and not lines.

Triangular Boards

What happens when we stack cells in a triangular fashion, as depicted below.

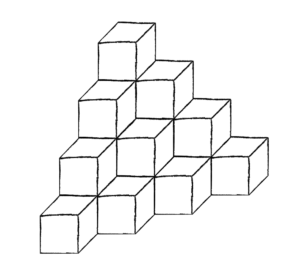
The authors found a connection between the Rook Polynomials of triangular boards and central factorial numbers.

Genocchi Boards

What happens when you start off with an n-by-n-by-n board, and take off one of the (n-1) triangular boards? You get the following board.

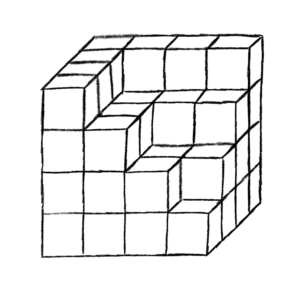
The Rook Polynomials of these boards are related to the Genocchi numbers, hence this kind of board is called a Genocchi Board.

Derangement Boards

Rook Polynomials provide a way to calculate the number of derangements, simply by restricting the diagonal cells of a square (that is, a 2D) board from any rooks. For a 3D board, we can extend the idea by restricting all cells along one of the diagonals. For a 3-by-3-by-3 board, here is one such diagonal.

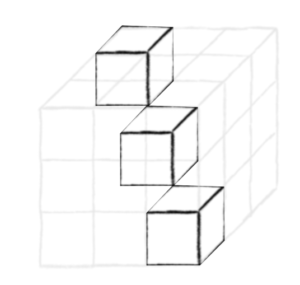
By restricting these cells from any rooks at the outset, the associated Rook Polynomials are related to the 3-by-m Latin squares. As pointed out by the authors, for any dimensional board d, the derangement board of size m is related to the number of d-by-m Latin rectangles.

Possible Next Steps

As should be evident by now, specially designed boards lead to special Rook Polynomials. What kind of other boards can we design? What kinds of properties will those specially designed boards have?

Going in the other direction, given a special sequence of numbers, can we design boards that yield related Rook Polynomials? For example, are there “Fibonacci” boards? Are there “Catalan” boards? Are there any boards that yield the Stirling numbers of the first or second kind?

Remember that the authors only considered rooks that attack in hyperplanes, and not lines. We can ask the same questions above for 3D rooks that attack in lines instead of hyperplanes.

Other Chess Pieces

There are other chess pieces we could consider.

Bishops

Bishops are perhaps the most natural non-rook piece to consider, seeing as they are basically the same thing as a rooks, just going diagonally instead of vertically or horizontally. I’ll have more to say about this shortly.

Knights

Knights arguably have the second weirdest movement pattern. Being able to count how many ways you place any number of knights on a board has interesting implications. Using similar decomposition techniques discussed earlier should work here as well. Do these polynomials yield any interesting integer sequences? Do these polynomials lend themselves well to any application as the Rook Polynomials do?

Pawns and “Directed” Boards

Pawn movement is arguably weirder than knight movement because pawns capture in a fashion that is different than non-capture movement, whereas knights capture in the exact same way they move. In other words, pawn movement is conditional upon whether or not a pawn can capture or not.

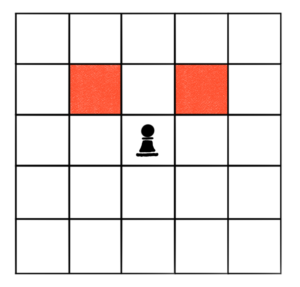
When calculating polynomials of a board, we don’t allow pieces to move, we only allow them to capture. What does this mean for pawns? Well, pawn capture is not only dependent on position, but color as well. Pawns can only capture in one direction. White pawns capture in a direction away from the white king, and the same is true for black pawns and black kings. This method of capture can possibly give rise to the notion of an “oriented” or “directional” board, where pieces can only capture in one direction.

This was an idea proposed by my thesis advisor. I didn’t spend too much time thinking about this problem, but like everything else related Rook Polynomials, it is such an interesting idea to think about what kinds of implications imposing an orientation can have on polynomials.

Queens and Kings

Thinking of the last two pieces, we could note that kings move in similar way to queens, but of course queens can move more than one square at a time.

Possible Next steps

What kinds of boards can we design using an orientation? What problems can we solve with Bishop Polynomials, Knight Polynomials, or Pawn Polynomials? What about queens or kings? If we were to calculate the King Polynomial and Queen Polynomial of a board, could we somehow relate the two? It feels like we should seeing as how kings can move in all directions just like queens.

What happens if we have multiple types of pieces on a board? What would such a polynomial look like?

What Questions Did I Attempt to Answer in my Thesis?

For my thesis, I focused on bishops. As noted earlier, they behave in a somewhat similar fashion to rooks, so extending the results wasn’t too much of a hurdle. Next time, we’ll talk more about bishops, and we’ll see how Rook Polynomials and Bishop Polynomials are related.