Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124


In a previous post, I described a set of Python functions within a script that can calculate Rook Polynomials for a board. A lot of that material can be reused, and some of it will serve as a guide to help us develop more algorithms for calculating Chess Polynomials using rooks and bishops. Some care will need to be taken to make sure the algorithm works perfectly, so let’s talk about some difficulties we’ll need to address.
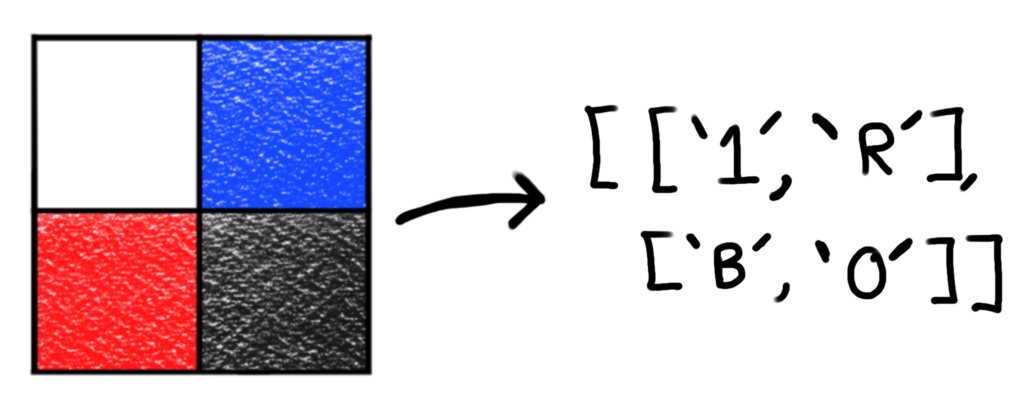
So far, we’ve described boards using a list of lists. Each inner list would represent one row of the board. In each of those inner lists, a ‘1’ would represent an open cell, and a ‘0’ would represent a restricted cell. This works extremely for a single type of piece.
As we’ve seen in the previous post of this series, we’ve seen that if we have two types of pieces, we may need to restrict cells from only one of the pieces, while allowing the other piece to be placed if needed. A such, we came up with a color-coding scheme to represent which cells were restricted only to rooks, and which cells were restricted only to bishops. We can do the same thing in our lists of lists representation of boards.
Instead of using colors, we’ll use a ‘R’ character to represent a cell that is open only to rooks. Likewise, we’ll use a ‘B’ character to represent a cell open only to bishops. We’ll still use a ‘1’ character to represent a cell that is open to all pieces, and a ‘0’ character to represent a cell that is restricted from all types of pieces.
We need to keep track of two variables. In order to be able to choose which term we want to examine, we need to specify the exponent of both variables, hence we’ll need a two-dimensional object to represent a multinomial. A matrix fits this purpose, and in Python, a matrix is maintained as a list of lists. We calculated the Chess polynomial of the 2-by-3 board in the previous post. Here is the multinomial represented in matric form.
| Power | r0 | r1 | r2 |
| b0 | 1 | 6 | 6 |
| b1 | 6 | 4 | 0 |
| b2 | 11 | 0 | 0 |
| b3 | 6 | 0 | 0 |
| b4 | 1 | 0 | 0 |
In code we would represent this list as such:
[[1, 6, 6].
[6, 4, 0].
[11, 0, 0],
[6, 0, 0],
[1, 0, 0]]
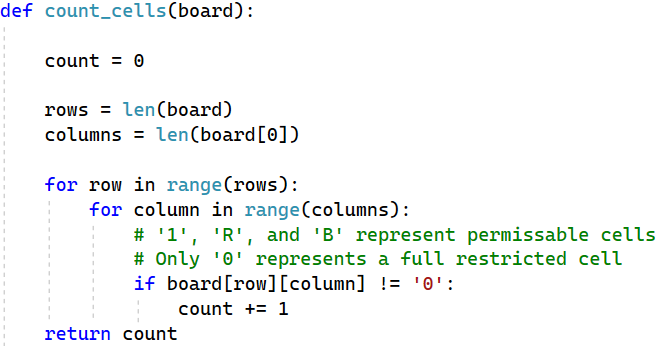
Just as we’ve done previously, the first thing we need to do is count the number of cells on which we can decompose. We can decompose on any cell that is not fully restricted, so we’ll count all cells that do not store a ‘0’. This will be useful when deciding if we are in some sort of base case.
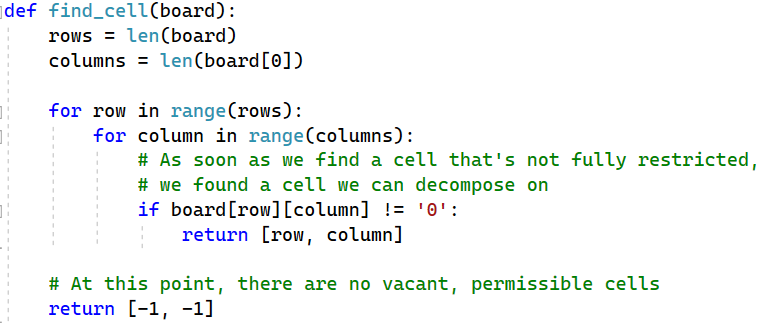
The next thing we want to do is find a cell on which we could decompose the board. If there are cells that are not fully restricted, we can decompose them, even if they are open only to one type of piece.
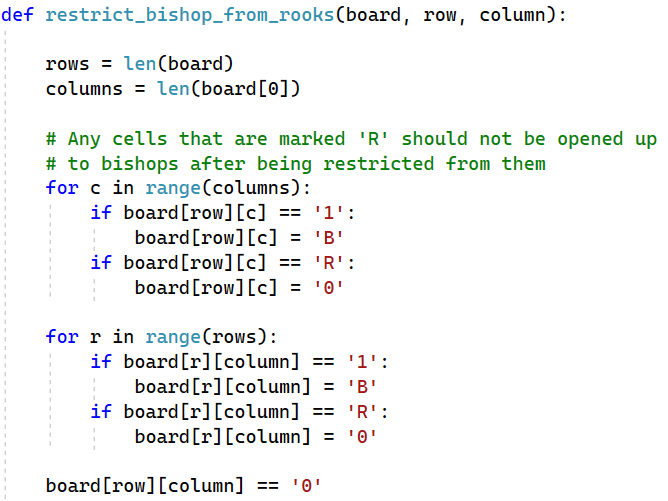
When we decompose a board using a specific type of piece, we’ll want to make sure that the newly placed piece will not be captured by a future piece. In this case, when we place a bishop on a cell, no other cell in that row or column can have a rook as this would lead to a capture.
We should be careful here though. If one of the cells in that same row or column has already been restricted from a bishop, then by restricting it from rooks as well, that cell becomes totally restricted. This means we need to examine what restrictions are currently placed on a cell before imposing a different type of restriction.
If a cell is totally open, then we can safely restrict it from rooks without affecting other placements. If the cell is already restricted to rooks, we need to make sure it gets a ‘0’, indicating that it is restricted from all other pieces. It is not enough to just set every cell in the same row or column to ‘R’, because that could open up restricted cells when they were previously restricted from rooks.
This is what I’m doing in this function.
Just as we have to be careful when restricting a cell from a rook, we have to be careful when restricting cells sharing a diagonal from bishops. We must make sure no rook gets subsequently captured by a bishop.

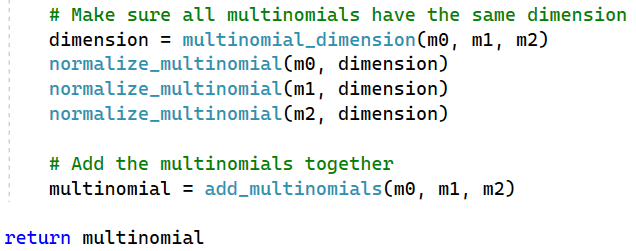
Just as adding lists with the same number of elements is easier than adding lists with different lengths, it is easier to add matrices together if they have the same dimension. In order to be able to “re-dimension” our matrices to have this happen, we’ll need to know what the dimension of all matrices should be. Remember we’re using matrices to represent our multinomials. This process will help us calculate the final multinomial.
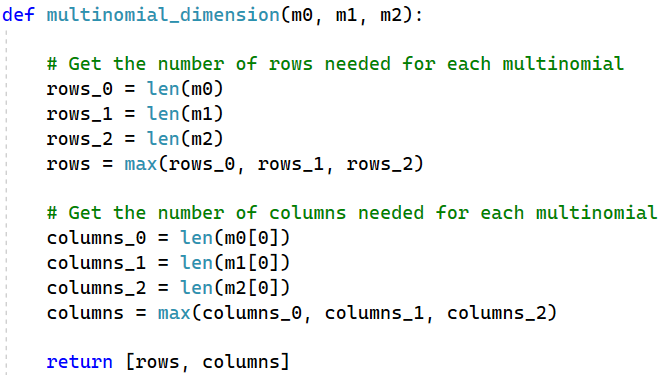
In this procedure, we make sure that each matrix (or multinomial) actually has the same dimension. This will make adding them together for the final result easier.
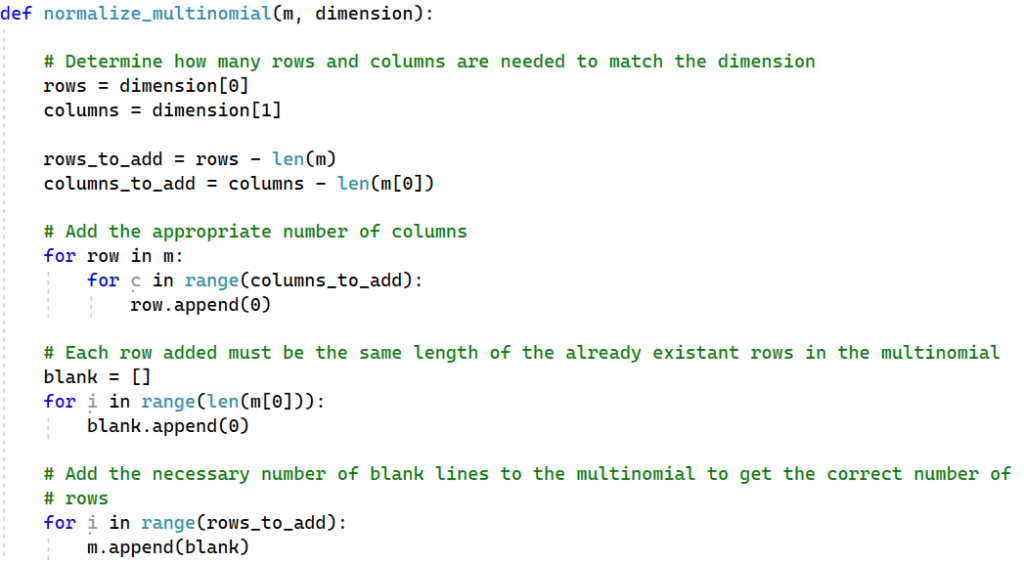
Once we’ve decomposed our board, and we’ve obtained the associated multinomials, it’s time to add them together for the final result. That is exactly what this procedure does. This is done via normal notions of matrix addition.

With all of these utilities now defined, we are in a position to start calculating the Chess Polynomial we want. Because of the recursive nature of decomposition, we’ll once again use recursion to handle the computation.
If we decompose a board, and are left without any cells, we know there is only one way to place any number of rooks and bishops, which is just to not place any such pieces on the board. So we can return the trivial Chess Polynomial.

It’s pretty easy to determine what the Chess Polynomial of a single cell is. Thus, if we decompose and end up with a single cell, we’ll be able to return what that cell’s Chess Polynomial is.
If the cell is open to all pieces, then the associated Chess Polynomial is 1 + r + b. This is represented by the matrix [[1, 1], [1, 0]]. For cells open only to rooks, the Chess Polynomial is 1 + r. This is represented by the matrix [[1, 1]]. For cells open only to bishops, the Chess Polynomial is 1 + b. This polynomial is represented in Python code as [[1, 0], [1, 0]].
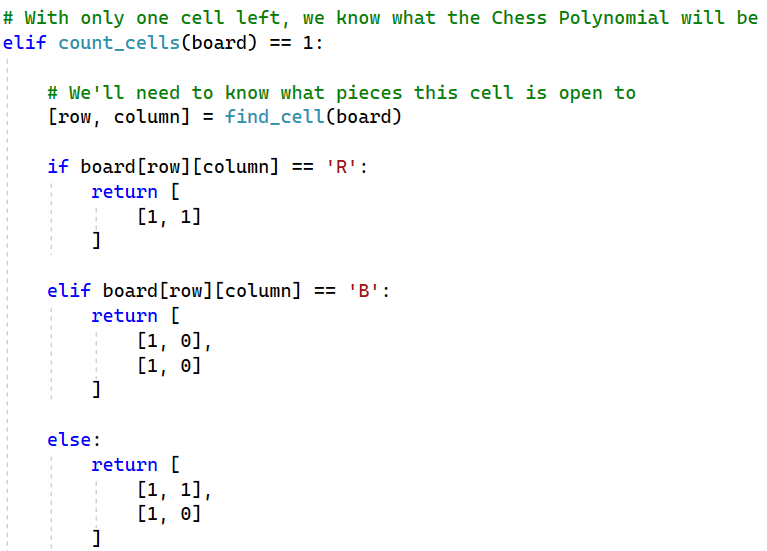
At this point, we are not in a base case, so we’ll need to decompose.
The first thing we do is find a cell on which to decompose. This cell can be restricted from all pieces upon decomposition, so we’ll go ahead and get its multinomial.

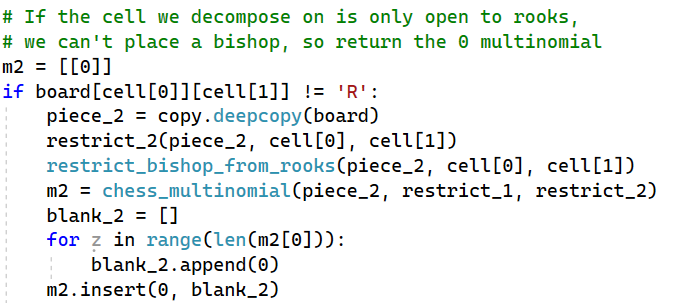
If the cell is only open to bishops, we need to make sure that the associated multinomial is just the 0 multinomial. This will prevent us from adding any rooks that lead to captures. We can check what the cell is open to, and if it is open to rooks, then we can decompose and get the multinomial.
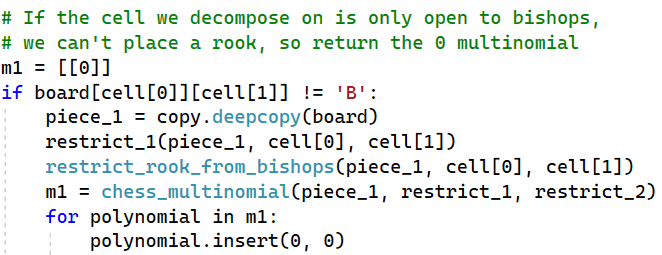
Just as we did for rooks, we don’t want to contribute any bishops to the multinomial if this cell is not open to bishops. If this cell is restricted from bishops, then we can just use the 0 multinomial. Otherwise, we’ll decompose and find the multinomial associated with a bishop placement.
Here, we just make sure all multinomials have the same dimension. As was done with regular polynomials, we can do this by appending 0s to the end of every list. Once we’ve done that, we just return the sum of all multinomials.
We’ll want to be able to see what our final result is in a meaningful way. The basic idea is that we’ll print out any non-zero terms using their variables and exponents.

The output will look similar to the way described in this post of the series. Let’s take a look at a couple of examples.
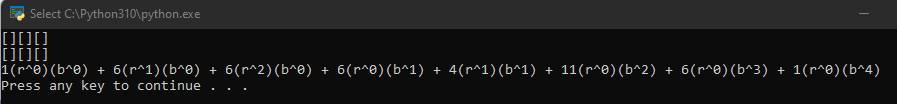
These results agree with what we found in the previous post. This was a sight for sore eyes after receiving so many stack overflow errors.
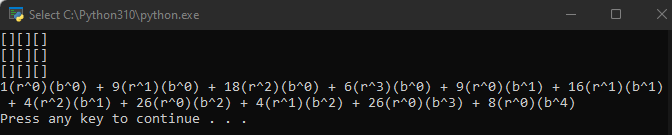
If we pick out the terms without any b component, then we have the Rook Polynomial for the full 3-by-3 board we’ve calculated so many times in this series of posts.
Great!
I’ve updated the GitHub repository with this new script, and it is ready for use.
As far as what we’ll be talking about next, we’re going to examine one more type of chess piece that shares a lot of features with both rooks and bishops.
Stay tuned.