Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Unions and Intersections of Sets
The types of open sets and closed sets examined thus far are perhaps the simplest types available. Since these are examples of sets, that means they can be used as building blocks for building larger, more complicated types of open sets and closed sets respectively. The main tools used to combine sets are the union and intersection operations. But can we guarantee that when performing a union or intersection on open sets we end up with an open set? Can we guarantee that unions and intersections of closed sets lead to more closed sets? Here, we’ll examine several different scenarios.
Combinations of Open Sets
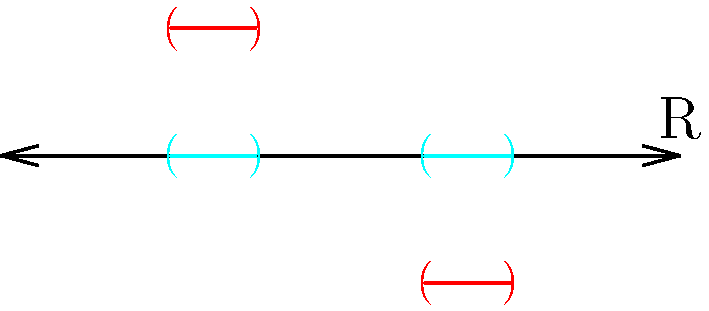
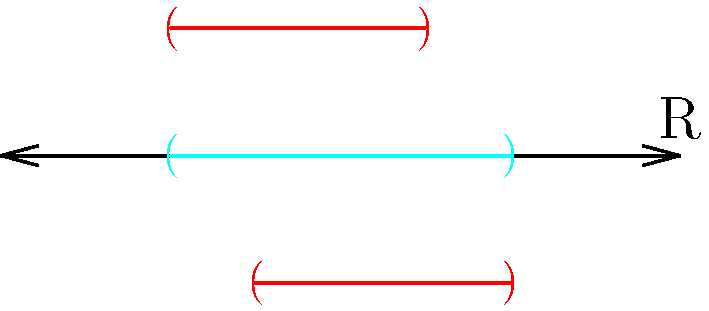
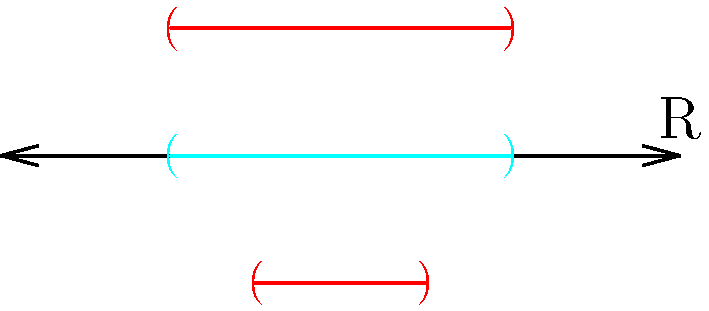
Figure 1: In general, for any two open sets, there are three situations to consider when taking their union. The individual intervals are colored red, while the union is colored cyan. In (a), we have no overlap. In (b), we have some overlap. Finally, in (c) we have total overlap. In all cases, the size of each interval, is no smaller than the smallest interval used in the union. Since all points in all sets are also present in the union, we may suspect that any interior points in the individual sets are also interior points of the union.
Theorem 1
Suppose {Uɑ} is a (possibly infinite) collection of open sets where ɑ is an element of some index set I. Then,
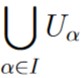
is an open set.
General Strategy: We can appeal to the definition of open set to show this. We pick an arbitrary point in the union, and show that it is an interior point. The point will be in one of Uɑ, and since it is a point of an open set, it will be an interior point of Uɑ.
Suppose p is a point such that
As such, because we’re taking a union of sets Uɑ, this means that there is some β ∈ I such that
p ∈ Uβ.
Notice that since Uɑ is an open set for all ɑ ∈ I, and because β ∈ I, we have that Uβ is an open set.
Now notice that because p ∈ Uβ and that Uβ is an open set, there exists some r > 0 such that
Nr(p) ⊆ Uβ.
But remember that
Thus, we must also have that
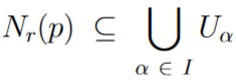
thus making p an interior point of .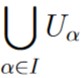
Since p was an arbitrarily picked point of 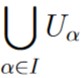, and because p is an interior point of 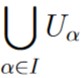, we must have that every point in 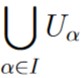is an interior point of .
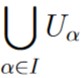Thus, 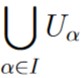must be an open set by definition.
With this theorem, we are now able to formally prove that any interval of the form [a, b] is a closed set.
Corollary to Theorem 1
Any interval of the form [a, b] with a, b ∈ ℝ is a closed set.
Because (-∞, a) is an open set, and (b, ∞) is an open set, we have that
(-∞, a) ∪ (b, ∞)
is also an open set. Then by taking the complement of this set, we get
(-∞, a)C ∩ (b, ∞)C = [a, ∞) ∩ (-∞, b] = [a, b].
Thus, according to the topological definition of a closed set, since [a, b] is the complement of an open set, it must be closed as desired.
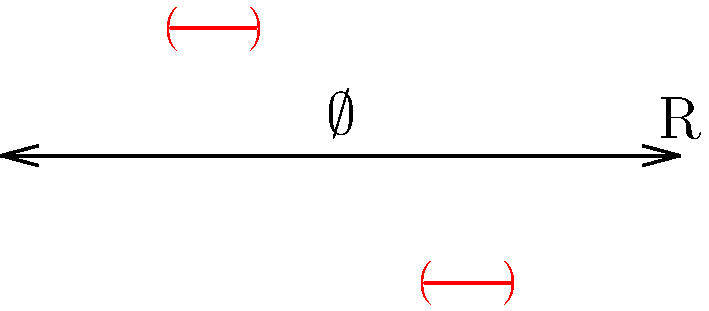
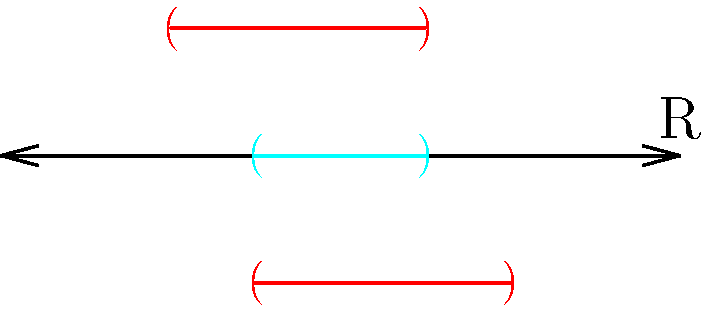
Figure 2: When we take the intersection, we tend to end up with new sets that are no larger than the smallest component interval. In (a), with no overlap, we end up with ∅. In (b), we have some overlap, and in (c), we have total overlap. Again, the individual intervals are colored red, while the intersection is in cyan.
Now we turn to intersections of open sets. As demonstrated in Figure 2, intersections tend to be smaller than their component intervals.
Theorem 2
Suppose 
is a finite collection of open sets. Then,
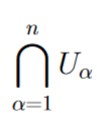
is an open set.
General Strategy: We will presume that the intersection of all of these open sets is actually not open. Then one of the points in the intersection will not be an interior point. But, since this point is in every set (all of which are open), it’s an interior point of all those sets. This will yield a contradiction.
Presume – for the purpose of showing a contradiction – that
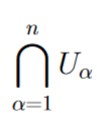
is actually not open. Then there is some point p ∈ 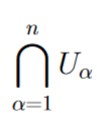that is not an interior point of .
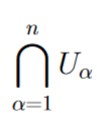Note that since p ∈ 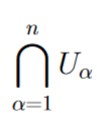, we must have that p ∈ Uɑ for all ɑ ∈ {1, 2, 3, .., n}. Because each Uɑ is open, this means that p is an interior point for every Uɑ.
By definition of interior point then, there exists r1 > 0, r2 > 0, r3 > 0, …, rn > 0 such that
N1(p) ⊆ U1, N2(p) ⊆ U2, N3(p) ⊆ U3, …, Nn(p) ⊆ Un.
Let r = min(r1, r2, r3, …, rn), then we have that
Nr(p) ⊆ U1, Nr(p) ⊆ U2, Nr(p) ⊆ U3, …, Nr(p) ⊆ Un.
Now, because Nr(p) ⊆ Uɑ for all ɑ ∈ {1, 2, 3, .., n}, we have that
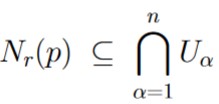
So, we just found a neighborhood, centered at p, that is a subset of 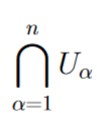, making p an interior point of 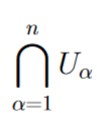. However, this contradicts the fact that we chose p to not be an interior point of .
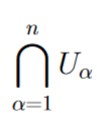Therefore, 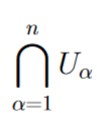must be open as desired.
Infinite Intersections of Open Sets
Notice that in the theorem about intersections of open sets, we had a finite collection of open sets. Hence, the theorem guarantees that the intersection of a finite number of open sets will be open. This theorem says nothing about an infinite intersection of open sets. Can we say anything about infinite intersections of open sets?
Example 1
Let’s come up with an example of an infinite intersection of open sets that is also open.
Start with the empty set ∅, which is known to be open. We might notice that since
(-1, 0) ∩ (0, 1) = ∅
we could extend this by considering all open intervals of the form (n, n + 1). When n and m are distinct integers, we would also have that
(n, n + 1) ∩ (m, m + 1) = ∅.
This means that
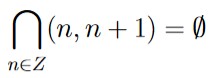
is an infinite intersection of open sets that also yields an open set.
Example 2
Can we come up with an infinite intersection of open sets that is not open?
We would need to produce a set E with a point p where no neighborhood centered at p is a subset of E. We know that finite point sets are not open, so can we produce a finite point set using an infinite intersection of open sets?
If we nest a bunch of open intervals inside of each other, and take the intersection of all of those open intervals, then we end up with a much smaller open interval. If we only take a finite number of open intervals, we always end up with an open interval with infinitely many points. So, let’s try taking an infinite number of nested open intervals.
Consider
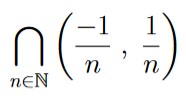
Is 0 in this set? Consider that for all n ∈ ℕ we have that
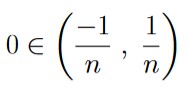
Thus we have that
.
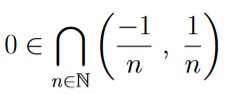Now consider the fact that for any real number k such that k > 0, there exists some natural number n such that
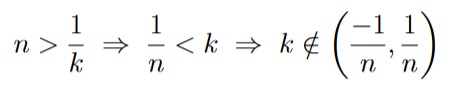
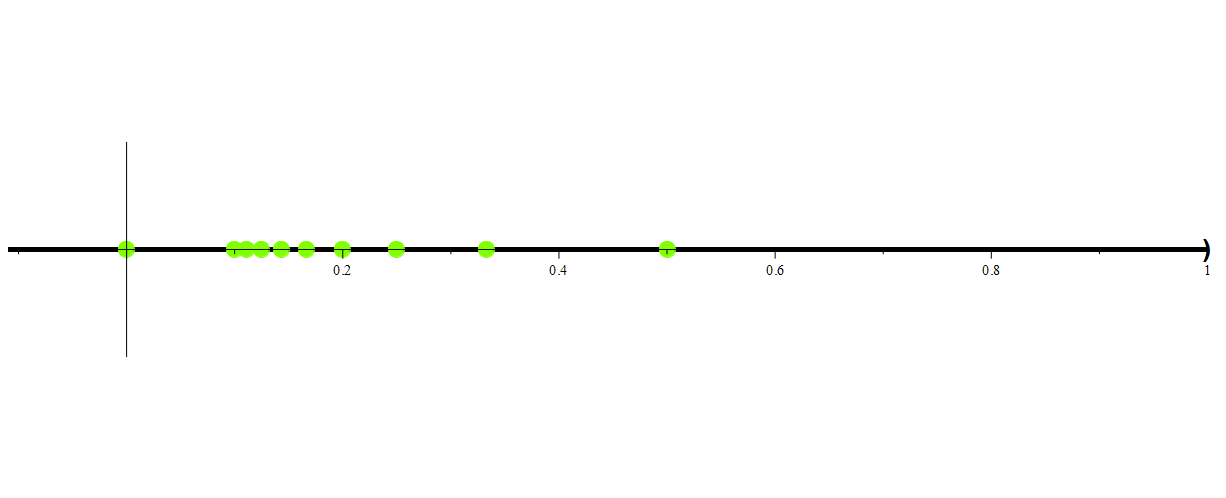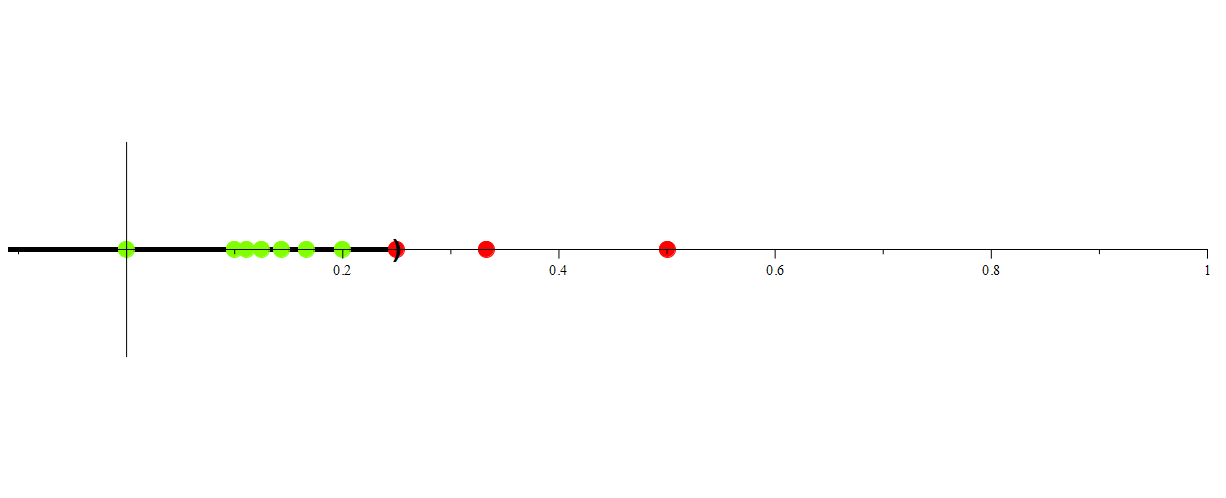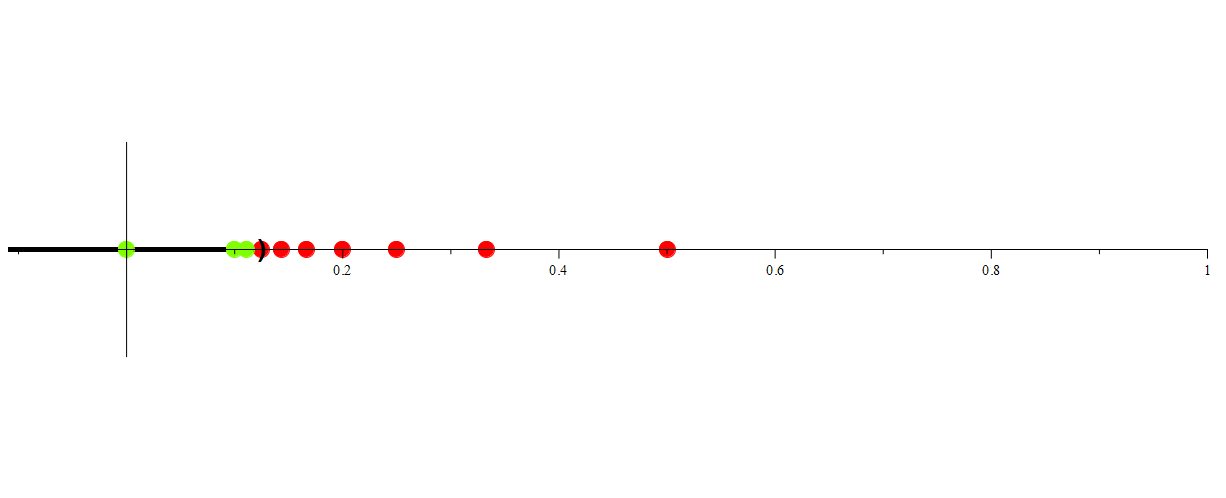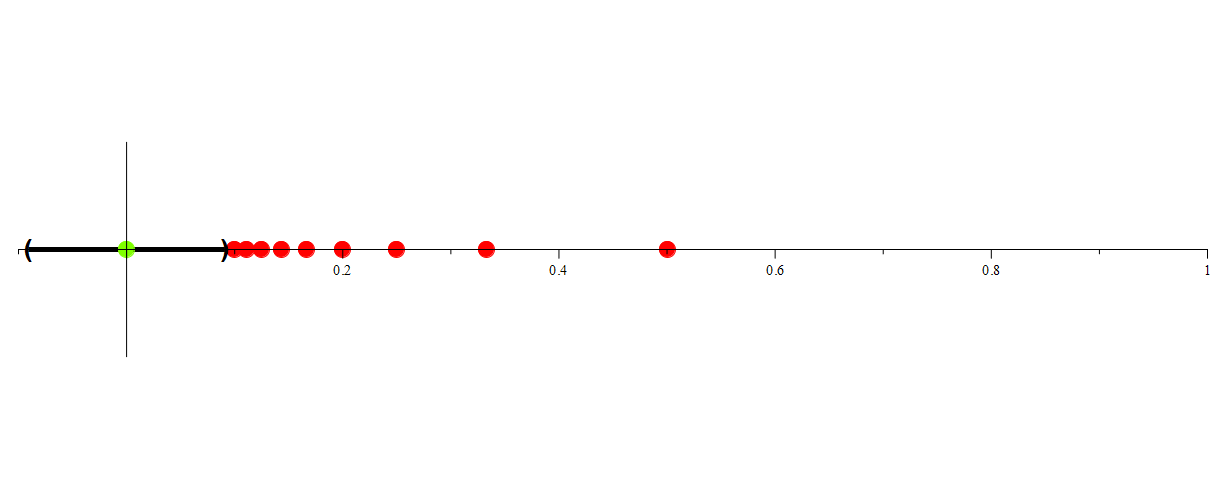
Thus, if we take the intersection of every interval of the form 
, k will be eventually be excluded from one of those intervals (including all subsequent intervals), and hence will not be in the intersection. Thus, we have that
.
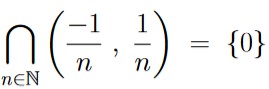Since finite point sets are not open, 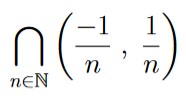is an example of an infinite intersection of open intervals that is not open.
Combinations of Closed Sets
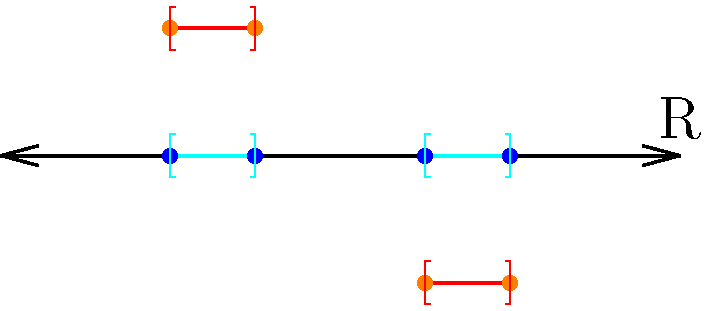
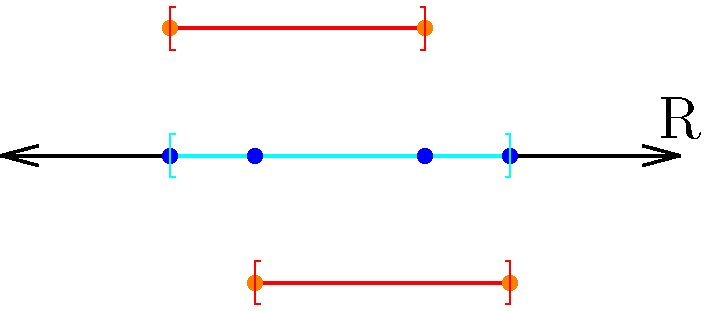
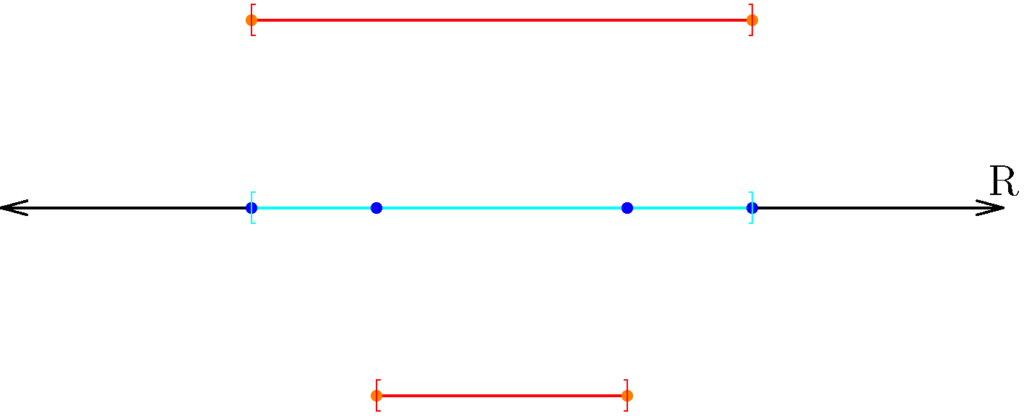
Figure 4: With unions of closed intervals, we also have three possibilities to consider. The individual intervals are colored red, while the union is colored cyan. Here, we want to pay attention to the boundary points, which are colored orange for the individual closed intervals, and blue for the union. Notice that in any union, limit points in component intervals are still limit points for the union. However, as the union grows larger, it may acquire new limit points that are not in any of the constituent intervals.
Theorem 3
Suppose is a finite collection of closed sets. Then,
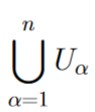
is a closed set.
General Strategy: We can use DeMorgan’s Laws to find the complement of this set, which will be a finite union of open sets. By the first theorem on this page, that union will also be open, hence, it’s complement (this set) will be closed by the topological definition of closed set.
Each Uɑ ∈ is closed, hence, (Uɑ)C is open. By DeMorgan’s Laws, we have that
.
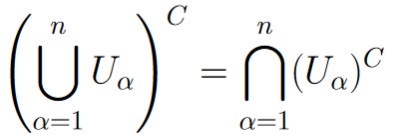By the second theorem on this page, since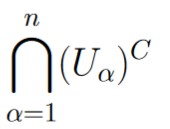 
is a finite intersection of open sets, it must itself be an open set.
Appealing to the topological definition of closed set, it must be the case that
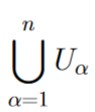
is closed as desired.
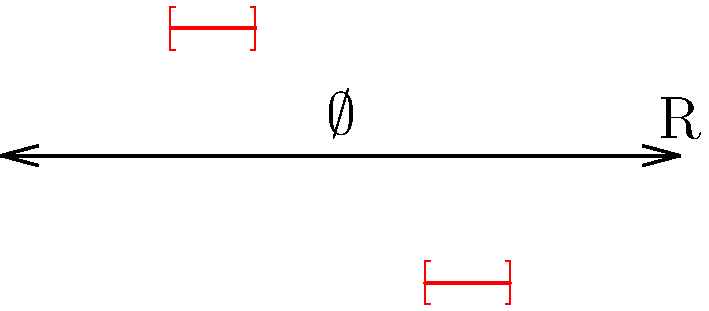
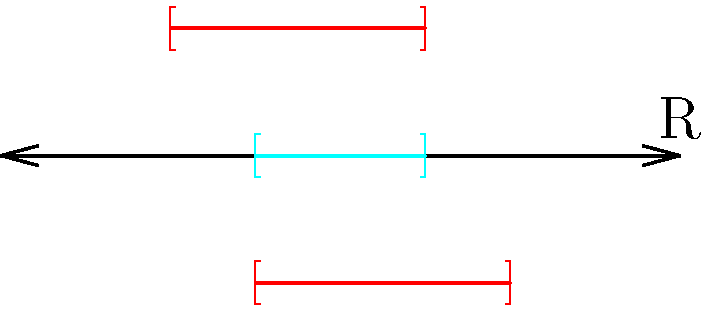
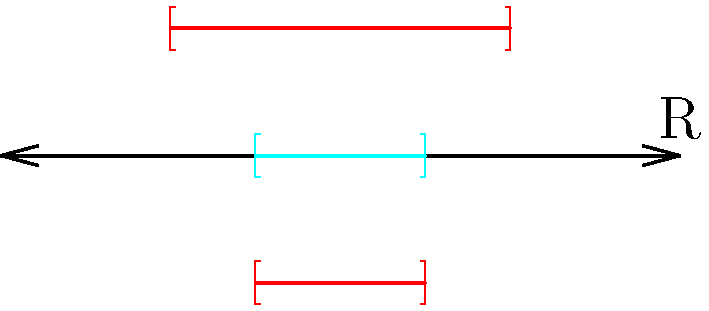
Figure 5: With intersections of closed intervals, we also have three possibilities to consider. The individual intervals are colored red, while the union is colored cyan. Here, we want to pay attention to the boundary points, which are colored orange for the individual closed intervals, and blue for the union. Notice that in any intersection, limit points in constituent intervals are still limit points for the intersection. Notice that any intersection will not gain any limit points that are not in any of its constituent intervals.
Theorem 4
Suppose {Uɑ} is a (possibly infinite) collection of closed sets where ɑ is an element of some index set I. Then,
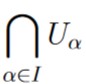
is a closed set.
General Strategy: Much like in the previous proof, we’ll use the fact that an arbitrary union of open sets is open. The connection between an arbitrary union of open sets, and an arbitrary intersection of closed sets will be made using DeMorgan’s Laws.
Each Uɑ ∈ {Uɑ} is a closed set, so by the topological definition of closed set, we have that (Uɑ)C is an open set.
By DeMorgan’s Laws, we have that
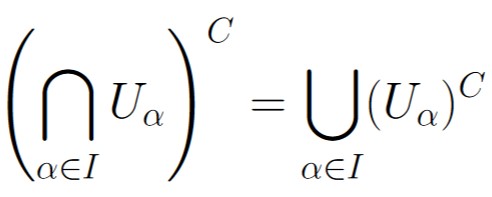
is an open set.
Notice that this is an arbitrary union of open sets, which is guaranteed to be an open set by the first theorem on this page.
Therefore, since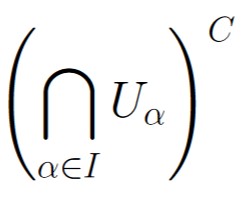 
is an open set, 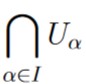must be a closed set (according to the topological definition of closed set) as desired.
Infinite Unions of Closed Sets
Again, we have a theorem regarding a finite collection of sets. Specifically, our third theorem only guarantees that finite unions of closed sets are closed. Let’s look at some examples of infinite unions of closed sets.
Example 3
One quick example of an infinite union of closed sets is
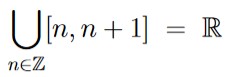
Since ℝ is open, we have that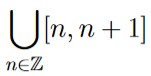 
must also be open.
Example 4
In order to generate a set that is not closed, we need to exclude a limit point. This provides an interesting opportunity to use our knowledge of convergent sequences.
For example, even though
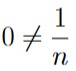
for all natural numbers n, we still have that
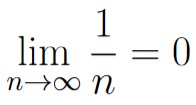
which is precisely the behavior we want: a sequence of numbers with a limit that is not in the sequence itself. Using this to guide us in our construction, we might come up with
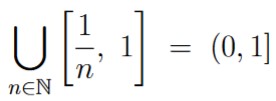
which is definitely not closed because it excludes 0, a limit point for the set.
