Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
[latexpage]
The Limit Superior and Limit Inferior of a Sequence
When a sequence converges, all of it’s subsequences converge to the same limit of the overall sequence. However, even if a particular sequence does not converge, it could still have convergent subsequences. For example, if the sequence is bounded, then the Bolzano-Weierstrass Theorem guarantees the existence of at least one convergent subsequence.
We can take this opportunity to investigate the limiting behavior of sequences that don’t necessarily converge, and in particular, we’ll look at two special types of limiting behavior that can help us characterize sequences.
Introductory Problems
Problem 1
Consider the following sequence:
\begin{equation}
a_n =
\left\{
\begin{array}{lr}
1 + \frac{1}{n}, & n \text{ is odd}\\
\frac{1}{2} – \frac{1}{n}, & n \text{ is even}
\end{array}
\right\}
\end{equation}
- Plot $ \{ a_n \}_{n = 1}^{\infty} $.
- What kind of limiting behavior does this sequence exhibit?
- Calculate sup($ \{ a_n \}_{n = 1}^{\infty} $), sup($ \{ a_n \}_{n = 2}^{\infty} $), sup($ \{ a_n \}_{n = 3}^{\infty} $), and sup($ \{ a_n \}_{n = 4}^{\infty} $).
- Does the sequence $\{\text{sup}(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$ converge? If so, to what value. If not, why not?
- Calculate inf($ \{ a_n \}_{n = 1}^{\infty} $), inf($ \{ a_n \}_{n = 2}^{\infty} $), inf($ \{ a_n \}_{n = 3}^{\infty} $), and inf($ \{ a_n \}_{n = 4}^{\infty} $).
- Does the sequence $\{\text{inf}(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$ converge? If so, to what value. If not, why not?
Problem 2
Consider the following sequence:
\begin{equation}
a_n =
\left\{
\begin{array}{lr}
n, & n \text{ is odd}\\
0, & n \text{ is even}
\end{array}
\right\}
\end{equation}
- Plot $ \{ a_n \}_{n = 1}^{\infty} $.
- What kind of limiting behavior does this sequence exhibit?
- Calculate sup($ \{ a_n \}_{n = 1}^{\infty} $), sup($ \{ a_n \}_{n = 2}^{\infty} $), sup($ \{ a_n \}_{n = 3}^{\infty} $), and sup($ \{ a_n \}_{n = 4}^{\infty} $).
- Does the sequence $\{\text{sup}(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$ converge? If so, to what value. If not, why not?
- Calculate inf($ \{ a_n \}_{n = 1}^{\infty} $), inf($ \{ a_n \}_{n = 2}^{\infty} $), inf($ \{ a_n \}_{n = 3}^{\infty} $), and inf($ \{ a_n \}_{n = 4}^{\infty} $).
- Does the sequence $\{\text{inf}(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$ converge? If so, to what value. If not, why not?
End Behavior of a Bounded Sequence
Even if a particular sequence does not converge, we may be able to identify and work with some of it’s subsequential limits. Every infinite sequence can admit many subsequences, all with their own limiting behavior. If we consider the set of all subsequential limits, we’d like to be able to describe it’s range of values.
Example 5.1
Consider the sequence
$ a_n = \{sin(\frac{n\pi}{2})\}_{n = 0}^{\infty}$
We can evaluate this sequence at the first few values (starting at n = 0) to get
0, 1, 0, -1, 0, 1, 0, -1, 0, …
We can plot this sequence for the first 50 values, which yields the following image:
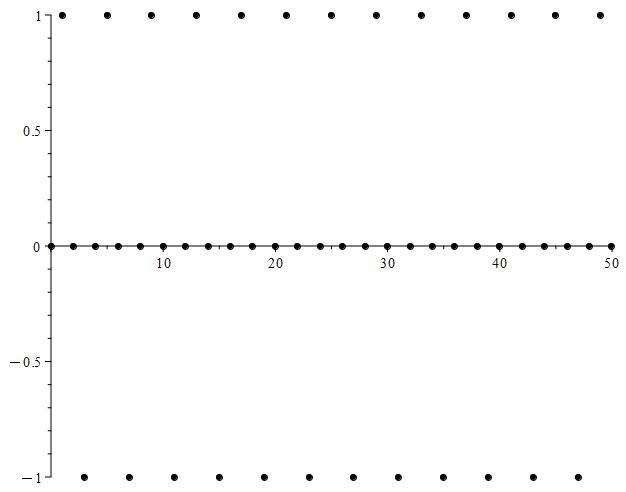
Clearly, this sequence does not have a limit, but we can still glean some useful information out of it. For example, while there is no limit per se, we can make out 3 subsequential limits, those limits being -1, 0, and 1.
We can make a subsequence that converges to 0 by simply taking all of the even indices {0, 2, 4, 6, 8, 10, …}. We can make a subsequence that converges to 1 by taking all terms with the indices {1, 5, 9, 13, 17, 21, …}, and we can form a subsequence that converges to -1 by taking all terms with indices {3, 7, 11, 15, 19, 23, …}.
Of these, 1 is the largest subsequential limit, and -1 is the smallest subsequential limit.
Just as maximums and minimums allow us to describe how “wide” a range of values can be, and how suprema and infima allow us to describe the bounds of a set of real numbers, we can use the largest subsequential limit and the smallest subsequential limit to describe how “spread out” a sequence becomes as the index tends towards infinity.
In order to see what the maximum and minimum subsequential limits are, we need can examine the supremum and infimum respectively as we restrict more and more terms from the start of the sequence. Doing this allows us to see how “big” and “small” the sequence gets as n tends towards infinity.
Solution 1.1, 1.2
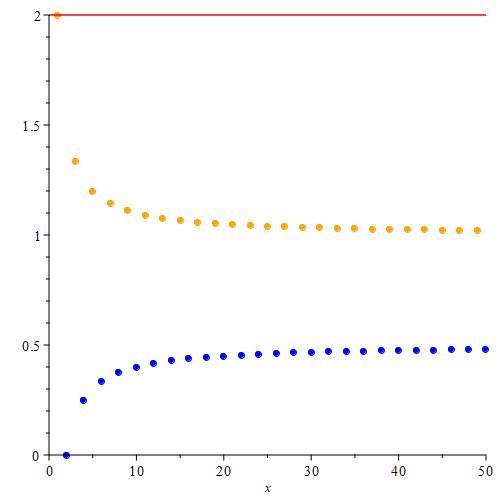
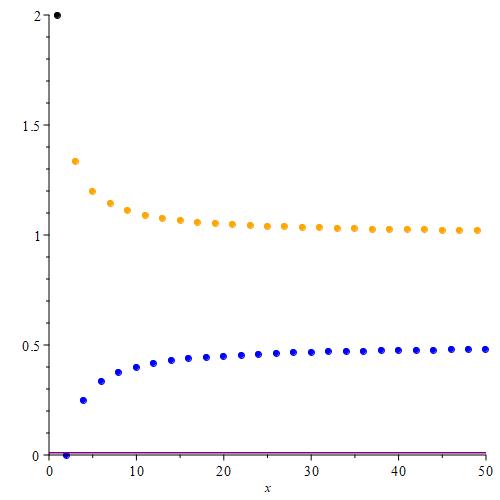
We can plot the first fifty terms of this sequence to get an idea of what is happening.
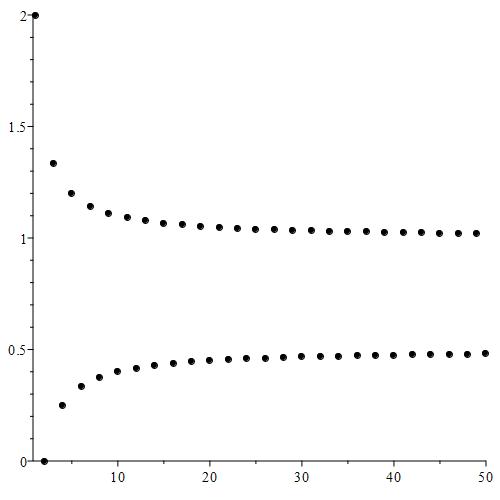
As we can see, it looks like this sequence is made up of two separate sequences, which makes sense seeing as how the given sequence is piecewise defined using two separate functions. We can color code each point corresponding to which piece generated it.
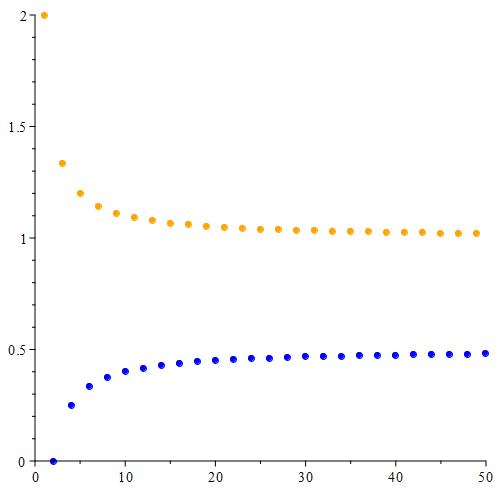
It looks like while the sequence itself has no limit as n tends towards infinity. We can make out two distinct asymptotes, those being y = 1, and y = 0.5. Indeed, evaluating the limits of each function in the definition of our sequence yields those two values.
Introducing the Limit Superior and Limit Inferior
According to the Cauchy Criterion, if we are able to bound the distance between any two terms of a sequence by any arbitrary amount – by picking a suitably large index – then the sequence converges. Essentially, what this means is that – past some index – if the upper bound and lower bound are arbitrarily close to each other, the sequence converges. The tools we have to analyze upper bounds and lower bounds of sets of real numbers are the supremum and infimum.
We can look at what happens to the infimum and supremum as we start at the beginning of the sequence, and then progressively increase the index where we take the infimum and supremum. For example, we’ll take the supremum of the entire sequence. Next we’ll exclude the first term, and then calculate the supremum. Afterwards, we’ll exclude the first two terms, then the first three, and so on. What will end up happening is that we form a sequence of suprema and infima. Just as with any other sequence, we can examine those sequences using previously developed convergence criteria.
Solution 1.3, 1.4
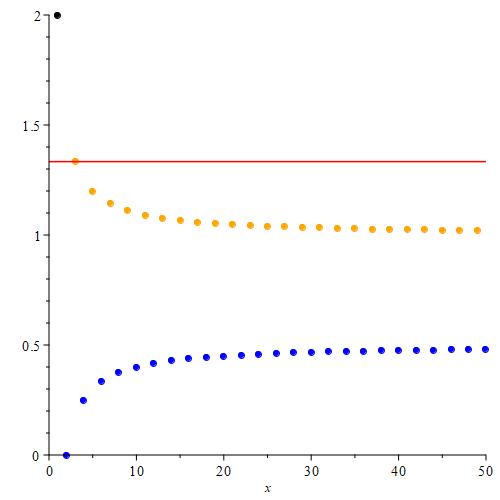
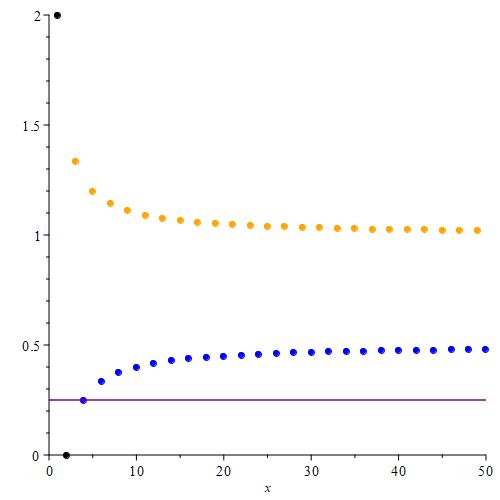
Calculating the first few suprema is relatively straight-forward for a couple of reasons. First, since we are looking at upper bounds, we can essentially ignore all of the terms associated with the second function in the piecewise-defined sequence. Those are the terms colored blue as plotted in the solution to problem 1.1. Next, if we observe that the points associated with the first function (the orange points in the plot given for solution 1.1) form a monotonically decreasing sequence, then the maximum value of the sequence will just be the orange point with the smallest index. Finally, because a supremum is just the least upper bound, and the maximum is included in the set, the supremum will be equal to the maximum value.
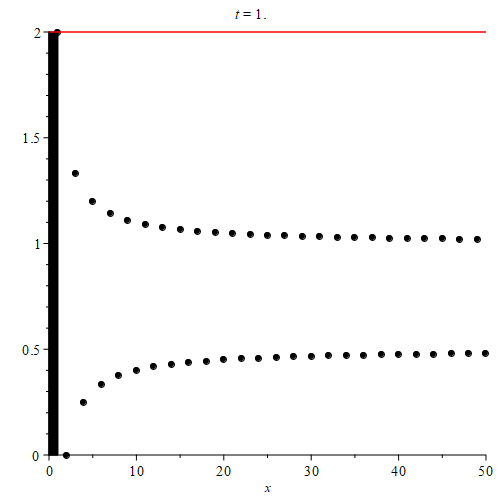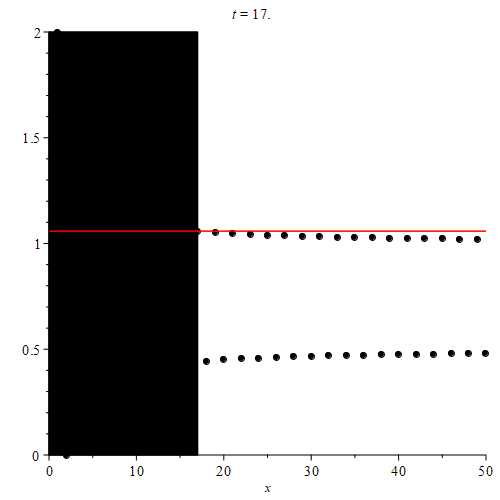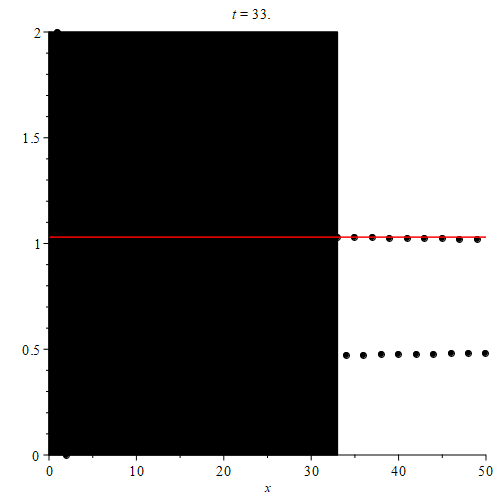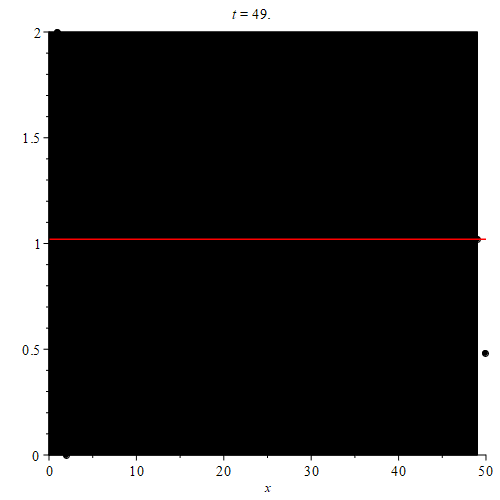
To calculate $\text{sup}(\{ a_n \}_{n = 1}^{\infty})$, start with the entire sequence, and note where the maximum is. This will be the first term of the sequence since it is the maximum value of the sequence.
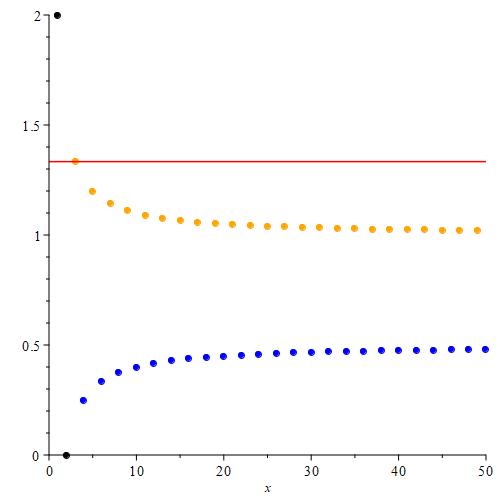
Next, we can color the first point black to signify that it is being excluded from our supremum operation. Then, to calculate $\text{sup}(\{ a_n \}_{n = 2}^{\infty})$, we simply look for the orange point with the smallest index as before. Notice that because we excluded the black point (which was originally orange), the new orange point point we’re looking for has index 3.
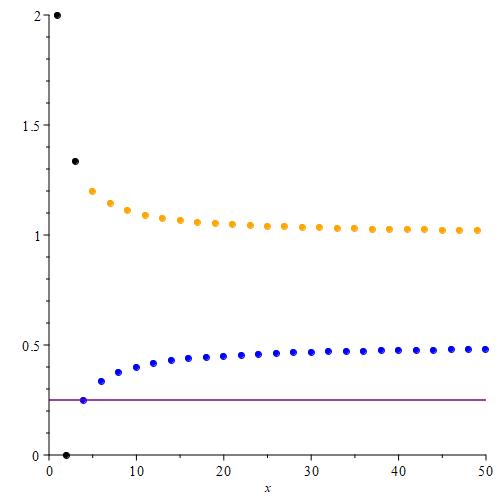
After that, we color the point with index 2 black as well. This signifies that the terms with indices 1 and 2 are now being excluded. Just as before, we still look for the orange point with the smallest index. This will be the value of $\text{sup}(\{ a_n \}_{n = 3}^{\infty})$. This time, we colored a blue point black, so the supremum was unaffected.
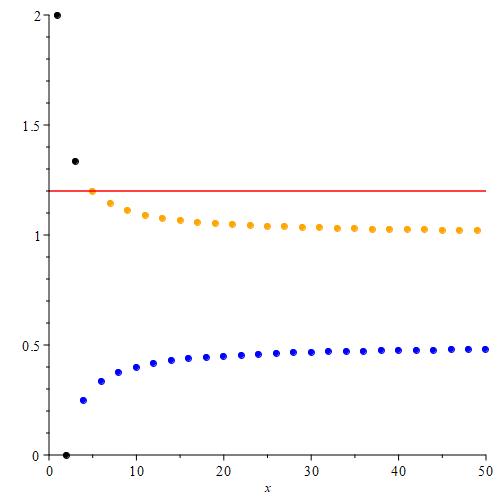
Finally, we color the point with index 3 black, signifying that the terms with indices 1, 2, and 3 are being excluded from the supremum operation. This was an orange point, so now the orange point with smallest index has index 5. This will be the value of $\text{sup}(\{ a_n \}_{n = 4}^{\infty})$.
So, we have the following:
sup($ \{ a_n \}_{n = 1}^{\infty} $) = 2
sup($ \{ a_n \}_{n = 2}^{\infty} $) = $\frac{4}{3}$
sup($ \{ a_n \}_{n = 3}^{\infty} $) = $\frac{4}{3}$
sup($ \{ a_n \}_{n = 4}^{\infty} $) = $\frac{6}{5}$
As we exclude more and more points, the supremum seems to be approaching the number 1. Seeing as the supremum is just taking the value of the largest orange point, this is not surprising.
To be somewhat more formal, note that for all $ n \in \mathbb{R}^+ $, we have that
$ 1 + \frac{1}{n} > \frac{1}{2} – \frac{1}{n}$
So, the sequence of suprema will be
$\bigstar = \{ 2, \frac{4}{3}, \frac{4}{3}, \frac{6}{5}, \frac{6}{5}, \frac{8}{7}, \frac{8}{7}, \ldots \}$
Because the sequences $\{1 + \frac{1}{n}\}_{n = 1}^{\infty}$ and $\{1 + \frac{1}{n+1}\}_{n = 1}^{\infty}$ both converge to 1, and because $1 + \frac{1}{n+1} <= \bigstar <= 1 + \frac{1}{n}$ for all $n \in \mathbb{N}$, the Sandwich Theorem guarantees that $\bigstar$ converges to 1 as well.
The value to which the suprema converge is known as the limit superior of the sequence. Of course, the limit inferior of a sequence is analogously defined.
The limit superior of a sequence $\{a_n\}_{n = 1}^{\infty}$, written $\textit{lim sup}\{a_n\}_{n = 1}^{\infty}$ is the limit \[\lim_{k \to \infty} \text{sup}\{a_n\}_{n = k}^{\infty}\]
The limit inferior of a sequence $\{a_n\}_{n = 1}^{\infty}$, written $\textit{lim inf}\{a_n\}_{n = 1}^{\infty}$ is the limit \[\lim_{k \to \infty} \text{inf}\{a_n\}_{n = k}^{\infty}\]
Solution 1.5, 1.6
We can use the same reasoning as in the solution to problem 1.3. This time, we need to use the points generated by the $\frac{1}{2} – \frac{1}{n}$ piece of the sequence because we are examining infima, or least lower bounds, of the sequence. The least lower bounds of the sequence are produced by that piece of the sequence.
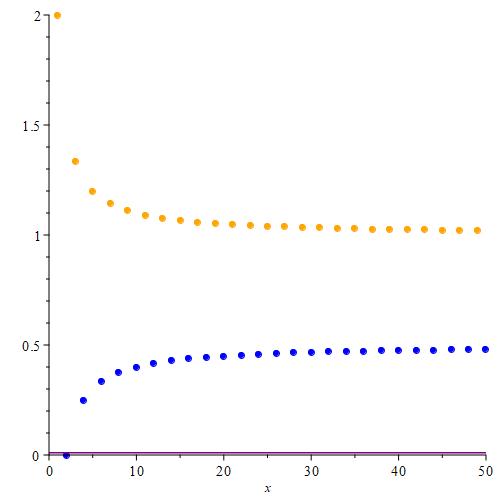
Accordingly, we have that
inf($ \{ a_n \}_{n = 1}^{\infty} $) = 0
inf($ \{ a_n \}_{n = 2}^{\infty} $) = 0
inf($ \{ a_n \}_{n = 3}^{\infty} $) = $\frac{1}{4}$
inf($ \{ a_n \}_{n = 4}^{\infty} $) = $\frac{1}{4}$
Just as we were able to sandwich (or squeeze) the sequence of suprema between two sequences converging to 1, we can do the same for the sequence of infima using two sequences that converge to $\frac{1}{2}$. The sequence of infima thus converges to $\frac{1}{2}$.
Sequences may fail to converge, so it should come as no surprise that the limit superior or limit inferior of a sequence may fail to exist. If the sequence is unbounded above, then the supremum of the sequence is at infinity. This means that limit superior is at infinity as well because in trying to form a sequence of suprema, each term of that sequence will just be infinity.
When the sequence is unbounded below, then something similar will happen to the limit inferior, but it will be at infinity as well.
Solution 2
We plot the first fifty terms of the sequence.
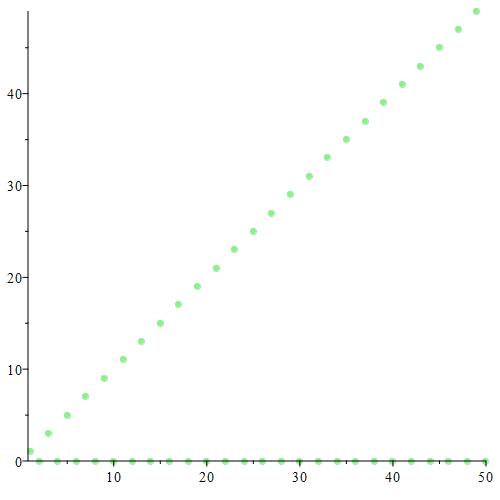
It looks like the sequence itself does not have a limit. There does appear to be a subsequence that converges to 0, but no other subsequential limits appear to exist.
Based on the definition of the sequence, one subsequence grows without bound, so no matter where we place the cut-off point for the index we start at, $\text{sup}(\{a_n\}_{n = k}^{\infty}) = \infty \text{ for all k } \in \text{ } \mathbb{N}$. Consequently, we have that $\{\text{sup}(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$ does not converge, but grows without bound. Essentially, this is just a sequence where every term is just ∞.
Turning our attention to the infimum, notice that the sequence is bounded below by 0. Indeed, one of the subsequences is just a sequence of 0s. Thus, no matter what index we start at, the infimum of the entire sequence beyond that chosen index is 0. Hence, we have that $\text{inf}(\{a_n\}_{n = k}^{\infty}) \text{ for all k } \in \text{ } \mathbb{N}$.
Furthermore, the sequence of infima converges to 0.