Properties of the Limit Superior and Limit Inferior

[latexpage]

Properties of the Limit Superior and Limit Inferior

Now that we have added the limit superior and limit inferior to our list of tools we can use to analyze sequences, we want to know exactly what kinds of information these tools yield. As discussed previously, the limit superior and limit inferior give us a way to describe how wide apart a sequence gets as its index tends towards infinity.

There are some natural questions we could initially ask. Do the sequences of suprema and infima always converge? What requirements on a given sequence guarantee convergence of the sequences of suprema and infima? What happens when the limit superior and limit inferior are equal? Here, we’ll state a few theorems and provide proofs.

An Example Sequence

Let’s take a look at another example. Suppose we were working with the sequence \[ \left\{\text{arctan}(n) + \left(\frac{1}{10}\right)\left(1 – \frac{1}{1+n}\right)\sin\left(\frac{n\pi}{2}\right)\right\}_{n = 0}^{\infty} \]

The graph of this sequence looks like it follows along the path of arctan(x), while periodically dipping above and below by a distance of $\frac{1}{10}$. As such, we can probably guess that the largest subsequential limit is roughly $\frac{\pi}{2} + \frac{1}{10}$ and that the minimum subsequential limit is roughly $\frac{\pi}{2} – \frac{1}{10}$.

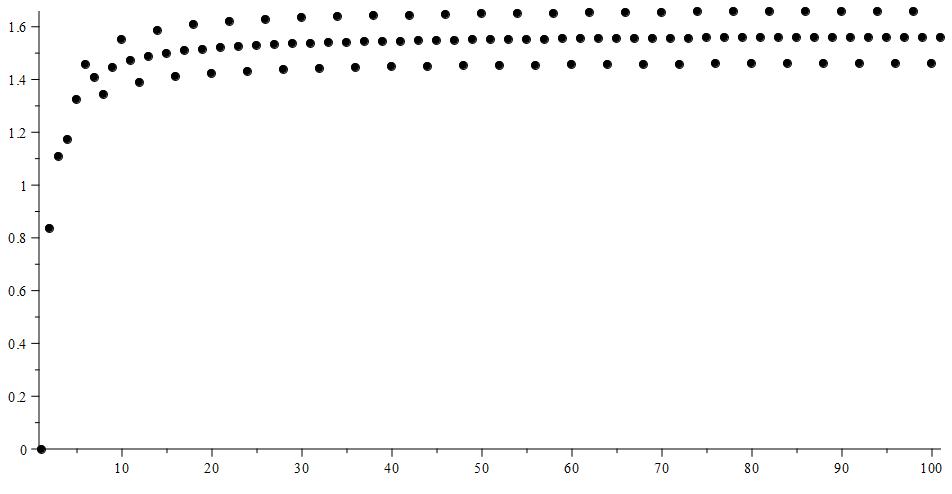
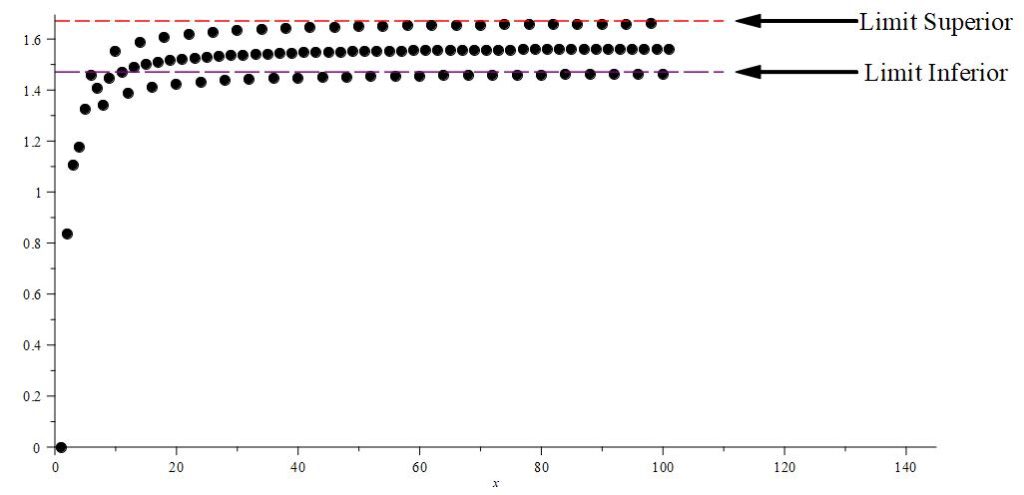
Now consider the sequences of suprema and infima that are generated by ignoring all of the starting terms. We notice that the sequence of suprema is comprised of a single value, while the sequence of infima seems to be monotonically increasing. Here, we’ll track the suprema with a red line, and the infima with a purple line.

Is it always the case that the sequence of suprema monotonically decreases? Does the sequence of infima monotonically increase? We’ll focus on properties of the sequence of suprema going forward, but the sequence of infima has analogous properties, largely for the same reasons provided.

Theorems

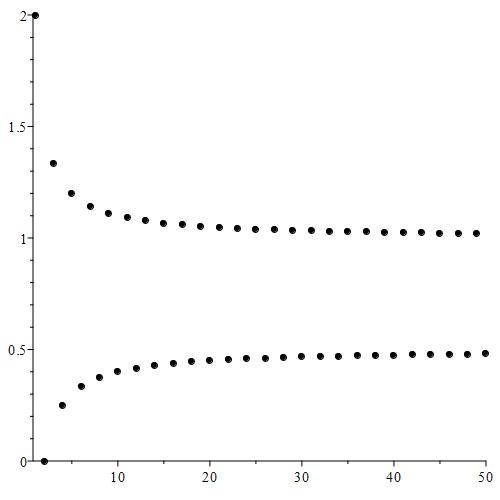
(a)

(b)

Figure 1: In (a), we see the plot for the sequence described by

This is the first sequence examined on this page of the book. In (b), we see the sequence of suprema generated by ignoring the first n terms of the sequence. Notice how the suprema seem to only decrease or stay the same.

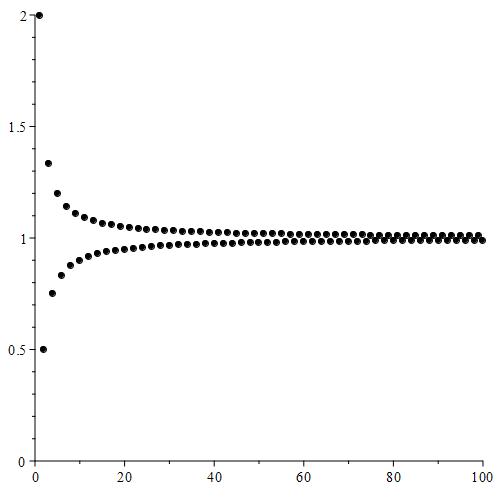
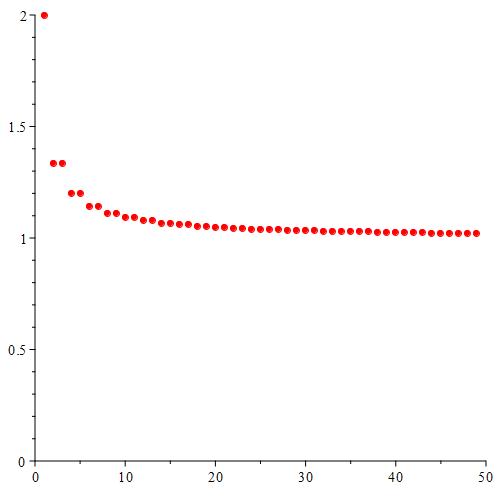
Figure 2: In the plot for the sequence

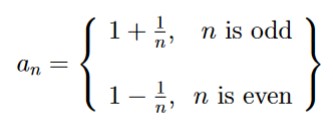
Notice that this is essentially the sequence from Figure 1, with the bottom branch pushed up. It looks like when the limit superior and limit inferior are set equal to each other, the sequence does have a limiting value.

Theorem:

Let $\{a_n\}_{n = 1}^{\infty}$ be a bounded sequence.

Then, the sequence $\{\text{sup}(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$ is a monotonically decreasing sequence, and it’s limit exists. We denote this limit as \[\lim_{k \to \infty} \text{sup}(\{a_n\}_{n = k}^{\infty})\]

Proof:

Suppose $\{a_n\}_{n = 1}^{\infty}$ is a bounded sequence.

By definition then, there exists real numbers L and U such that $\forall n \in \mathbb{N}[\text{L} \leq a_n \leq \text{U}]$.

Notice that \[ \{a_n\}_{n = 1}^{\infty} \supseteq \{a_n\}_{n = 2}^{\infty} \supseteq \{a_n\}_{n = 3}^{\infty} \supseteq \cdots \]

As a result, we must also have that \[ \sup(\{a_n\}_{n = 1}^{\infty}) \geq \sup(\{a_n\}_{n = 2}^{\infty}) \geq \sup(\{a_n\}_{n = 3}^{\infty}) \geq \cdots \]

This means that $\{ \sup(\{a_n\}_{n = k}^{\infty}) \}_{k = 1}^{\infty}$ is a monotonically decreasing sequence.

Furthermore, because $\forall n \in \mathbb{N}[\text{L} \leq a_n \leq \sup(\{a_k\}_{k = n}^{\infty})]$ the sequence of suprema $\{ \sup(\{a_n\}_{n = k}^{\infty}) \}_{k = 1}^{\infty}$ must be bounded below by L.

Therefore, because $\{ \sup(\{a_n\}_{n = k}^{\infty}) \}_{k = 1}^{\infty}$ is a monotonically decreasing sequence bounded below by L, the Monotone Convergence Theorem guarantees its convergence as desired.

This completes the proof.

Theorem:

Let $\{a_n\}_{n = 1}^{\infty}$ be a bounded sequence.

Then $\lim_{k \to \infty} \text{sup}(\{a_n\}_{n = k}^{\infty})$ equals the maximum subsequential limit of $\{a_n\}_{n = 1}^{\infty}$.

Proof:

Let $\{a_n\}_{n = 1}^{\infty}$ be a bounded sequence.

Step 1: Show that there exists subsequential limits

Let ☆ be the set of all subsequential limits of $\{a_n\}_{n = 1}^{\infty}$.

Because $\{a_n\}_{n = 1}^{\infty}$ is a bounded sequence, the Bolzano-Weierstrass Theorem guarantees the existence of at least one convergent subsequence of $\{a_n\}_{n = 1}^{\infty}$, and as a result, at least one subsequential limit exists.

In other words, ☆ ≠ ∅.

Step 2: Show that sup(☆) = max(☆)

Because ☆ ≠ ∅ and ☆ ⊆ ℝ, we have that sup(☆) exists and is in ℝ. Let α = sup(☆).

Every ε-neighborhood of sup(☆) contains some subsequential limit of $\{a_n\}_{n = 1}^{\infty}$. This means that there exists a sequence that converges to sup(☆).

This means that sup(☆) is itself a subsequential limit of $\{a_n\}_{n = 1}^{\infty}$, and so we must have that sup(☆) ∈ ☆. This means that max(☆) = sup(☆).

Step 3: Show that $\lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) \geq \alpha$

Let $x_{\infty}$ be an arbitrarily chosen subsequential limit of $\{a_n\}_{n = 1}^{\infty}$, and let $\{x_n\}_{n = 1}^{\infty}$ be an associated convergent subsequence of $\{a_n\}_{n = 1}^{\infty}$ with limit $x_{\infty}$. We can do this because ☆ ≠ ∅.

Because $\forall n \in \mathbb{N}[\sup(\{a_k\}_{k = n}^{\infty}) \geq x_n]$, we have that $\lim_{k \to \infty}\sup(\{a_n\}_{n = k}^{\infty}) \geq x_{\infty}$.

Because $x_{\infty}$ was an arbitrarily chosen subsequential limit of $\{a_n\}_{n = 1}^{\infty}$, we have that $\lim_{k \to \infty}\sup(\{a_n\}_{n = k}^{\infty}) \geq \alpha$.

Step 4: Show that $\lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) \leq \alpha$

Furthermore, because $\{\sup(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty} \to \lim_{k \to \infty}\sup(\{a_n\}_{n = k}^{\infty})$, every ε-neighborhood of $\lim_{k \to \infty}\sup(\{a_n\}_{n = k}^{\infty})$ contains some supremum of $\{a_n\}_{n = 1}^{\infty}$, and every ε-neighborhood of that supremum contains terms from $\{a_n\}_{n = 1}^{\infty}$.

This means we can construct a sequence that converges to $\lim_{k \to \infty}\sup(\{a_n\}_{n = k}^{\infty})$. This makes $\lim_{k \to \infty}\sup(\{a_n\}_{n = k}^{\infty})$ a subsequential limit of $\{a_n\}_{n = 1}^{\infty}$, and so we must have that $\lim_{k \to \infty}\sup(\{a_n\}_{n = k}^{\infty}) \leq \alpha$.

Step 5: Finishing up

Because we have both $\lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) \leq \alpha$ and $\lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) \geq \alpha$, we must have that $\lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) = \alpha$.

Ultimately, because α = max(☆), this means that $\lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty})$ = max(☆) as desired.

This completes the proof.

Theorem:

Let $\{a_n\}_{n = 1}^{\infty}$ be a bounded sequence. \[\lim_{n \to \infty} a_n \text{ exists } \Longleftrightarrow \lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) = \lim_{k \to \infty} \inf(\{a_n\}_{n = k}^{\infty})\]

In these cases, we have that \[ \lim_{n \to \infty} a_n = \lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) = \lim_{k \to \infty} \inf(\{a_n\}_{n = k}^{\infty})\]

Proof:

Let $\{a_n\}_{n = 1}^{\infty}$ be a bounded sequence.

\[ \underline{ \lim_{n \to \infty} a_n \text{ exists } \Longrightarrow \lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) = \lim_{k \to \infty} \inf(\{a_n\}_{n = k}^{\infty}) } \]

Suppose that $\lim_{n \to \infty} a_n$ exists. Call this value α.

By definition, since the limit of this sequence exists, we have that for every $\varepsilon > 0$, there exists some $N \in \mathbb{N}$ such that

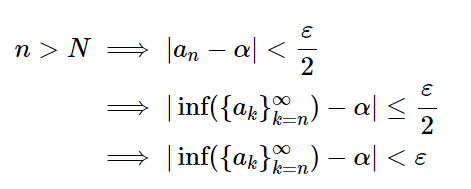
This means that the sequence of infima $\{\inf(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$ converges to α. In other words, \[ \lim_{k \to \infty} \inf(\{a_n\}_{n = k}^{\infty}) = \alpha \]

For analogous reasons, we also have that \[ \lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) = \alpha \]

Hence, we have that \[ \lim_{n \to \infty} a_n = \lim_{k \to \infty} \inf(\{a_n\}_{n = k}^{\infty}) = \lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) \] as desired.

This completes the ⇒ direction.

\[ \underline{ \lim_{n \to \infty} a_n \text{ exists } \Longleftarrow \lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) = \lim_{k \to \infty} \inf(\{a_n\}_{n = k}^{\infty}) } \]

Note that $\forall n \in \mathbb{N}[\inf(\{a_k\}_{k = n}^{\infty}) \leq a_n \leq \sup(\{a_k\}_{k = n}^{\infty})]$.

Therefore, because $\lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) = \lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty})$, the Sandwich Theorem guarantees that $\lim_{n \to \infinity} a_n$ exists, and is equal to the other two limits as well. In other words,

\[\lim_{n \to \infinity} a_n = \lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty}) = \lim_{k \to \infty} \sup(\{a_n\}_{n = k}^{\infty})\] as desired.

This completes the ⇐ direction.

With both of the ⇒ and ⇐ directions established, the proof is complete.

Theorem:

Let $\{a_n\}_{n = 1}^{\infty}$ be a bounded sequence.

\[ \lim_{k \to \infty} \text{sup}(\{a_n\}_{n = k}^{\infty}) = \inf(\{\sup(\{a_n\}_{n = k}^{\infty})\}_{n = k}^{\infty}) \]

Proof:

Let $\{a_n\}_{n = 1}^{\infty}$ be a bounded sequence. Then, the first theorem on this page guarantees the existence of $\lim_{k \to \infty}\sup(\{a_n\}_{n = k}^{\infty})$. Call this value α. Again, by the first theorem on this page, the sequence of suprema $\{\sup(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$ monotonically decreases, and converges to α.

Because $\{\sup(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$ converges to α and is monotonically decreasing, this means that $\forall n \in \mathbb{N}[\sup(\{a_k\}_{k = n}^{\infty}) \geq \alpha]$. This means that α is a lower bound for $\{\sup(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$.

Suppose β > α, then take ε = β – α > 0. Thus, because of the convergence of $\{\sup(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$, there must exist some N $\in \mathbb{N}$ such that

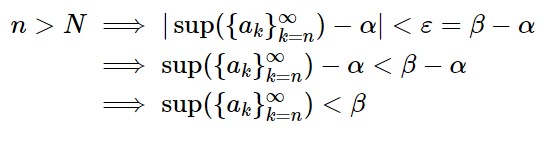
This means that no real number larger than α can be a lower bound for $\{\sup(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$.

Therefore, since α is a lower bound for all suprema, and since no number larger than α is a lower bound, we have that α is the infimum of $\{\sup(\{a_n\}_{n = k}^{\infty})\}_{k = 1}^{\infty}$.

This means that \[ \lim_{k \to \infty}\sup(\{a_n\}_{n = k}^{\infty}) = \inf\limits{n \in \mathbb{N}}(\{a_k\}_{k = n}^{\infty}) \] as desired.

This completes the proof.