Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Open Sets
The topological definition of an open set is fairly flexible. However, the open sets of a topology are typically chosen in a way that gives the notion of “closeness” or “nearness”. This is similar to, but a bit more general than, how a metric of a metric space can be used to determine how close two points are within that metric space.
In a metric space, an open set is a set that contains all of the points that are within some specified distance r of a given point p, and which also includes point p. This is exactly what is described by a neighborhood of a point in a metric space as described here.
As such, open sets give us a way to distinguish between two points. Suppose p and q are two points of some metric space. How do we know that p and q refer to two different points, or are simply two different names for the same point? One way to know is that if there is an open set containing point p that does not contain point q, then q would not be “close enough” to p to be included in the open set, and as such must be distinct from p.
For ℝ, we are going to examine what kinds of sets are open using the Euclidean metric.
Interior Points
Let’s start by picturing an example of an interval that does not include it’s left boundary point. Consider for example the interval (-5, 5], along with a small number of points.
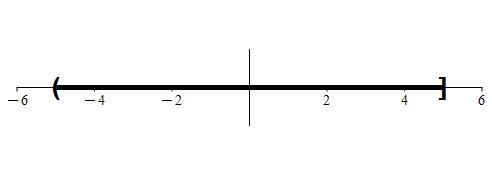
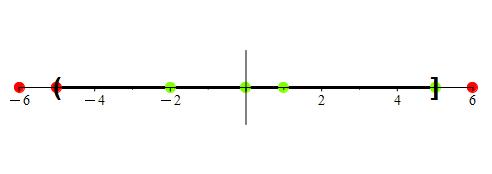
Let’s focus on four points in particular. We’ll examine the points -5, -3, 2, and 5. Here’s what we want to know: does each of these points have a neighborhood that is contained entirely within (-5, 5]? Let’s take a look at a lot of possible neighborhoods for each of these points to see if any can be found. We’ll use the variable r to designate the radius for each neighborhood.
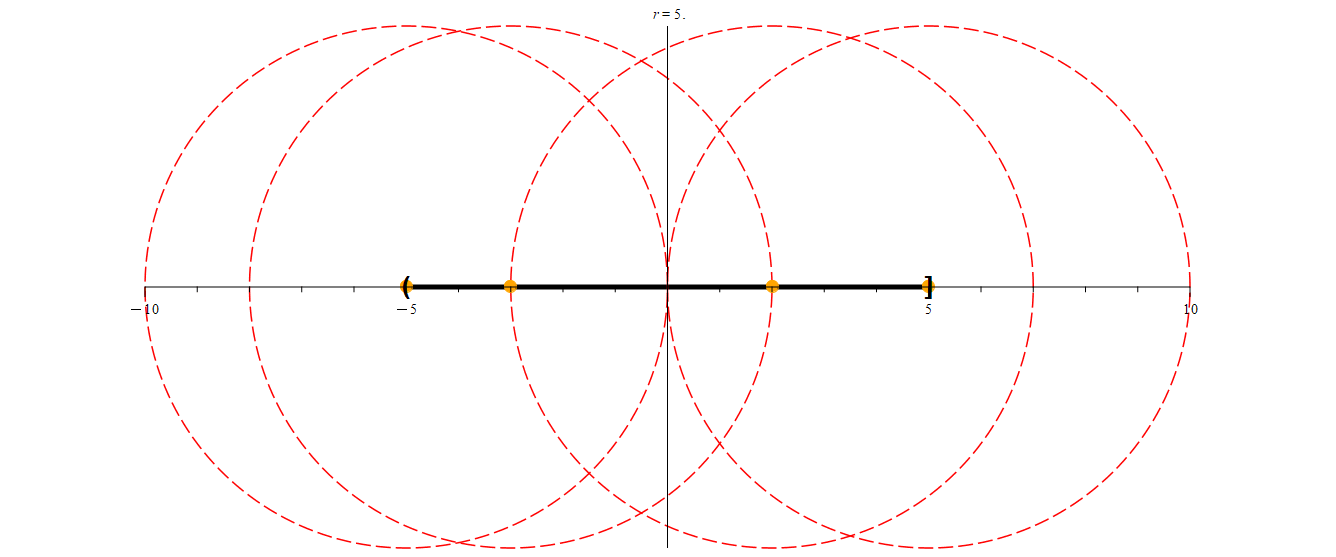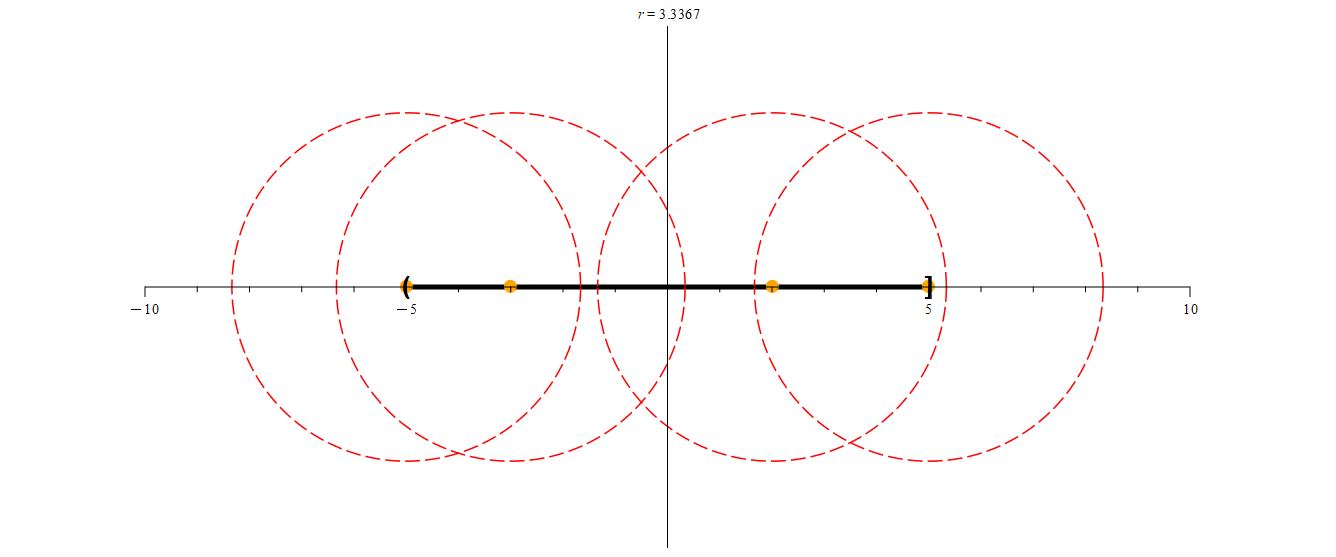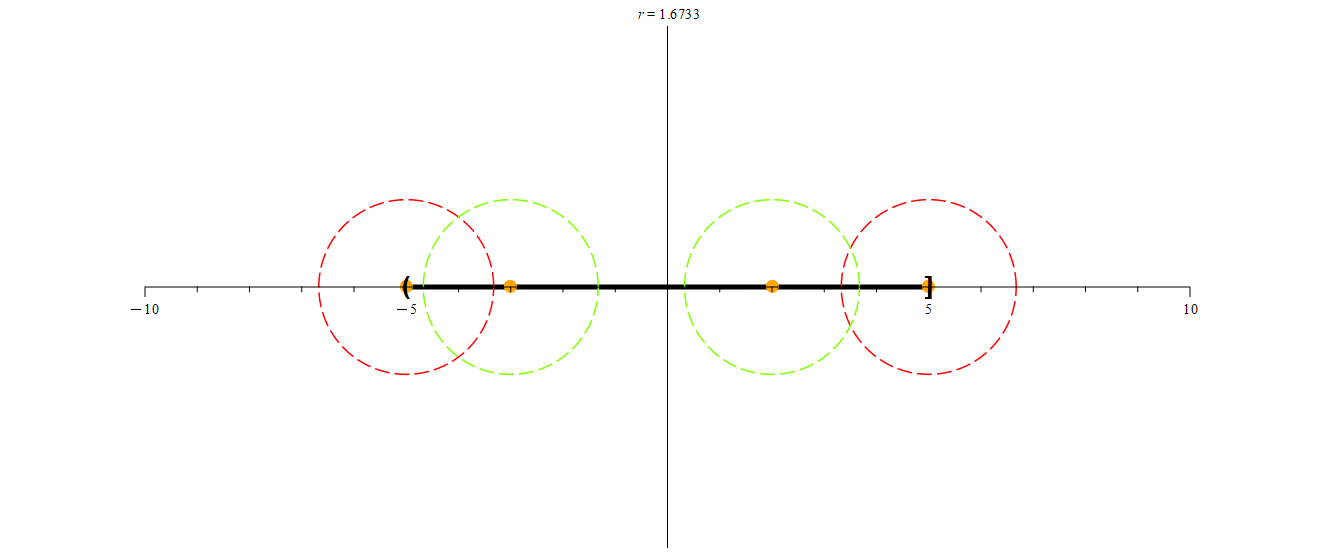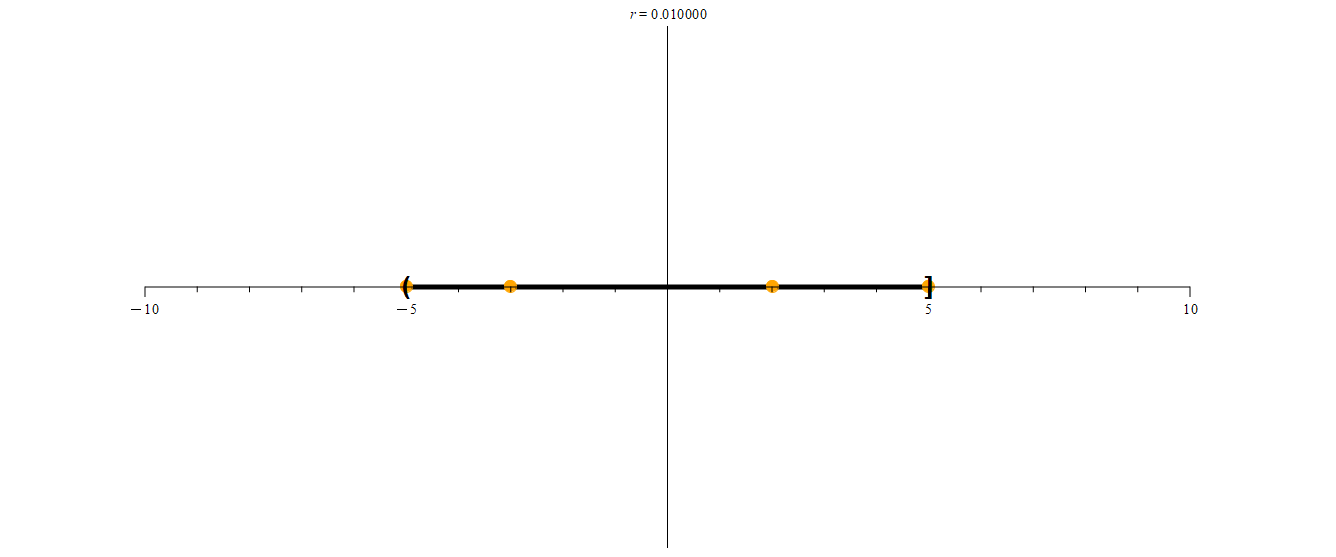
We’ll start off with neighborhoods of radius 5 for each of the orange points in the above animation. Initially, these neighborhoods will not be entirely contained within (-5, 5], so we’ll color them red. As we shrink each neighborhood, we color it green when it is contained within (-5, 5]. Notice that for -3 and 2, we can find neighborhoods that are contained entirely with (-5, 5] (in other words, they are subsets of (-5, 5].) We may notice that once we find a radius r small enough, every smaller radius will also work. However, this process seems to indicate that -5 and 5 have no such neighborhoods. Are we just not considering radii small enough to work?
Keep in mind that for any r > 0, any neighborhood of -5 with radius r will contain the point
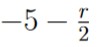
which is less than -5, and as such is not in (-5, 5], and so
Nr(-5) ⊈ (-5, 5]
no matter how small we make r. Similarly, any neighborhood of radius r for 5 will contain the point
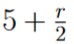
which is greater than 5, and so Nr(5) ⊈ (-5, 5] no matter how small r is.
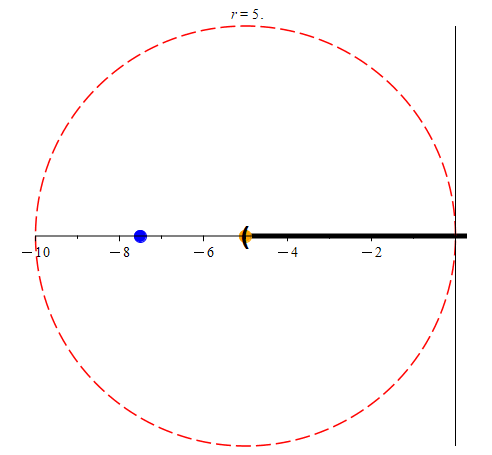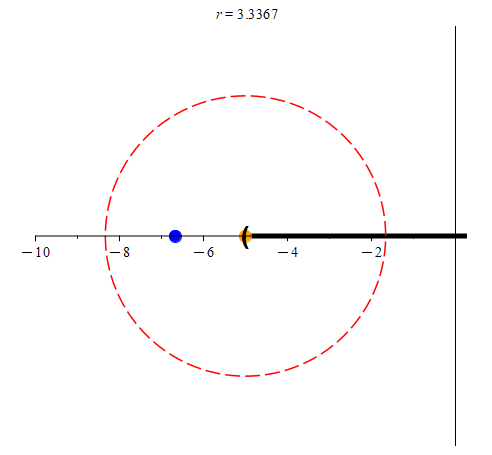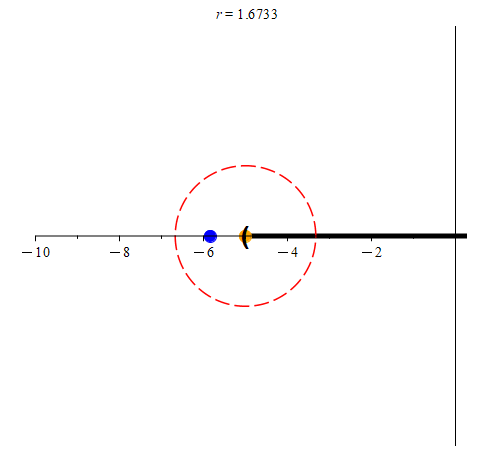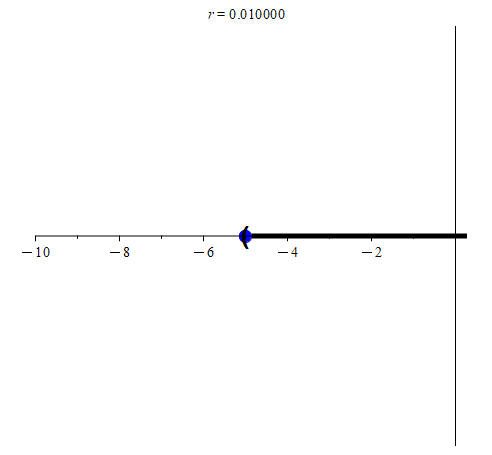
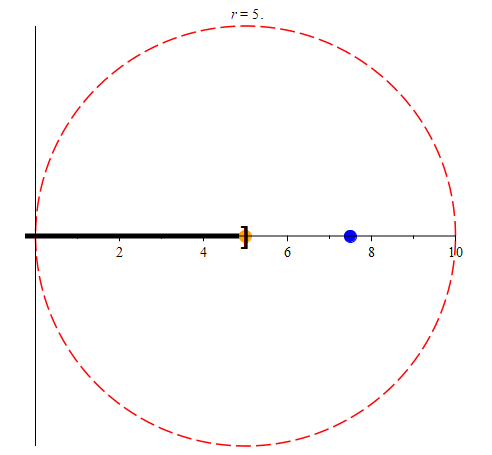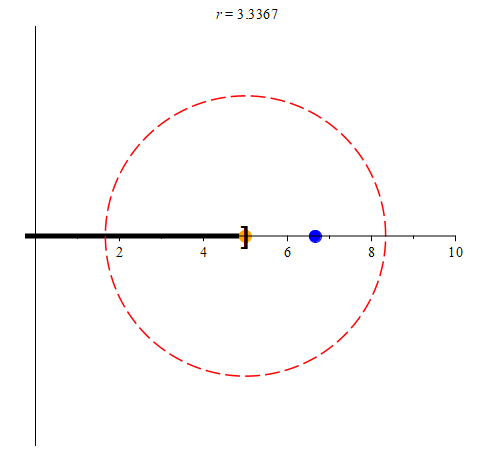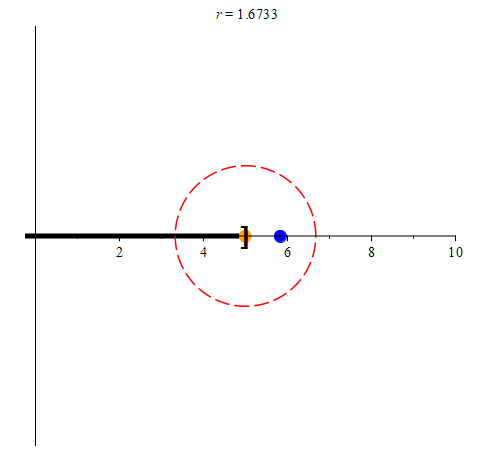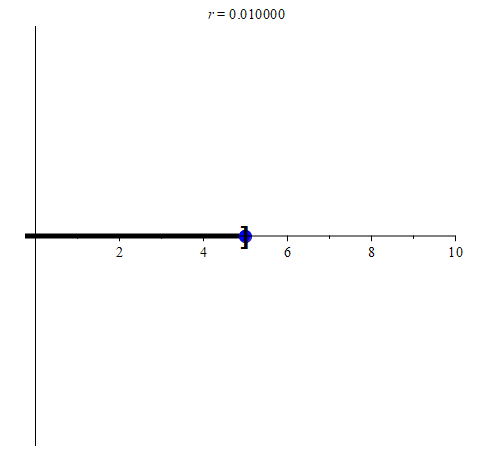
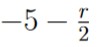(colored blue.) Notice that even though the blue point is in the neighborhood of radius r centered at -5, it is not in (-5, 5]. In the right animation, we track the point 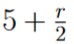(again, colored blue.) While it is also in the neighborhood of radius r centered at 5, it is not in (-5, 5]. As such, those points prevent us from being able to color the neighborhoods green.Being able to construct neighborhoods around points of a set that are entirely contained within that set is an important property for points to have.
Interior Point
Let E be a set with p ∈ E.
The point p is an interior point of E if there exists some r > 0 such that
Nr(p) ⊆ E
From Figures 1 and 2, we see that points -3, -2, 0, 1, and 2 are interior points of the interval (-5, 5], whereas -6, -5, 5, and 6 are not interior points. As a matter of fact, all of the points in (-5, 5) are interior points of (-5, 5].
Open Sets
Let’s return to Figure 2 for a moment. Notice that almost every point of (-5, 5] is an interior point. The only exception is the point 5 itself. No neighborhood of 5 will ever be a subset of (-5, 5], and as such, 5 is not an interior point.
At the other end of the interval, we see that -5 is not included in (-5, 5]. Indeed, for any points that are close to -5, we can always find a neighborhood that is a subset of (-5, 5].
N0.01(-4.9) ⊆ (-5, 5]
N0.001(-4.99) ⊆ (-5, 5]
N0.0001(-4.999) ⊆ (-5, 5]
N0.00001(-4.9999) ⊆ (-5, 5]
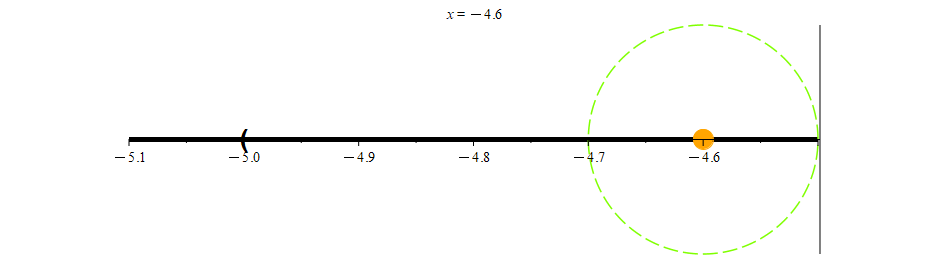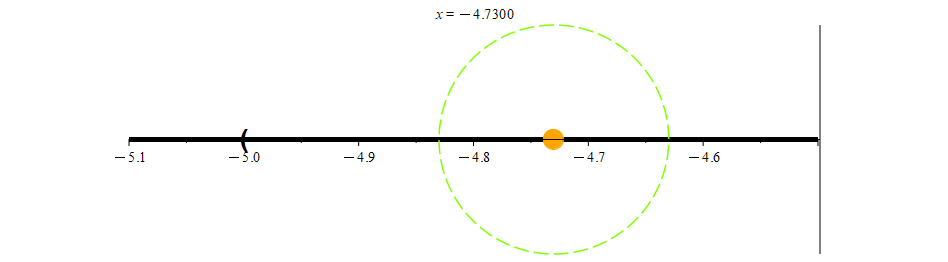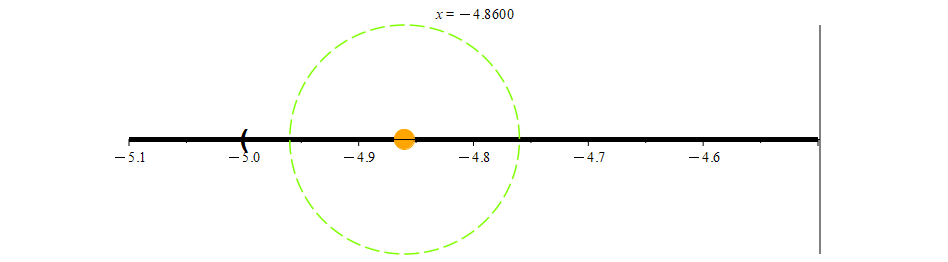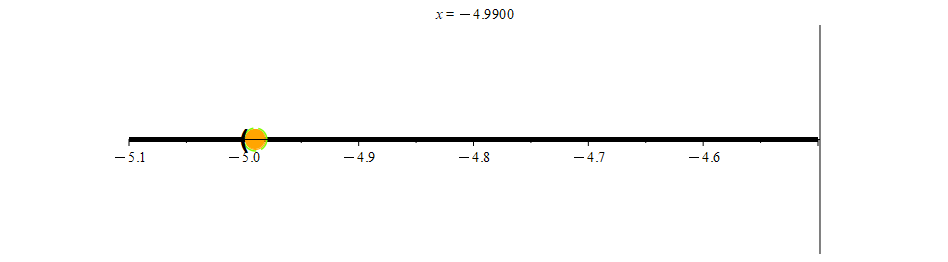
In keeping with the spirit of what an open set is supposed to be, the only point preventing (-5, 5] from being an open set is the point 5. Remembering that 5 is the only point that is not an interior point of (-5, 5], we have the following definition for open sets.
Open Set
A set E is an open set if every point of E is an interior point of E.
With that in mind, let’s toss out the point 5 from our interval, leaving us with (-5, 5), an open set. In general, any interval of the form
(a, b)
is an open subset of ℝ.
Going further, we can see that if any interval includes a boundary point, as in the following forms
(a, b]
[a, b)
[a, b]
then that interval is not open.
∅ and ℝ
Consider any point x ∈ ℝ. Because every real number is included in ℝ, any neighborhood of x will be a subset of ℝ. For example, N1(x) ⊆ ℝ. This is true of every x ∈ ℝ. Hence, we have the following.
ℝ is an open set
Now consider the empty set ∅. Is this set open? Consider that for ∅ to not be open, that means that we can find a point in ∅ that does not have a neighborhood that is a subset of ∅. Are there any such points in ∅? No, because by definition, ∅ has no points whatsoever, let alone any points with any neighborhoods not contained within ∅. Hence, ∅ must be open.
Thinking about ∅ in a different way, to say that ∅ is open is to say that every point in ∅ is an interior point of ∅. Since ∅ has 0 points, it is trivially true that all 0 points of ∅ are interior points of ∅. Hence, we make the following observation clear.
∅ is an open set
Half-infinite Intervals
There are four types of half-infinite intervals:
(-∞, a)
(b, ∞)
(-∞, a]
[b, ∞)
Based on the previous discussions involving ℝ and boundary points, we can deduce the following:
(-∞, a) and (b, ∞) are open sets
(-∞, a] and [b, ∞) are not open sets
Finite Point Sets
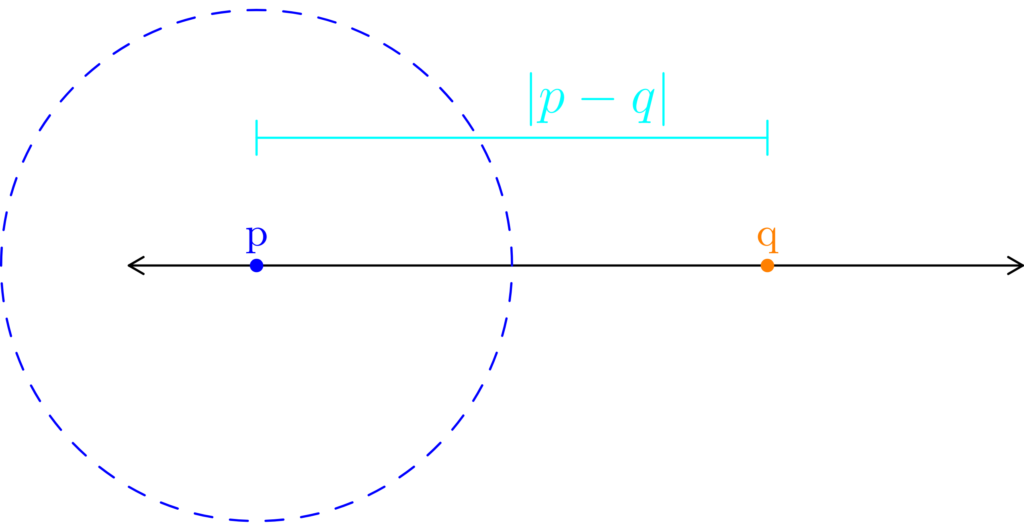
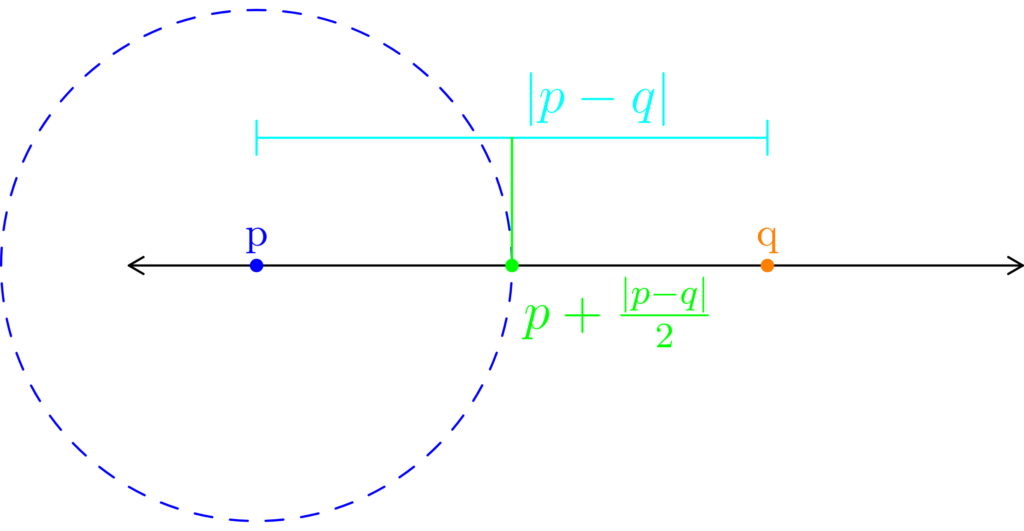
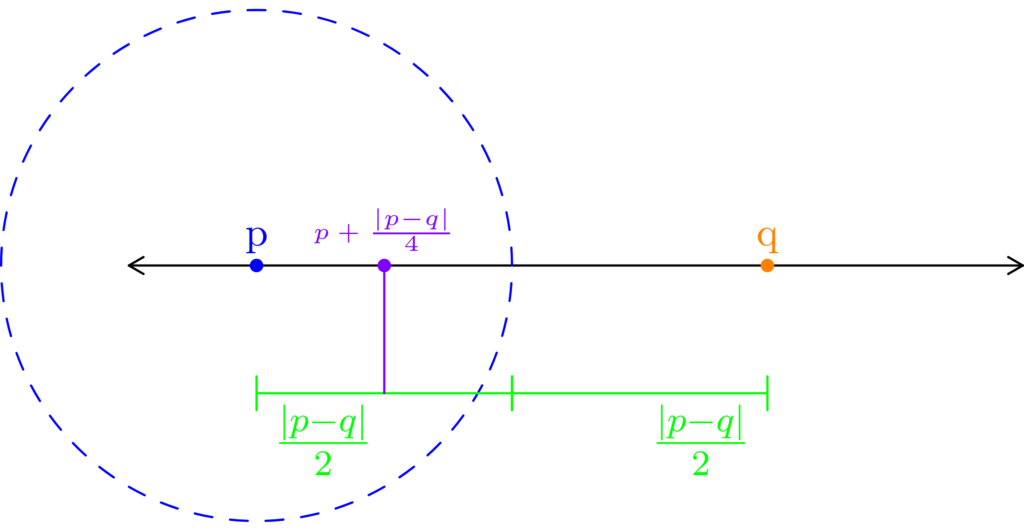
Figure 5: For any two points p and q, we can construct a neighborhood centered at p that excludes point q. As demonstrated in (a), we can just use a radius of half the distance from p to q (colored cyan.) In (b), we find the midpoint between p and q, which we’ll color green. In (c), we construct a point that half a radius to the right of p (colored purple.)
What about sets that only have a finite amount of points? We can start by thinking about sets with exactly one point.
Example 1
Is the set {0} open?
Clearly, N1(0) ⊈ {0} because 0.5 ∈ N1(0) but 0.5 ∉ {0}.
Going further, we see that for any r > 0, we have that
,
but
.
No matter how small we make r, Nr(0) ⊈ {0}. Therefore, we conclude that {0} is not open.
Example 2
Is the set {0, 0.5} open?
Based on what we saw from Example 1, clearly 0.25 ∈ N0.5(0), but 0.25 ∉ {0, 0.5} (remember that by definition of a neighborhood, 0.5 ∉ N0.5(0).)
Thus, because there is a neighborhood centered at 0 that is not a subset of {0, 0.5}, {0, 0.5} is not an open set.
We can consider what happens in Example 2 when we use two arbitrary points p and q. Consider Figure 5 below.
In Figure 5, we use cyan to denote the distance between p and q. We use light-green to construct the neighborhood centered at p whose radius is half the distance between p and q. Doing this excludes q from the neighborhood we’re constructing. Finally, we note that the purple point is in the neighborhood we just constructed, but is not in the set {p, q}.
This means we’ve constructed a neighborhood, centered at p, that is not a subset of {p, q}. We can always construct such neighborhoods between any two points. As such, two point sets are not open.
This construction can be extended to any set with a finite number of points, no matter how many points are actually in the set. Since there are only finitely many points, you can pick the two points that are closest to each other, and then follow a procedure very similar to the procedure demonstrated in Figure 5. This will yield a neighborhood that is not a subset of the original finite point set. This leads us to the following conclusion.
No finite point set is open