Metric Spaces

When working with numbers on real line ℝ, we are often interested only in a set of points that are “near” other points. For example, when working with sequences, we may want to know whether or not a sequence converges. We do this by examining how close the tail-end of a sequence gets to some point x. One way to frame this examination is in terms of distance. If we’re always able to find some index after which all terms of a sequence are within any given distance ε > 0 of a point x, then we say that sequence converges to x. The idea of a metric space generalizes the concept of distance, and will gives us tools to work with subsets of ℝ that are defined in terms of distance.

What is a Metric Space?

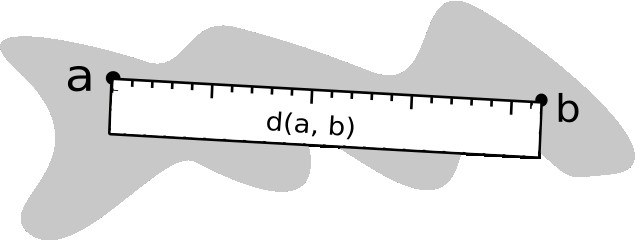
Figure 1: Consider the above set with points a and b. To say that the above set is a metric space is to say that we can figuratively place a ruler from point a to point b, and the distance function will reveal the length of the ruler.

We start by defining a metric space. The idea is that for any two points in some set, we should be able to determine the distance between them.

Metric Space, Distance, Metric

A set X is called a metric space if, with any two elements p, q ∈ X, there is a real number d(p, q) called the distance between p and q such that

d(p, p) = 0	a point is 0 distance from itself
d(p, q) > 0	the distance between two distinct points should be positive; no negative distances
d(p, q) = d(q, p)	the distance from p and q is the exact same distance from q to p
d(p, q) ≤ d(p, r) + d(r, q)	the Triangle Inequality

Any function d: X² → ℝ⁺ ∪ {0} satisfying the 4 properties above is called a distance function, or metric, for X.

For any given point x in a metric space, we may only care about other points that are within a specified distance of x. Neighborhoods give us a way to construct subsets of a metric space that consist of points as close to x as we want.

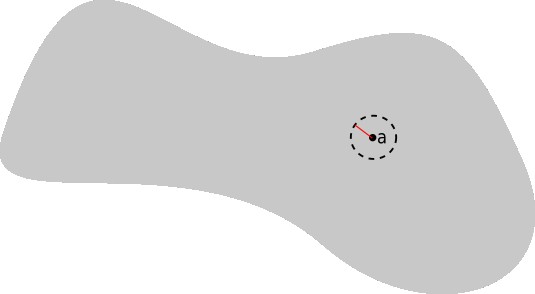
Figure 2: In the set above, a neighborhood about point a is drawn, with the radius colored red. Notice that the circle is dashed, indicating the outer edge of the circle is not part of the neighborhood.

Neighborhood, Radius

A neighborhood of p ∈ X is a set N_r(p) ⊆ X consisting of all q ∈ X such that

d(p, q) < r

for some r > 0. In set-builder notation, this would be the set

N_r(p) = {q | q ∈ X ∧ d(p, q) < r}.

The number r is called the radius of the neighborhood.

We can consider neighborhoods of any radius r > 0. Just like with sequences, being able to control how far away a certain set of points can be from the center of a neighborhood will determine several properties of that set.

ℝ as a Metric Space

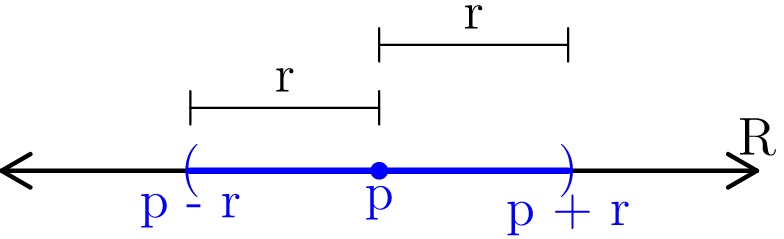
Figure 3: In (a), we see what a neighborhood in ℝ looks like when colored blue. There is a center point p, along with a radius r. In(b), we see several points in ℝ. The red points are not in N_r(p), while the green points are in N_r(p).

The metric space we’ve been working with throughout the book, and will continue working with, is ℝ along with the absolute value d(p, q) = |p – q|.

Using this metric, we see that a neighborhood of radius r, centered at point p, is the set

N_r(p) = {q | q ∈ ℝ ∧ |p – q| < r} = (p – r, p + r)

These are the segments of the form (a, b) where

a = p – r
b = p + r.

Characterizing Subsets of Metric Spaces

Consider some set E ⊆ X where X is a metric space. By virtue of the fact that that all points in E are also points of X, we have that E is also a metric space, along with the exact same metric as used by X. In our case, this means that any subset of ℝ, along with the absolute value, is itself a metric space.

As demonstrated in Figure 3, subsets of ℝ will include some points and exclude others. Here, we start to characterize such subsets, and will start to identify points of interest. First, we describe points that are either in the set, or not in the set.

Figure 4: In (a), we see some set within ℝ, colored blue here. In (b), we colored different parts of the real line depending on what part of the set it’s in. The green portion represents the set’s interior, while the red portion represents the set’s exterior. Notice that at the extreme endpoints of the blue set in (a) and (b) there are black dots. Those black dots are in neither the interior or exterior of the set depicted in (a). They represent the boundary points. In (c), we see that every neighborhood of both boundary points will always intersect both the red portion and green portion. In every neighborhood, we track a green point and a red point to make this obvious.

Interior Point, Interior

Let X be a metric space with E ⊆ X.

Suppose p ∈ E. If there exists some r > 0 such that

N_r(p) ⊆ E

then we say that p is an interior point of E.

The set of all interior points of E is called the interior of E.

Exterior Point, Exterior

Let X be a metric space with E ⊆ X.

Suppose p ∈ E^C. If there exists some r > 0 such that

N_r(p) ⊆ E^C

then we say that p is an exterior point of E.

The set of all interior points of E is called the exterior of E.

Boundary Point, Boundary

Let X be a metric space with E ⊆ X.

Suppose p ∈ X. If for all r > 0 we have that

N_r(p) ∩ E ≠ ∅ and N_r(p) ∩ E^C ≠ ∅

meaning every neighborhood centered at p intersects both E and E^C, then p is called a boundary point for E (and E^C.)

The set of all boundary points for E is called the boundary of E.

There are two other types of points that we may come across from time to time.

Figure 5: In (a), we see a subset within ℝ, colored blue. Notice that there are two dots not included in the interval that are still part of the set. In (b), we see we can draw a neighborhood (represented by a blue dashed circle) centered at each of those blue dots that do not intersect any other part of the set. Hence, they are isolated points of the set.

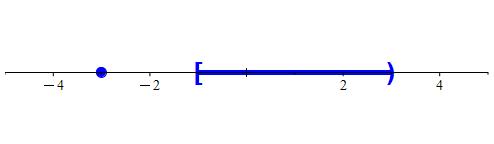
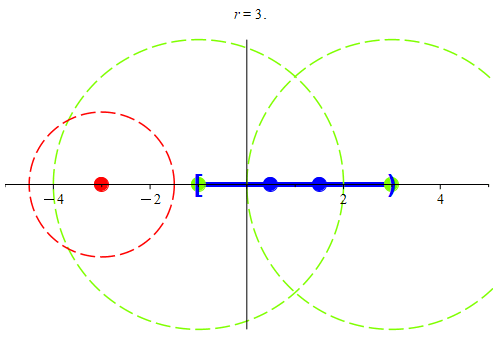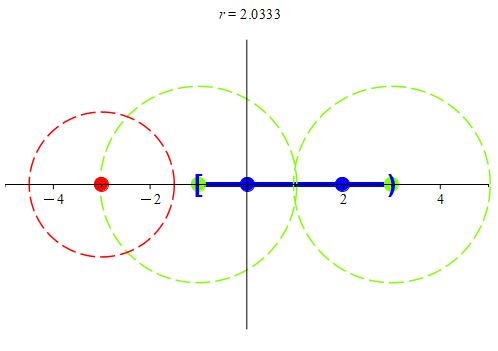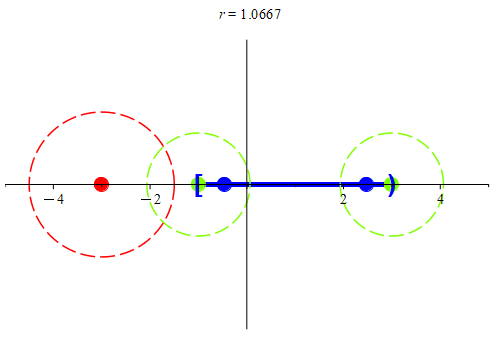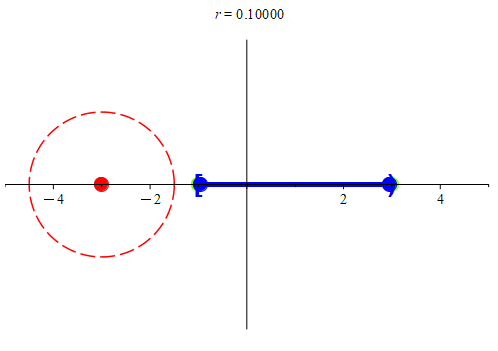
Figure 6: In(a), we a subset of ℝ, colored blue. Notice that there is an isolated point at -3. The two boundary points for this set are at -1 and 3. In (b), we see why the point at -3 is an isolated point: we found a neighborhood centered at -3 that only intersects the set at -3. We color the isolated point red for clarity. We also see that the two boundary points were colored green. We see that in every neighborhood centered at the two boundary points, there is always another point, colored blue.

Isolated Point

Let X be a metric space with E ⊆ X.

Suppose p ∈ E. If there exists some r > 0 such that

N_r(p) ∩ E = {p}

meaning, there is a neighborhood centered at p that only contains p and no other point from E, then we call p an isolated point of E.

Cluster Point, Limit Point, Articulation Point

Let X be a metric space with E ⊆ X.

Suppose p ∈ X. If for all r > 0 we have that

N_r(p) ∩ E ≠ ∅

then p is called a cluster point for E. Notice that we don’t need p ∈ E.

Other common names for this kind of point are limit point and articulation point.