Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
When trying to decide if a function achieves maximum or minimum values, or if it takes on certain intermediate values in it’s range, we’ll need to look at the structure of it’s domain. If there are any missing values, then such guarantees can not be made.
Consider the function -(x – 2)2. Looking at a graph will quickly reveal that a global maximum is achieved at x = 2. However, that is only true if the domain over which it is defined includes the value x = 2. Suppose instead we were working with the domain (-∞, 2) ∪ (2, ∞), then no global maximum is achieved. Once we split the real numbers into two disjoint subsets by removing a number, we no longer can guarantee the existence of a global maximum or minimum.
Of course, defining the function over a domain such as (-∞, 2) ∪ [2, ∞) or (-∞, 2] ∪ (2, ∞) would solve the problem. The issue basically arises because we split ℝ into two disjoint pieces that don’t share a boundary, then there are numbers in ℝ that are not represented in the function’s domain. We can concisely describe the issue here by saying that (-∞, 2) ∪ [2, ∞), (-∞, 2] ∪ (2, ∞), and ℝ are connected, while (-∞, 2) ∪ (2, ∞) is disconnected.
Suppose A and B are both non-empty subsets of some metric space X such that A ∩ B = ∅.
A and B are called separated if both
A ∩ B = ∅ and A ∩ B = ∅.
That is, if A does not contain any points from B or B’s boundary (B’s closure), and B does not contain any points from A or A’s boundary (A’s closure.)



Figure 1: All it takes for two sets to be separated is a single point missing from both.
Consider Figure 1. Pictured in (a) are two open sets A and B of the form
A = (a, x), B = (x, b).
Notice that x ∉ A and x ∉ B, but that x ∈ A and x ∈ B. In (b), we consider the closure of A along with B. Notice that because x ∈ A and x ∉ B we have that
A ∩ B = ∅.
Similarly, in (c) we see that x ∉ A and x ∈ B and so
A ∩ B = ∅.
Thus, because A ∩ B = ∅ and A ∩ B = ∅, we have that A and B are mutually separated.


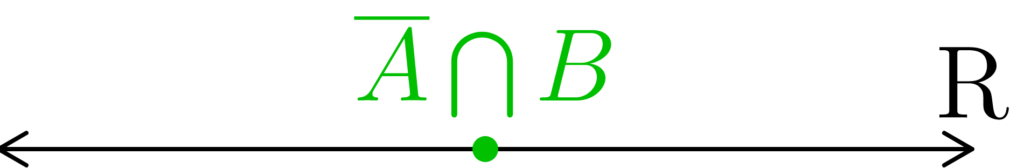
Figure 2: Once a boundary is shared between two intervals within ℝ, they are no longer mutually separated.
In Figure 2, part (a), we see that B actually has one of A’s boundary points. We have that
A = (a, x), B = [x, b).
In (b), we see that x ∈ A, and since we also have that x ∈ B, we have that
A ∩ B = {x} ≠ ∅,
and so A and B are not mutually separated.


Figure 3: Whether separated by a single point (as in part (a)), or an entire interval (as in part (b)), once both sets exclude every point of the other set’s boundary, there’s some separation between the two sets. The red points in both (a) and (b) act like barriers.
Let X be a metric space with E ⊆ X, and let A and B be separated subsets of X such that
E = A ∪ B.
E is called a disconnected set.
Based on this definition, two intervals of the form
(l, x) and (x, r)
where l < x < r are separated. Thus, if we have some set E where
E = (l, x) ∪ (x, r)
then E is disconnected.

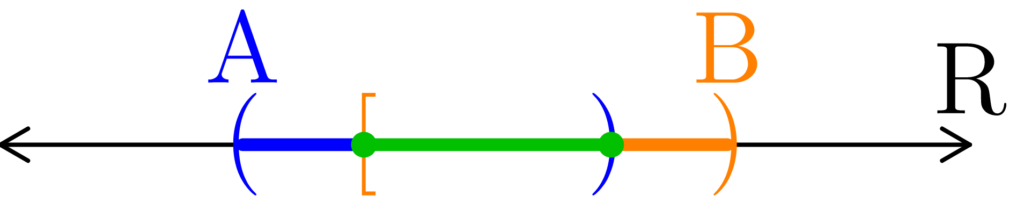
Figure 4: When there are no points separating two sets, then those sets are connected. In (a), both A and B share a single point. In (b), A and B share an entire interval of points. In both, the green points act as a bridge, or a transition, from one set to the other.
A set E ⊆ X, where X is a metric space, is called a connected set if it is not disconnected.
In other words, E is a connected set if there does not exist two separated subsets of X, A and B, such that
E = A ∪ B.
Let E ⊆ ℝ.
E is connected ⟺ If x ∈ E, y ∈ E, and x < z < y, then z ∈ E.
General Strategy: In either direction, we use an indirect approach; that is, we prove the contrapositive of each direction. Once we establish what the contrapositive is, we simply appeal to the relevant definitions.
E is connected ⟹ If x ∈ E, y ∈ E, and x < z < y, then z ∈ E
The contrapositive of the statement we’re trying to prove is
If x ∈ E, y ∈ E, x < z < y, and z ∉ E ⟹ E is disconnected.
Suppose it was the case that x ∈ E, y ∈ E, x < z < y, and z ∉ E.
Let A be the part of E that is less than z, and B be the part of E larger than z; in other words,
A = (-∞, z) ∩ E, B = (z, ∞) ∩ E.
Since A includes every number in E up to, but not including z, and B includes every real number in E greater than z, we have that
E = A ∪ B.
Also notice that since A ⊆ (-∞, z) and that B ⊆ (z, ∞), we have that A and B are separated sets.
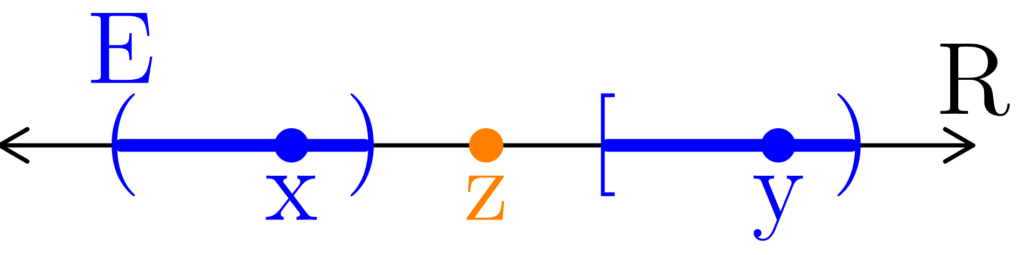
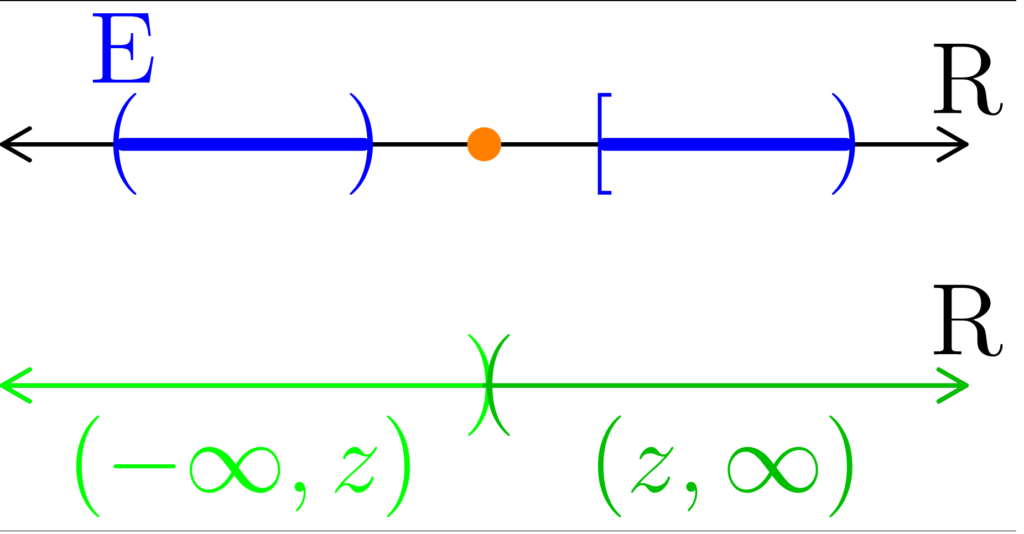
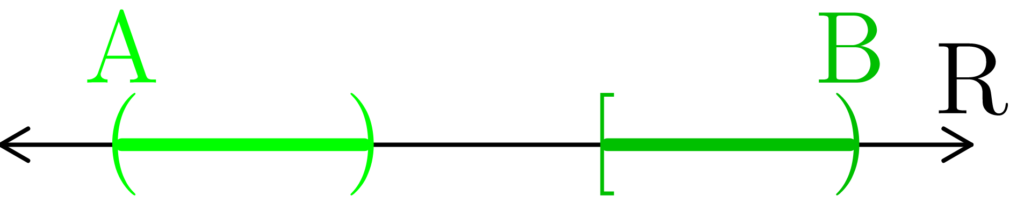
Figure 5: In (a), we show some general set E where x ∈ E, y ∈ E, x < z < y, and z ∉ E. In (b), we show what happens when we split the set apart at the point z by intersecting E with two different half-infinite open intervals. In (c), we see that, by how A and B were constructed, that E is really a union of two separated sets. Notice that B includes one of it’s boundary points. When there is an interval separating two portions of E, then boundary points can be included.
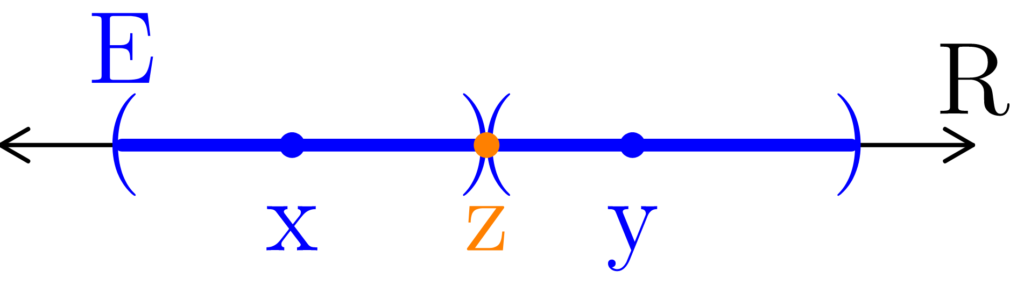
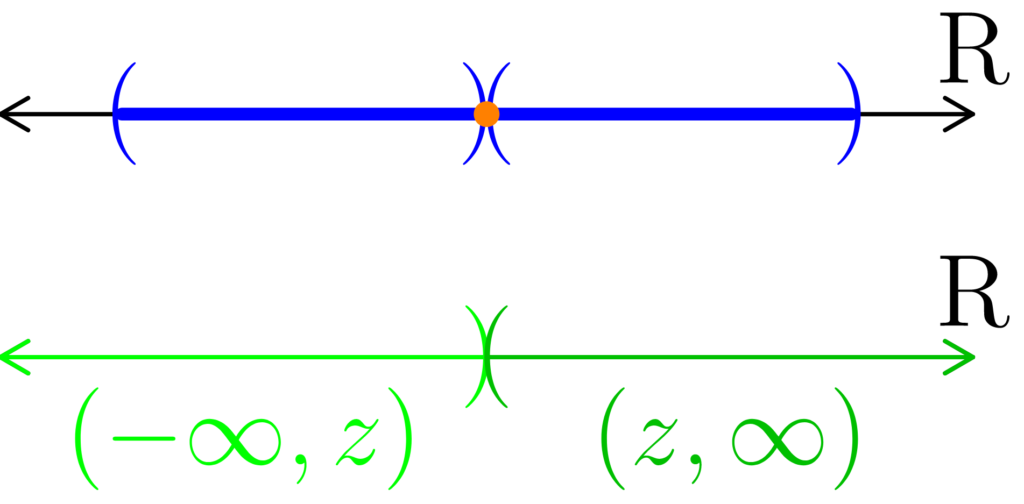

Figure 6: Just line in Figure 5, we start with a general set E, however this time, there is only a single point between both parts of E. In (a), we still have x ∈ E, y ∈ E, x < z < y, and z ∉ E. If we continue with the construction of A and B, as demonstrated in (b) and (c), we still get that E is the union of separated sets. When only a single point point separates the parts of E, then neither part can include that point as a boundary point.
Since E is equal to a union of separated sets, E must be disconnected.
This proves the contrapositive, meaning we also proved the underlined statement at the top as well.
E is connected ⟸ If x ∈ E, y ∈ E, and x < z < y, then z ∈ E
The contrapositive of this statement is
E is disconnected ⟹ x ∈ E, y ∈ E, x < z < y, and z ∉ E.
Suppose that E was disconnected. Then by definition, E is equal to the union of two separated sets; in other words; we have that
A ⊆ ℝ and B ⊆ ℝ,
A ∩ B = A ∩ B = ∅, and
E = A ∪ B.
Without loss of generality, let x ∈ A and y ∈ B such that x < y.
Let zA = sup( { a : (x, a) ⊆ A } ). This would make zA a limit point for A and a boundary point for A, so zA ∈ A. And since zA ∈ A, we have that zA ∉ B. We now need to check what happens if zA ∈ A and when zA ∉ A.
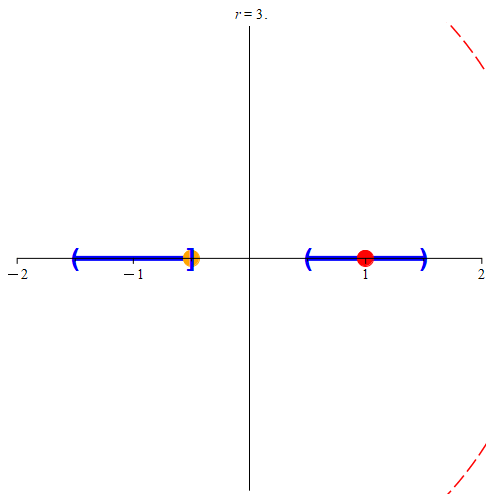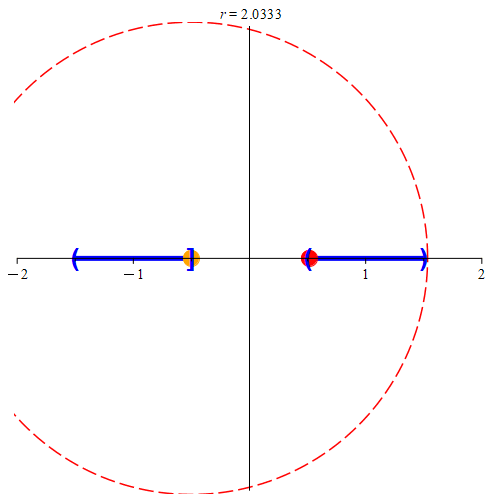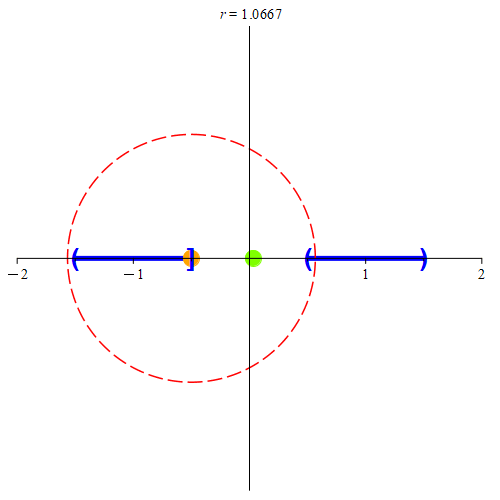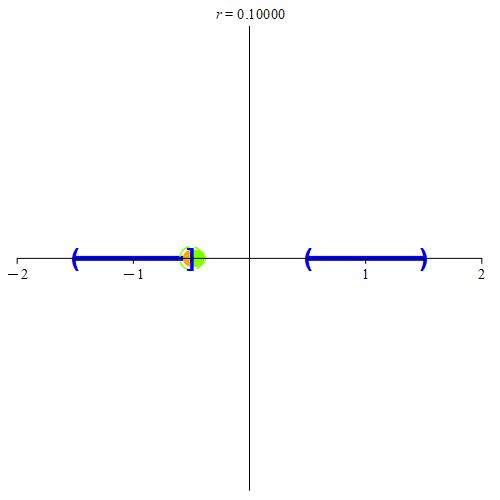
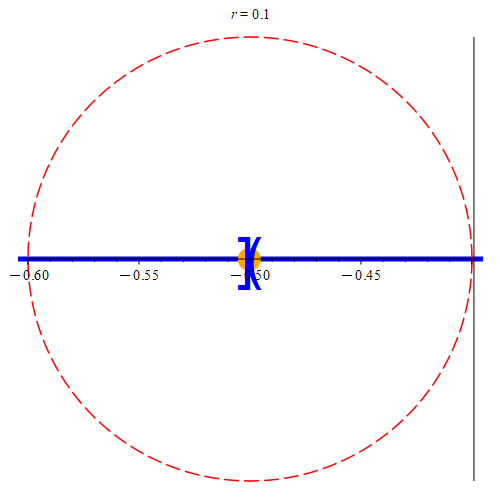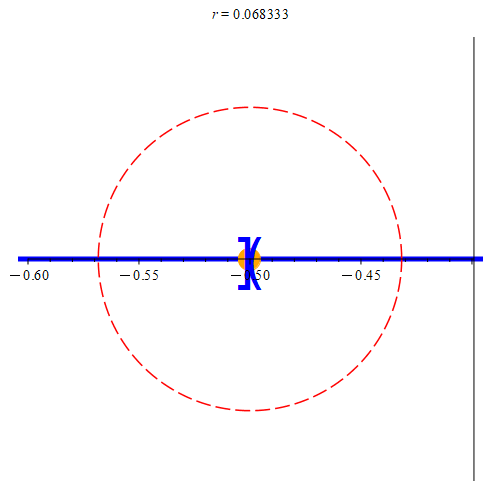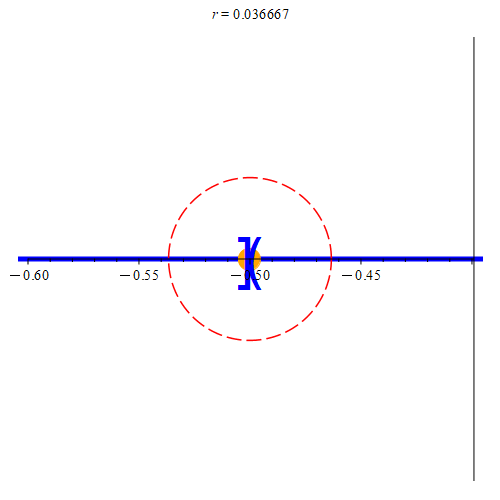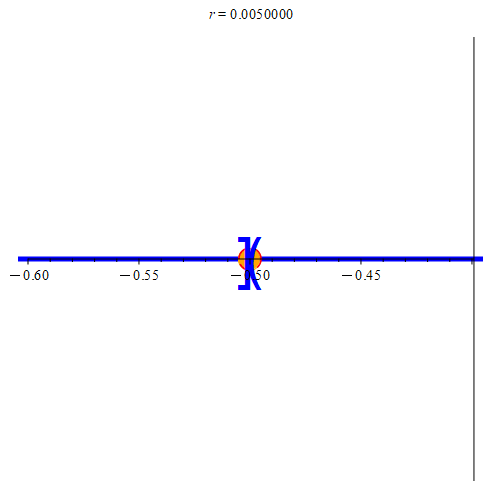
Figure 7: This is the situation when zA ∈ A. Here, zA is the orange point. The two blue sets represent A and B, where A is on the left, and B is on the right of the orange point. In (a), there is an interval separating A and B. As such, we’ll be able to find some neighborhood centered at zA that does not contain any points from B. If the neighborhood intersects B, we’ll color it red, otherwise, we’ll color it green. Once the neighborhood is small enough, we can find a point on the line that is not in A or in B. We’ll color such a point green. Notice that we can always find points not in A or B (we color the point green before the neighborhood to signify this), but until the neighborhood is small enough, we can’t guarantee that any arbitrarily picked point in the neighborhood won’t be in B. Any of the green points can be our value of z. In (b), there is no separation, and as such does not meet the requirement that E is disconnected. Note that no neighborhood is guaranteed to give us points that are not in B (in fact, no such neighborhood will give us points not in B.) Hence, the neighborhood is always colored red. As such, no value of z exists to meet our requirements.
If zA ∈ A, then since A ∩ B = ∅, we’d have that zA ∉ B, and thus by extension, zA ∉ B. Therefore, there must be a neighborhood centered at zA not containing a point from B. Since zA is a boundary point for A, there are points in every neighborhood that are not in A. Thus, in some neighborhood, there is a point z not in A and not in B. Hence, z ∉ E. By its construction then, we have that
zA < z,
and since z is in a neighborhood centered at zA, we also have that z < y since y ∈ B. Furthermore, remember that x < zA since x ∈ A. This gives us that
x < z < y,
meaning we’ve proved the conclusion of our contrapositve when zA ∈ A.
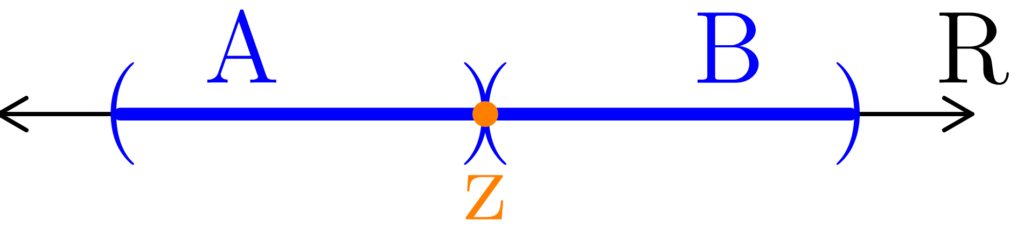
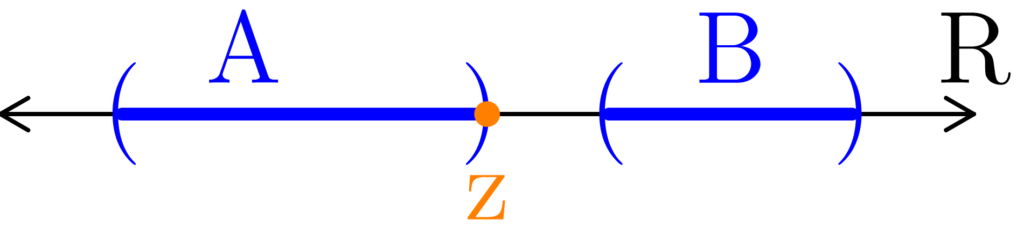
Figure 8: This is the situation where zA ∉ A. Notice that because A ∩ B = ∅, we have that zA ∉ B as well (remember that we still have zA ∈ A.) Whether separated by a single point (as in (a)), or an interval(as in (b)), we can always let z = zA. This gives us a point such that x < z < y and z ∉ E.
When zA ∉ A, then we can just let z = zA. Following the same logic as in the previous 4 paragraphs, we again have that
z ∉ E and x < z < y.
Thus the contrapositive is proven in all cases. And since we’ve just proven the contrapositive, we proved the original statement.
Now that we’ve proven both directions of the double implication, the entire proof is complete.