Closure of a Set

From the introductory section of this chapter, we’ve seen how inclusion or exclusion of an interval’s boundary points can affect whether or not a function achieves a maximum or minimum value over that interval. Even if the interval we’re working with is not closed, we may still want to examine a function’s behavior over that interval, including at its limit points.

Defining Closure

Closure

Let X be a metric space with E ⊆ X, and let E’ ⊆ X where E’ is the set of all limit points for E.

The closure of E is defined as the set E = E ∪ E’.

In essence, the closure of a set E is just the set E itself along with all of its limit points. Our focus will be on subsets of ℝ.

Figure 1: When dealing with subsets of ℝ, the closure of a set is basically just the set itself including the boundary points. In (a), we see the set E. In (b), we see the set E’ of all limit points of E. Notice that all of the interior points of E are also limit points of E. In (c), we see the result of taking the union of E and E’.

Beyond just simple intervals, we can also take the closure of a combination of intervals.

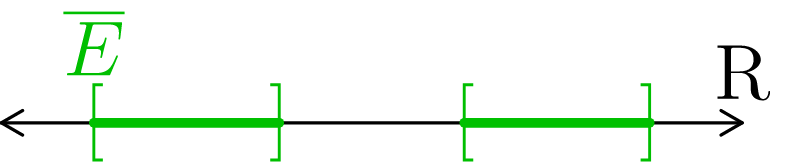
Figure 2: As in Figure 1, (a) represents the base set E. (b) represents the limit points of the set in (a). (c) is the union of the sets from (a) and (b).

Properties of the Closure

Since the closure of a set contains all the limit points of the underlying set, we’re tempted to conclude that the closure of a set is itself closed. Is this true though? Suppose E is the underlying set, and that E is the closure of E. How do we know that E does not have its own limit points independently of E? We will prove this in a general metric space.

Theorem 1

Let X be a metric space with E ⊆ X. Then E is closed.

Proof

General Strategy: Here, we’ll appeal to the topological definition of closed set. We’ll show that the complement of E within X is open. We do this by showing that every point in (E)^C is an interior point of (E)^C. This means that for any arbitrary point in (E)^C, we will show that it has a neighborhood without any points of E, and without any limit points of E.

Let p ∈ (E)^C. Because E = E ∪ E’, we have by DeMorgan’s Laws that

(E)^C = (E ∪ E’)^C = E^C ∩ (E’)^C ⊆ (E’)^C.

Therefore, because p ∈ (E)^C and (E)^C ⊆ (E’)^C, we have that

p ∈ (E’)^C.

This means that p is not a limit point for E.

Because p is not a limit point for E, there must exist some r > 0 such that

N_r(p) ∩ E = ∅.

So N_r(p) does not contain any points from E. We still need to show that N_r(p) does not contain any limit points of E.

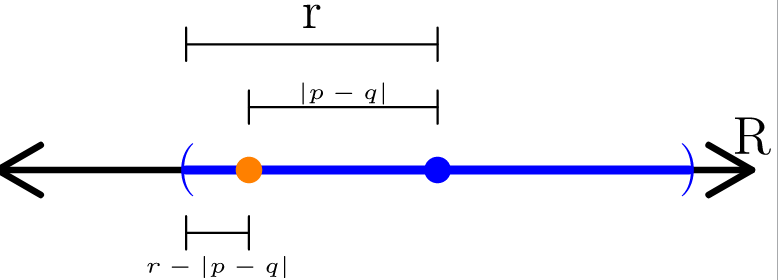
Figure 3: Here, we show why a limit point of E can’t be within a neighborhood of p ∈ (E)^C. In (a) we start with the neighborhood centered at p. In (b), we identify the point q with N_r(p). In (c), we figure out the largest radius we can give a neighborhood centered at q to be entirely contained within N_r(p). Here, we color the neighborhood centered at p blue, and the neighborhood centered at q orange. In (d), we see that the orange neighborhood is contained entirely within the blue neighborhood as desired. Finally, in (e), we identify a point e within the orange neighborhood that is in E. If this were to happen, then N_r(p) couldn’t be a subset of (E)^C. This is a contradiction.

Presume – for the purpose of showing a contradiction – that q is a limit point of E, and that q ∈ N_r(p).

Because q ∈ N_r(p), the neighborhood with radius r – |p – q| centered at q is entirely contained within N_r(p); symbolically, we have that

N_{r-|p – q|}(q) ⊆ N_r(p).

However, since q is a limit point for E, that means that N_{r-|p – q|}(q) contains a point from E, and since we have that N_{r-|p – q|}(q) ⊆ N_r(p), we must have that N_r(p) contains a point from E.

This contradicts the fact that N_r(p) ∩ E = ∅. Thus, if q is a limit point for E, it can’t be within N_r(p).

At this point, we now know that N_r(p) does not contain any points from E, nor does it have any limit points of E, and so we must have that

N_r(p) ⊆ (E)^C,

making p an interior point of (E)^C.

Since p was arbitrarily chosen within (E)^C, every point in (E)^C is an interior point of (E)^C.

Thus, by the topological definition of closed set, since (E)^C is open, we have that E is closed as desired.

Now that we know that E is closed, the next result is somewhat straight-forward.

Theorem 2

E = E ⇔ E is closed.

Proof

General Strategy: In either direction, we essentially just appeal to the definitions of the entities involved.

E = E ⇒ E is closed

Suppose that E = E.

Because E = E ∪ E’, we have that

E’ ⊆ E.

Since E = E, this means that E’ ⊆ E. Thus E contains all of it’s limit points.

This means that E is closed as desired.

E = E ⇐ E is closed

Suppose E is closed.

Then by definition, E contains all of it’s limit points. Symbolically, we say that

E’ ⊆ E.

Therefore, we have that

E = E ∪ E’ = E.

Therefore, we have that E = E as desired.

What happens when a closed set F ⊆ X contains E as a subset? Since F is closed, we would probably suspect that F contains all of E’s limit points as well. Wouldn’t this mean that E ⊆ F?

Theorem 3

Suppose F ⊆ X is a closed set with E ⊆ F.

E ⊆ F.

Proof

General Strategy: This is almost true by definition of closed set. Here, we show that if p is a point in E, then it must be a point in F as well.We basically just need to show that p ∈ E ⇒ p ∈ F and that p ∈ E’ ⇒ p ∈ F.

Suppose p ∈ E. Then p ∈ E ∪ E’.

If p ∈ E, then since E ⊆ F, we have that p ∈ F.

On the other hand, if p ∈ E’, then p is a limit point of E (by definition of E’.)

Since p is a limit point of E, that means that

∀r > 0 [N_r(p) ∩ E ≠ ∅] ⇒ ∀r > 0 [N_r(p) ∩ F ≠ ∅].

This means that p is also a limit point for F. Since F is closed, we have that p ∈ F.

In either case, whether p ∈ E or p ∈ E’, we have that p ∈ F.

Thus, we have that

E ∪ E’ ⊆ F ⇒ E ⊆ F

as desired.

Theorem 3 on this page gives us an interesting result. Of course, any closed set containing E will also contain E’ (as we just determined in Theorem 3.) But what is the “smallest” closed set containing E? Is there a closed set smaller than E satisfying this requirement?

Theorem 4

E is the smallest closed set containing E. In other words, if F is closed and F ⊂ E, then E ⊈ F.

Proof

General Strategy: Here, we show that taking E ⊆ F yields a contradiction. By taking E ⊆ F, we assume that every point in E is a point of F. However, by saying F ⊂ E, we say that there are points in E that are not in F. Theorem 3 makes this impossible.

Suppose that F is closed and F ⊂ E.

Presume – for the purposes of showing a contradiction – that E ⊆ F.

Then, by Theorem 3 on this page, since F is closed and E ⊆ F, we must have that E ⊆ F.

This contradicts the fact that F ⊂ E. Hence, it must be the case that E ⊈ F as desired.