Closed Sets

As we were working with sets in the previous page, we either described a set as “open” or “not open.” In other words, once we determined that a set was not open, we did not refer to it as “closed.” The word “closed” has a specific meaning when referring to sets.

Nevertheless, the words “open” and “closed” are related to each other. As a matter of fact, the word “closed” is defined by referring to open sets. Throughout this page, we’ll develop an equivalent definition of a closed set.

The Topological Definition

The most general and flexible definition of a closed set is perhaps the topological definition. Here, we define a closed set using open sets.

Closed Set

Let X be a metric space.

A set E ⊆ X is a closed set if X \ E is an open set.

Basically, closed sets are defined as the complements of open sets. Once we know that a particular set is open, we know that it’s complement is closed. Of course this also works the other way: if we know that a set E is closed, then the set X \ E is open.

Based on this definition, we already have several examples of closed sets.

(a, b) is open	⇔	(-∞, a] ∪ [b, ∞) is closed
(-∞, a) is open	⇔	[a, ∞) is closed
(b, ∞) is open	⇔	(-∞, b] is closed

∅ and ℝ

Since ℝ is the metric space being examined here, we notice that because

ℝ \ ℝ = ∅
ℝ \ ∅ = ℝ

we have that

ℝ is closed
∅ is closed

As a matter of fact, ∅ and ℝ are the only subsets of ℝ that are both open and closed. Sometimes, sets that are both open and closed are referred to as “clopen.”

Limit Points

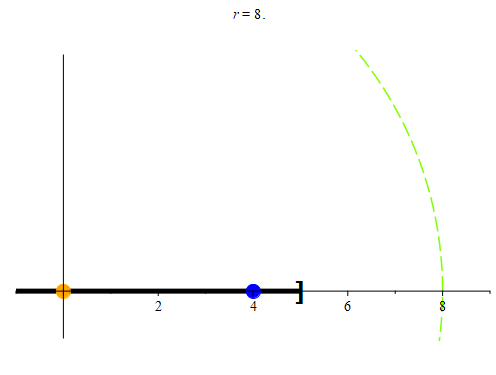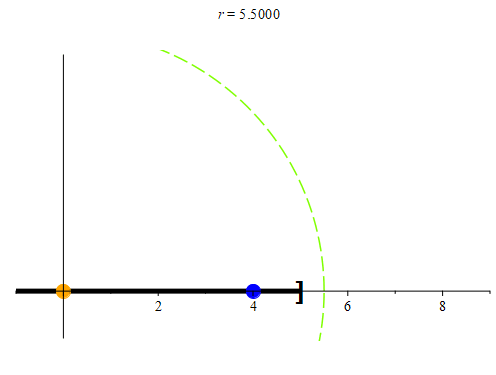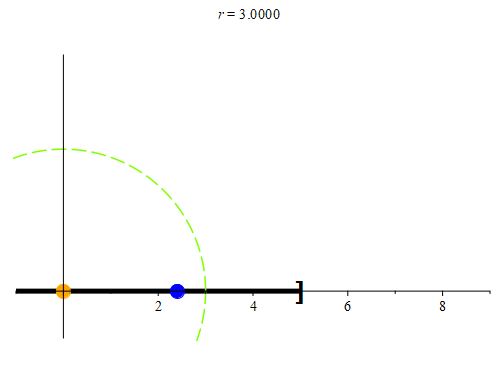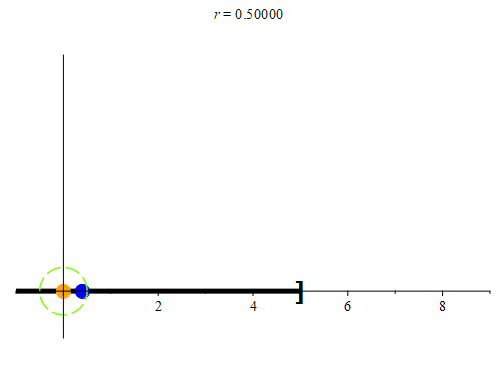
Figure 3: When examining the point 0, no matter how small we make its neighborhood, we can always find a point (colored blue here) that is in both the neighborhood N_r(0) and in (-5, 5]. When the radius r is bigger than 5, we have that

4 ∈ N_r(0) ∩ (-5, 5].

When the radius r is less than 5, we have that

0.8 * r ∈ N_r(0) ∩ (-5, 5].

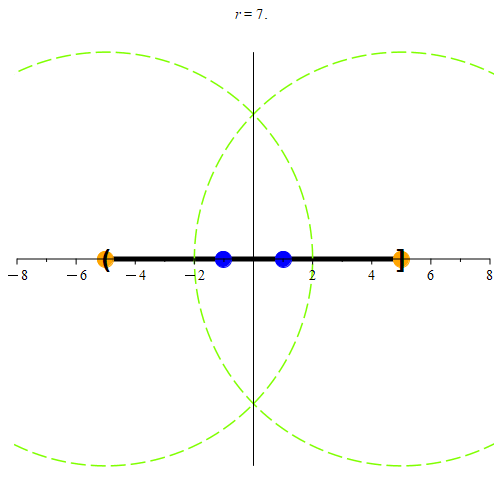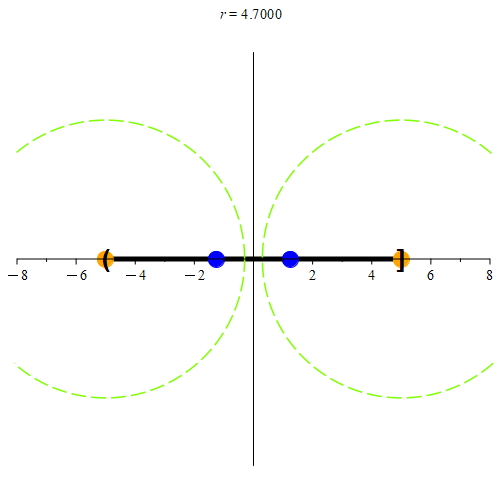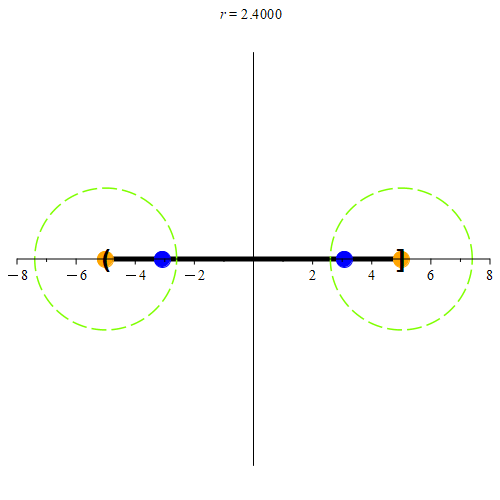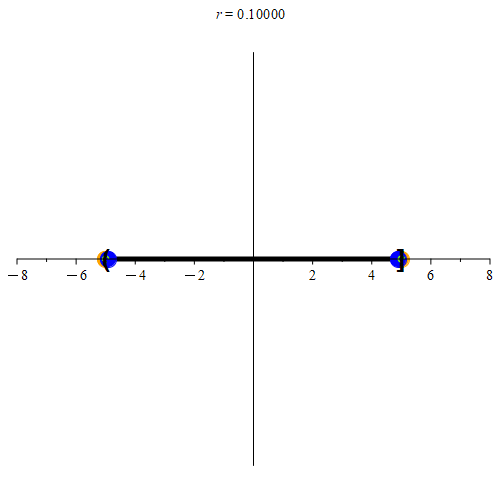
Figure 4: Continuing from Figure 3, we examine the endpoints next. Every neighborhood centered at -5, or at 5 will always have a point that is also in (-5, 5]. Again, we color some example points in blue.

The current definition we have for an open set can be a bit cumbersome. In order to determine if a set is open, we have to look at the set’s complement, not the set itself. It’s an extrinsic definition. We’d like to be able to examine the set itself to determine if it’s closed or not: we’re looking for something more intrinsic.

When we defined open sets, we defined them based on whether every point in that set is an interior point of that set. Let’s take another look at some of the sets we’ve already determined were closed:

(-∞, a] ∪ [b, ∞)
[a, ∞)
(-∞, b]

Notice that all of these sets include their boundary points, and that these boundary points are not interior points. Interior points are defined in terms of neighborhoods, so perhaps we can examine the neighborhoods of the points of these sets to see if we can spot some special behavior.

Let’s take another look at the set (-5, 5]. We’ll consider neighborhoods centered at the points -8, -5, 0, 5, and 8. What happens when these neighborhoods have large radii?

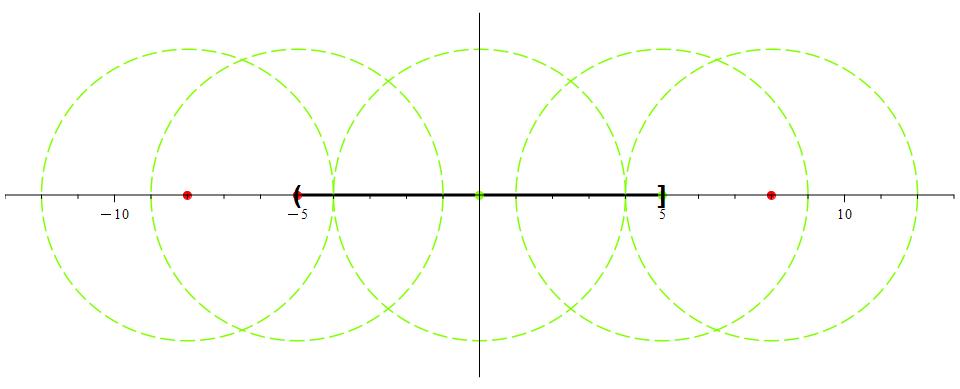
**Figure 1:** Pictured here are the points -8, -5, and 8 which are colored red because they are not in (-5, 5]. We also have points 0 and 5 which are colored green because they are in (-5, 5]. Centered at each point is a neighborhood of radius 4. Each neighborhood is colored green because each neighborhood contains points within(-5, 5]. Notice that each neighborhood contains points distinct from the point at which it’s centered.

If we put a neighborhood of radius 4 around each point, then each neighborhood will contain a point in (-5, 5]. By definition, the point at which a neighborhood is centered will be in the neighborhood, so we disregard that point when looking for points contained in both the neighborhood and the interval. Here are some examples.

-4.5 ∈ N₄(-8) \ {-8} and -4.5 ∈ (-5, 5]
-3 ∈ N₄(-5) \ {-5} and -3 ∈ (-5, 5]
1 ∈ N₄(0) \ {0} and 1 ∈ (-5, 5]
3 ∈ N₄(5) \ {5} and 3 ∈ (-5, 5]
4.5 ∈ N₄(5) \ {-5} and 4.5 ∈ (-5, 5]

When we make the radius ever smaller, eventually, some of the neighborhoods will no longer intersect (-5, 5].

**Figure 2:** From Figure 1, we reduce the radius of each neighborhood to 2. Notice that while the neighborhoods centered at -5, 0, and 5 still intersect (-5, 5], the neighborhoods of -8 and 8 no longer intersect (-5, 5].

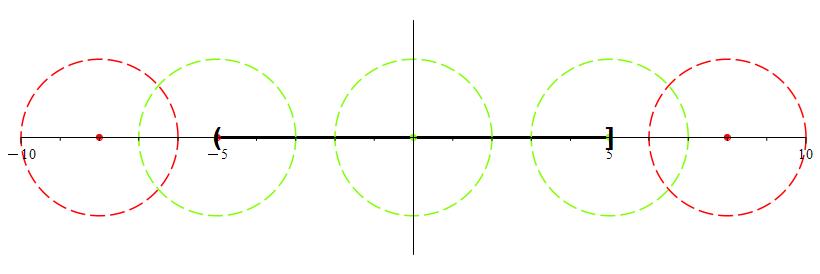
As illustrated in Figure 2, the neighborhoods of radius 2 centered at -8 and 8 do not share a point with (-5, 5]. The neighborhoods of radius 2 centered at -5, 0, 5 still do however.

The distinguishing feature between all of these points is the fact that for some of the points, every neighborhood will intersect (-5, 5]. For other points, we can find a neighborhood that does not intersect (-5, 5]. With this in mind, we have the following definition.

Limit Point

Let X be a metric space with E ⊆ X.

Let p ∈ X. If (N_r(p) \ {p}) ∩ E ≠ ∅ for all r > 0, then p is a limit point of E. In other words, if every neighborhood of p intersects E at some point other than p itself, then p is a limit point of E.

Notice that in the definition for limit point, we need p to be a point of the embedding metric space, but we don’t necessarily need p to a be a point of the set we’re examining. For example, notice that while -5 ∉ (-5, 5], every neighborhood centered at -5 still intersects (-5, 5] at some point other than -5. Hence, -5 is a limit point of the set (-5, 5].

Based on this definition, we see that every point in [-5, 5] is a limit point of (-5, 5] as well. Any point not in [-5, 5] will not be a limit point of (-5, 5] as demonstrated in Figure 5.

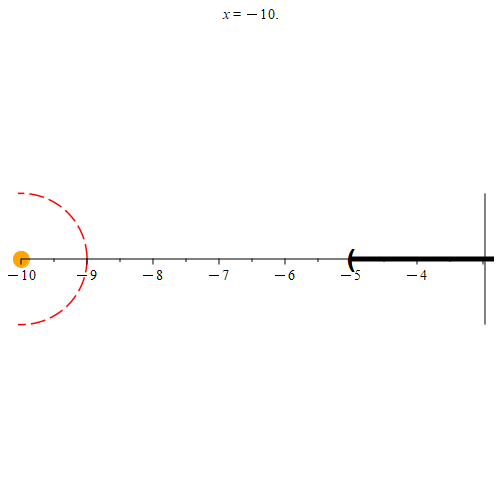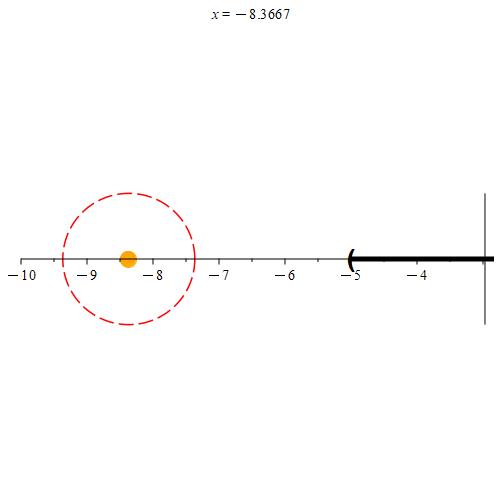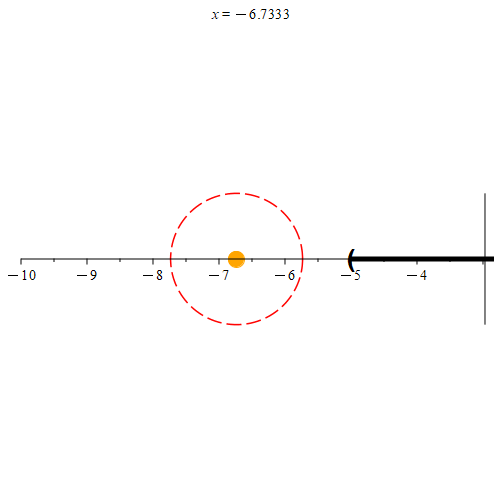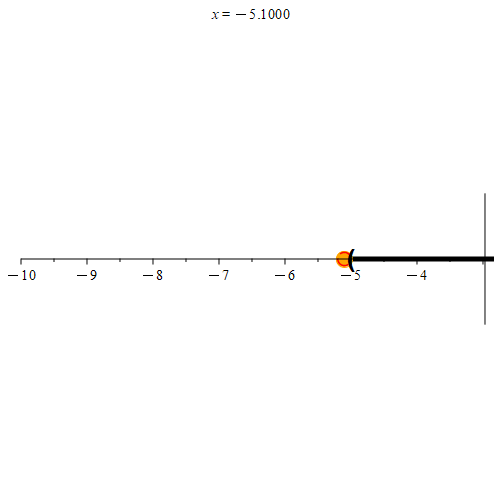
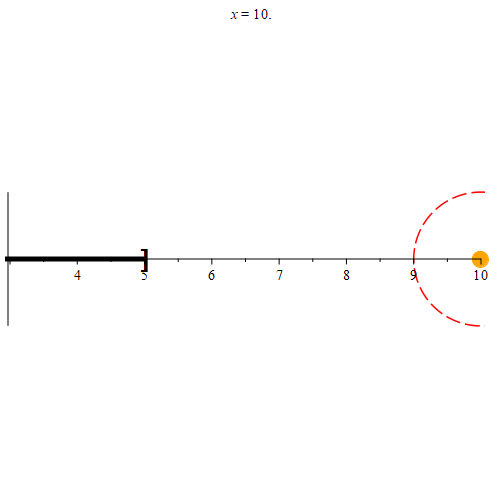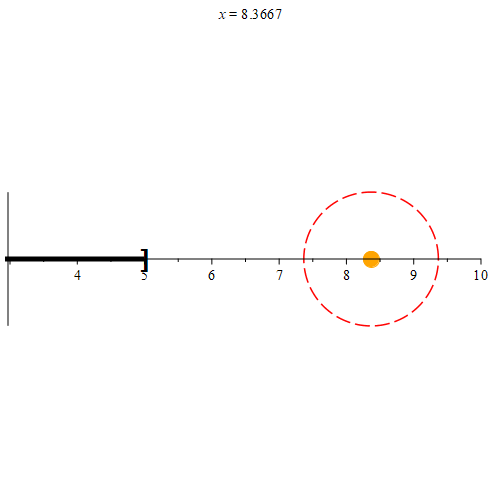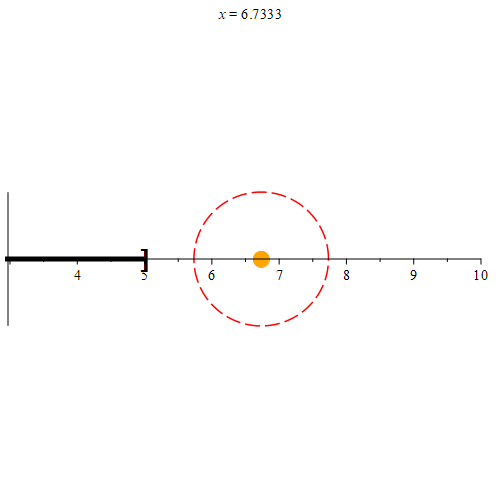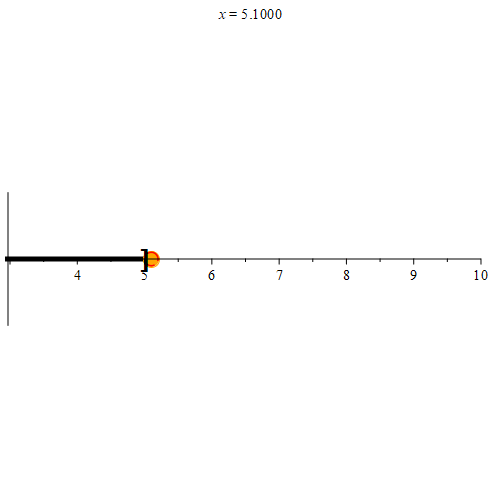
**Figure 5:** In the above animation, we track a series of points that are less than -5, and a series of points that are greater than 5. For any points less than -6 or greater than 6, a neighborhood of radius 1 will not intersect (-5, 5]. For any point x closer than 1 to -5, a neighborhood of radius -5 – x will not intersect (-5, 5], so x will not be a limit point for (-5, 5]. Similarly, for any point x greater than 5, the neighborhood of radius x – 5 will not intersect (-5, 5], so it won’t be a limit point of (-5, 5]. In summary, none of the orange points displayed above are limit points of (-5, 5].

Closed Sets via Limit Points

How are interior points and limit points related? Suppose that the point p is an interior point of set E. Since p is an interior point of E, some neighborhood N_r(p) must be a subset of E. Every subset of N_r(p) must also be a subset of E. Since a neighborhood will have a radius larger than 0, these neighborhoods all have points that are distinct from p. Thus, every neighborhood of p will contain some point q ≠ p that is also in E. Hence p must also be a limit point of E.

Notice that since we selected p arbitrarily, we must have that every interior point is a limit point. However, as demonstrated by our example interval (-5, 5], even though 5 is a limit point of (-5, 5], it is not an interior point of (-5, 5]. We thus have the following:

p is an interior point of E ⇒ p is a limit point of E
p is a limit point of E ⇏ p is an interior point of E

Think back to our first example of an open set (a, b). Based on the topological definition of closed set, we know that

(-∞, a] ∪ [b, ∞)

is a closed set. The set of interior points of this set is (-∞, a) ∪ (b, ∞), which is a subset of (-∞, a] ∪ [b, ∞). Based on the previous two paragraphs, we know that all of the points in (-∞, a) ∪ (b, ∞) are also limit points of (-∞, a] ∪ [b, ∞).

Furthermore, we notice that the points a and b are limit points, but are not interior points of (-∞, a] ∪ [b, ∞). Nevertheless, we still have that a ∈ (-∞, a] ∪ [b, ∞) and b ∈ (-∞, a] ∪ [b, ∞).

There are no other limit points of (-∞, a] ∪ [b, ∞), so the set (-∞, a] ∪ [b, ∞) contains all of its limit points. Do all closed sets contain all of their limit points?

Theorem:

Suppose X is a metric space with E ⊆ X.

E is closed ⇔ E contains all of its limit points.

Proof

E is closed ⇒ E contains all of its limit points

General Strategy: Pick an arbitrary limit point p of E, and show that p ∈ E. We can do this by showing that
p ∉ X \ E.

Let p be an arbitrarily chosen limit point of E. Then by definition of limit point, every neighborhood of p intersects E at some point other than p itself. Symbolically, we would say that

∀ r > 0 [ N_r(p) \ {p} ∩ E ≠ ∅ ].

We will denote this point as p’. Symbolically, we could write

	p’ ∈ N_r(p) \ {p} ∩ E
⇒	p’ ∈ E
⇒	p’ ∉ X \ E

Because E is closed, we know that X \ E must be open. By definition of an open set, every point of X \ E must be an interior point of X \ E.

However, notice that because every neighborhood of p has some point p’ ∉ X \ E, no neighborhood of p can be a subset of X \ E. Symbolically, we write

∀ r > 0 [ N_r(p) \ {p} ⊈ X \ E ]

Thus, p is not an interior point of X \ E, and since every point of X \ E is an interior point of X \ E, we must have that

p ∉ X \ E.

This means that p ∈ E. Note that since p was an arbitrarily chosen limit point of E, this means that E must contain all of its limit points. This completes the ⇒ direction.

E is closed ⇐ E contains all of its limit points

General Strategy: We show that X \ E must be open. We do this by picking an arbitrary point in X \ E, and show that it must be an interior point of X \ E.

Start by picking an arbitrary point q of X \ E.

Because q ∈ X \ E, we must have that q ∉ E. Because E contains all of it’s limit points, this means that q is not a limit point of E.

Because q is not a limit point of E, there must exist some r > 0 such that

N_r(q) \ {q} ∩ E = ∅

Therefore, no point of N_r(q) is in E, and thus we must have N_r(q) ⊆ X \ E. This means that q is an interior point of X \ E.

Because q was an arbitrarily picked point of X \ E, we have that every point of X \ E is an interior point. Thus by definition, X \ E is open.

Finally, because X \ E is open, we have that E must be closed as desired. This completes the ⇐ direction.

This theorem thus gives us a new, equivalent definition of closed set.

Closed Set (via Limit Points)

Let X be a metric space with E ⊆ X.

E is a closed set if it contains all of its limit points.

The Interval [a, b]

Using this new definition for closed sets, we can deduce that

[a, b]

is also a closed set for any real numbers a and b where a ≤ b. Technically, we weren’t able to figure this out from the topological definition – at least not using the examples we already knew about. Perhaps this isn’t too surprising.

We could have appealed to the topological definition to figure this out (instead of just our intuitions) if we knew that

(-∞, a) ∪ (b, ∞)

was an open set. A close examination will reveal that all of its points are interior points, but will a union of open sets always yield another open set? What about an intersection of two open sets? What if we took a union of an arbitrarily large number of open sets? We could ask the same thing about closed sets as well.

In the next section, we’ll examine what happens when we combine open sets via unions and intersections, and we’ll do the same thing for closed sets as well.