Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Probabilities of 0 and 1
Based on our current theory, for an experiment with sample space S, we have that
p(∅) = 0, p(S) = 1.
Furthermore, for some event E ⊆ S, we have that
0 ≤ p(E) ≤ 1.
Notice that the inequalities are inclusive: p(E) may be equal to 0, or it may be equal to 1. This is certainly the case when E = ∅ or when E = S respectively. This does not always need to be the case. There are events – not equal to ∅ or S – that have probabilities of 0 and 1. In this section, we explore one such example.
Picking a Single Point from an Interval
Consider an experiment where a single point is chosen randomly from the interval [0, 1]. The sample space S of this experiment consists of all real numbers between 0 and 1 inclusive. Each of these numbers has a decimal representation of the form
0.α1α2α3α4α5…αn-1αnαn+1…
where each αi is one of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9.
Some numbers, such as e – 2, have infinitely many non-repeating decimal expansions as in
0.718 281 828 459 ….
Some other numbers have infinitely repeating decimal expansions like the number 1 ÷ 7, which has decimal expansion
0.142 857 142 857 142 857 ….
Still other numbers actually have finitely many non-zero digits after the decimal, like 1 ÷ 4 which has decimal representation
0.25.
For any number with only a finite number of non-zero digits past the decimal point, we are going to append an infinite number of zeros after the last non-zero digit, so a number like 1 ÷ 4 would have decimal representation
0.250 000 000 000 000 ….
Modeling the Selection Process
Suppose we wanted to calculate the probability of randomly selecting the number
0.111 111 111 111 111 111 …
where every digit past the decimal is 1.
We can model this problem as a sequence of stages:
| Stage 1: | Pick the first digit correctly |
| Stage 2: | Pick the first two digits correctly |
| Stage 3: | Pick the first three digits correctly |
and so on.
Consider the first stage. Here we just want to pick the digit 1. This means that there is only 1 possible outcome we want to occur. There are a total of 10 choices (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). So, the probability of selecting the correct digit is 
.
For the second stage, we are now picking a sequence of two digits. There are 100 two-digit sequences (00, 01, 02, 03, …, 96, 97, 98, 99). Only one of these sequences is the sequence we want (11). Thus, the probability of successfully choosing the first two digits is 
For the third stage, we have to successfully pick three digits. There are 1000 three-digit sequences (000, 001, 002, 003, …, 996, 997, 998, 999). Only one of these sequences is the sequence we want (111). Thus, the probability of successfully choosing the first three digits is 
.
We can summarize this model using a table of values.
| Stage | Desired Selection | Number of Possible Choices | Probability of Choosing Correct Digit Sequence |
|---|---|---|---|
| 1 | 1 | 10 | |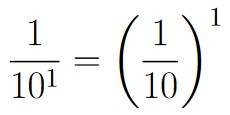
| 2 | 11 | 100 | |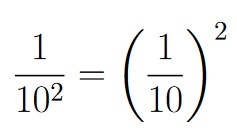
| 3 | 111 | 1000 | |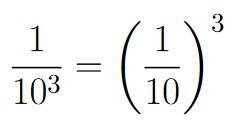
| 4 | 1111 | 10000 |  |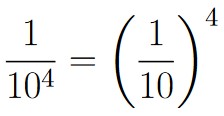
| … | |||
| n-1 | 111…1… | 10n-1 |  |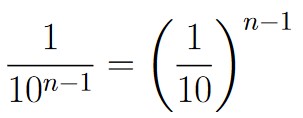
| n | 111…11… | 10n |  |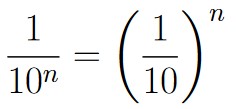
| n + 1 | 111…111… | 10n+1 |  |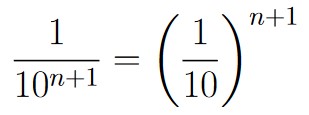
| … |
Calculating the Probability
Notice that the way we modeled our selection process allows us to define the following events:
| E1: | The first digit is 1 |
| E2: | The first two digits are 11 |
| E3: | The first three digits are 111 |
| E4: | The first four digits are 1111 |
| … | |
| En: | The first n digits are 1111…1 |
| … |
Each event is a subset of subsequent events because the occurrence of event En depends on the occurrence of event En-1:
E1 ⊆ E2 ⊆ E3 ⊆ E4 ⊆ … ⊆ En ⊆ ….
As such, we can invoke Theorem 1.7.1 to calculate E∞ which represents the limiting union event where every digit in the infinite sequence of digits chosen is a 1:
Interpreting the Result
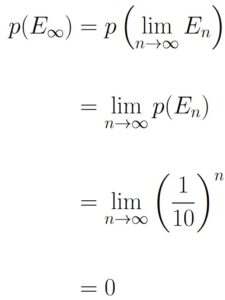
Based on the calculation, we would conclude that the probability of choosing a number from the interval [0, 1] with decimal expansion
0.111 111 111 111 111 …
is 0. This means that this event is mathematically impossible. No matter how many times we pick a random point from the interval, we will never pick the desired number.
Now we can consider the complementary event. What’s the probability that the number we randomly choose is not
0.111 111 111 111 111 …?
Any real number from the interval [0, 1] will satisfy the requirement as long as it’s not just an infinite sequence of 1s. We would calculate the probability as simply
1 – 0 = 1.
That is to say, it is guaranteed that any number we pick will satisfy the requirement that not all digits after the decimal are 1s.