Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Continuity of the Probability Function
Some hypothetical experiments we wish to analyze involve repeating some procedure ad infinitum. For example, one such experiment may involve randomly picking digits from 0 to 9 in order to form a real number in the interval [0, 1]. We may wonder what the probability is for generating the number π – 3. In this case we would define En as the event corresponding to picking the first n digits. For this problem, we would have that
E1 = 1
E2 = 14
E3 = 141
E4 = 1415
E5 = 14159
…
For this experiment, what we essentially want to do is to form the number 0.E∞. We would need to know the limiting behavior:
Special Event Sequences
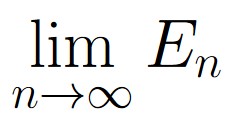
Notice that when we introduced the idea of picking the first n digits of π – 3, the events we defined form a sequence of digits. We essentially defined our events in a way that any event “captures” all previous events:
E1 ⊆ E2 ⊆ E3 ⊆ E4 ⊆ E5 ⊆ …
The fact that we form a subset chain will prove useful later, so we capture the idea now.
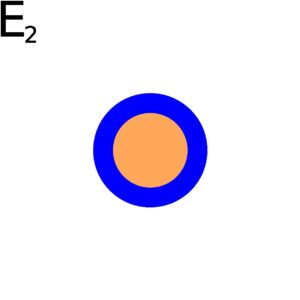
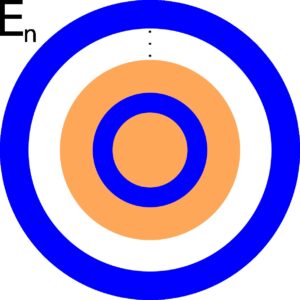
Figure 1.7.2: In (a), we start with the first set in the increasing sequence. In (b), we see that event E1 is a subset of E2. We can keep this procedure of incorporating earlier sets into later sets, as seen in (c). In (c), we show that the nth event contains all previous events as subsets (represented by the ellipses.)
Increasing Sequence of Events
A sequence of events
from a sample space is called an increasing sequence of events if
Em ⊆ En
for any m ≤ n; in other words, if
E1 ⊆ E2 ⊆ E3 ⊆ … En ⊆ En+1 ⊆ …
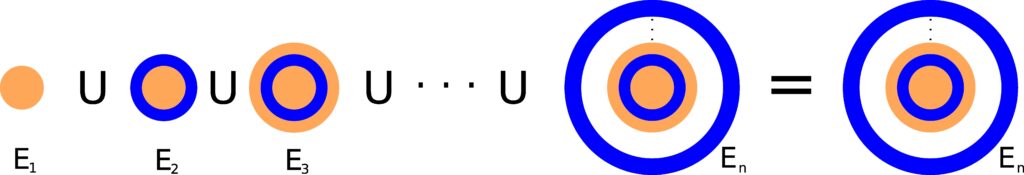
Figure 1.7.1: Based on how En was defined, taking a union of all Ei from i = 1 to i = n yields En.
Because we have that
Em ⊆ En, m ≤ n
every Em is just a subset of En, and so taking a union of all Em from m = 1 to m = n will give us the nth set in the sequence. The fact that each set is a union of all previous sets is going to allow us to invoke Axiom 3 and Theorem 1.4.2.
Limiting Union Event
For a given increasing sequence of events
we say the event E∞ is the event that at least one Ei, 1 ≤ i occurs. In other words,
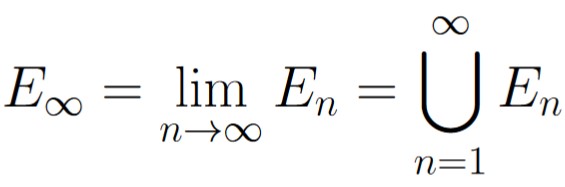
which we’ll refer to as the limiting union event for the given increasing sequence of events.
We can do the define the same things if the events are increasingly contained within previous events.
Decreasing Sequence of Events
A sequence of events
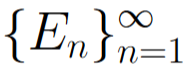
from a sample space is called a decreasing sequence of events if
Em ⊇ En
for any m ≤ n; in other words, if
E1 ⊇ E2 ⊇ E3 ⊇ … En ⊇ En+1 ⊇ …
Limiting Intersection Event
For a given increasing sequence of events
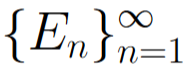
we say the event E∞ is the event that at every Ei, 1 ≤ i occurs. In other words,
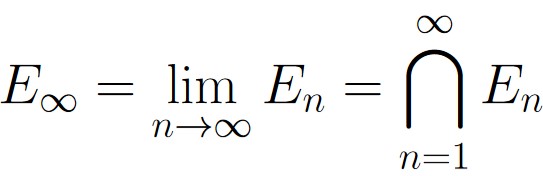
which we’ll refer to as the limiting intersection event for the given decreasing sequence of events.
With this, we’re ready to start looking at probabilities associated with these kinds of events.
Probabilities of Limiting Events
We first examine the limiting union event for an increasing sequence of events.
Theorem 1.7.1
For an increasing sequence of events ,
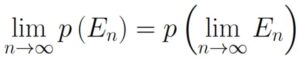
General Strategy: We define a new sequence of mutually exclusive events using the given increasing sequence of events. Once we equate the two, we can use Axiom 3 and Theorem 1.4.2.
We start by defining a new sequence of events 
as follows:
F1 = E1,
Fn = En – En-1
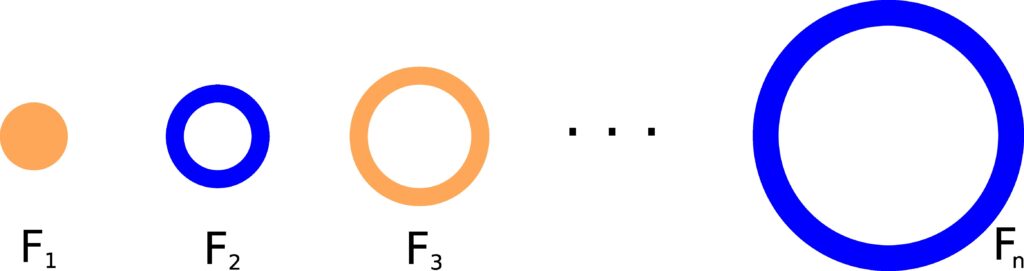
Figure 1.7.3: As defined, all Fn are mutually exclusive to each other.
Based on our definition, each Fn is just the part of En that does not include any part of En-1. Based on how each En is defined, this basically means that each Fn doesn’t contain any part of E1, E2, …, En-1. This means that each Fn is mutually exclusive to each other.
Notice that by taking a union of all Fi from i = 1 to i = n, we are going to form En:
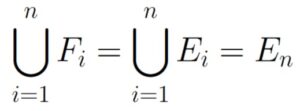
This will be true for all n ∈ ℕ:
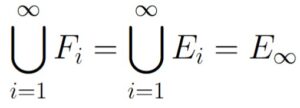
With this equivalence, we’ll be able to invoke Theorem 1.4.2:
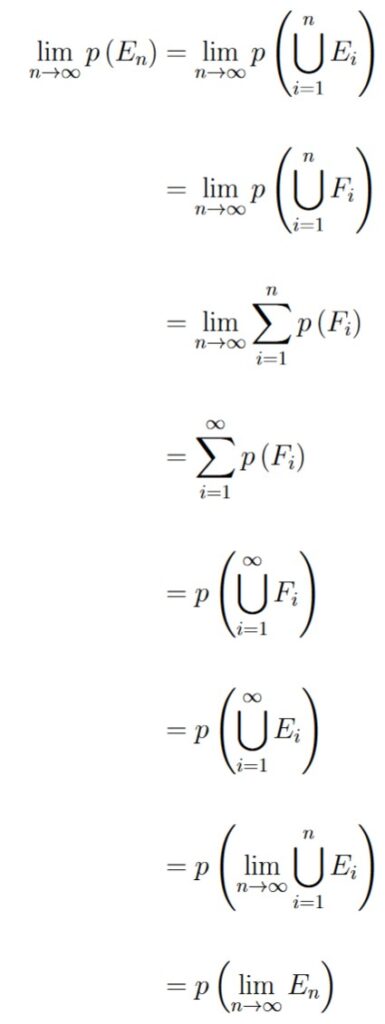
This gives us the desired result, and completes the proof.
Based on this result, we can derive a similar result for decreasing sequences.
Theorem 1.7.2
For a decreasing sequence of events ,
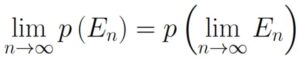
General Strategy: We start by taking the complement of the decreasing sequence of events. The complement of a decreasing sequence of events will be an increasing sequence of events. We invoke Theorem 1.7.1to finish the proof.
We start by substituting in definitions of previously defined terms:
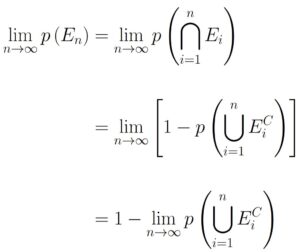
Now, notice that because we have a decreasing sequence of events, the complement will be an increasing sequence of events. In other words,
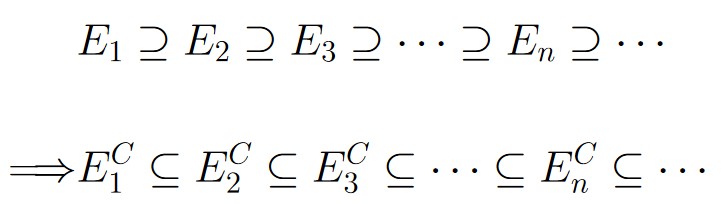
Now we can invoke Theorem 1.7.1:
This is the desired result.
An Experiment with a Limiting Intersection Event
Suppose we’re given an infinitely large urn. Consider an experiment where, one minute before midnight, balls labeled 1 through 10 are placed in the urn, and one of them is immediately picked out. Then, at half a minute before midnight, balls labeled 11-20 are placed in the urn, and now one of the remaining 19 balls is immediately drawn at random. Next, at a quarter of a minute before midnight, balls 21-30 are placed in the urn and one of the remaining 28 is immediately drawn at random, and so on indefinitely.
| Minutes Before Midnight | Balls Placed in the Urn | Number of Balls Before Draw | Number of Balls Immediately Drawn | Number of Balls Remaining After Draw |
|---|---|---|---|---|
| 1 | 1 – 10 | 10 | 1 | 9 |
| 0.5 | 11 – 20 | 19 | 1 | 18 |
| 0.25 | 21 – 30 | 28 | 1 | 27 |
| 0.125 | 31 – 40 | 37 | 1 | 36 |
| … | … | … | … |
Let’s focus our attention on the ball labeled 1. What’s the probability that, at exactly midnight, it is still in the urn? We’ll break this problem down into several steps.
1.) Defining the Events
Lets define the following events:
| E1 | = | The ball labeled 1 is still in the urn after the first draw |
| E2 | = | The ball labeled 1 is still in the urn after the first two draws |
| E3 | = | The ball labeled 1 is still in the urn after the first three draws |
| E4 | = | The ball labeled 1 is still in the urn after the first four draws |
| … | ||
| En | = | The ball labeled 1 is still in the urn after the first n draws |
| … |
To calculate the probability of each event, note that we essentially can select any of the remaining balls except for one of them. In this experiment, we can assume uniform randomness, which is to say that we assume all balls are equally likely to be drawn. This allows us to invoke Theorem 1.6.1 like so:
| p(E1) | = |  |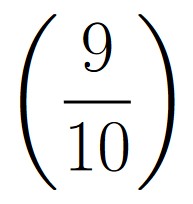
| p(E2) | = |  |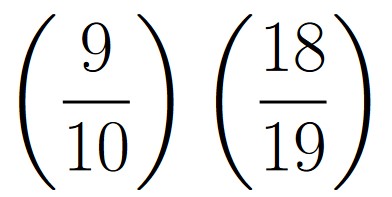
| p(E3) | = |  |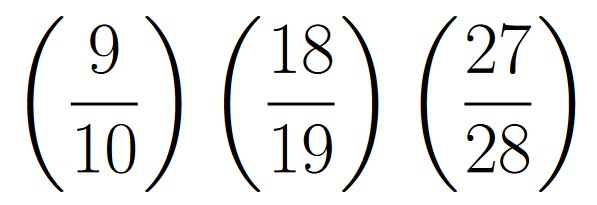
| p(E4) | = |  |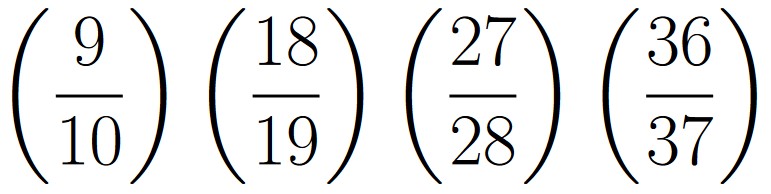
| … | ||
| p(En) | = |  |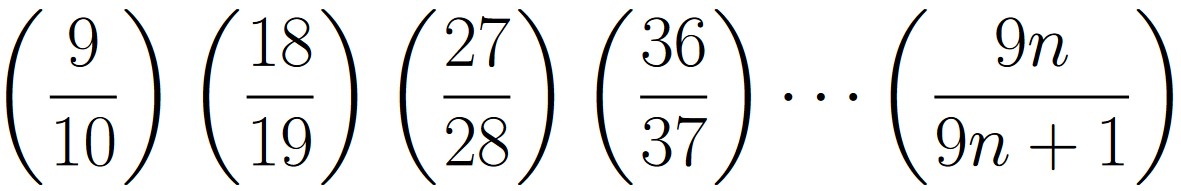
| … |
2.) Exploiting the Decreasing Sequence of Events
Based step 1, E∞ is the event where the ball labeled 1 is still in the urn at midnight. From here, we can use Theorem 1.7.2 by noticing that
E1 ⊇ E2 ⊇ E3 ⊇ … En ⊇ En+1 ⊇ …
because in order for event En to occur, every event E1 through En-1 must also occur. This gives us the following:
3.) Working with the Infinite Product
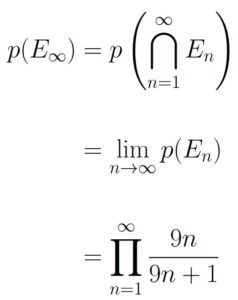
Because there is a sum in the denominator, it may be easier to work with the reciprocal. Start by noticing that
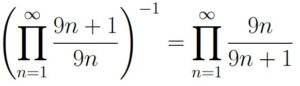
Next, we use the fact that for any integer m,
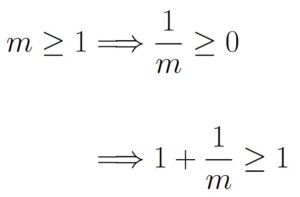
Now, using the previous two observations, we get the following for all integers m ≥ 1:
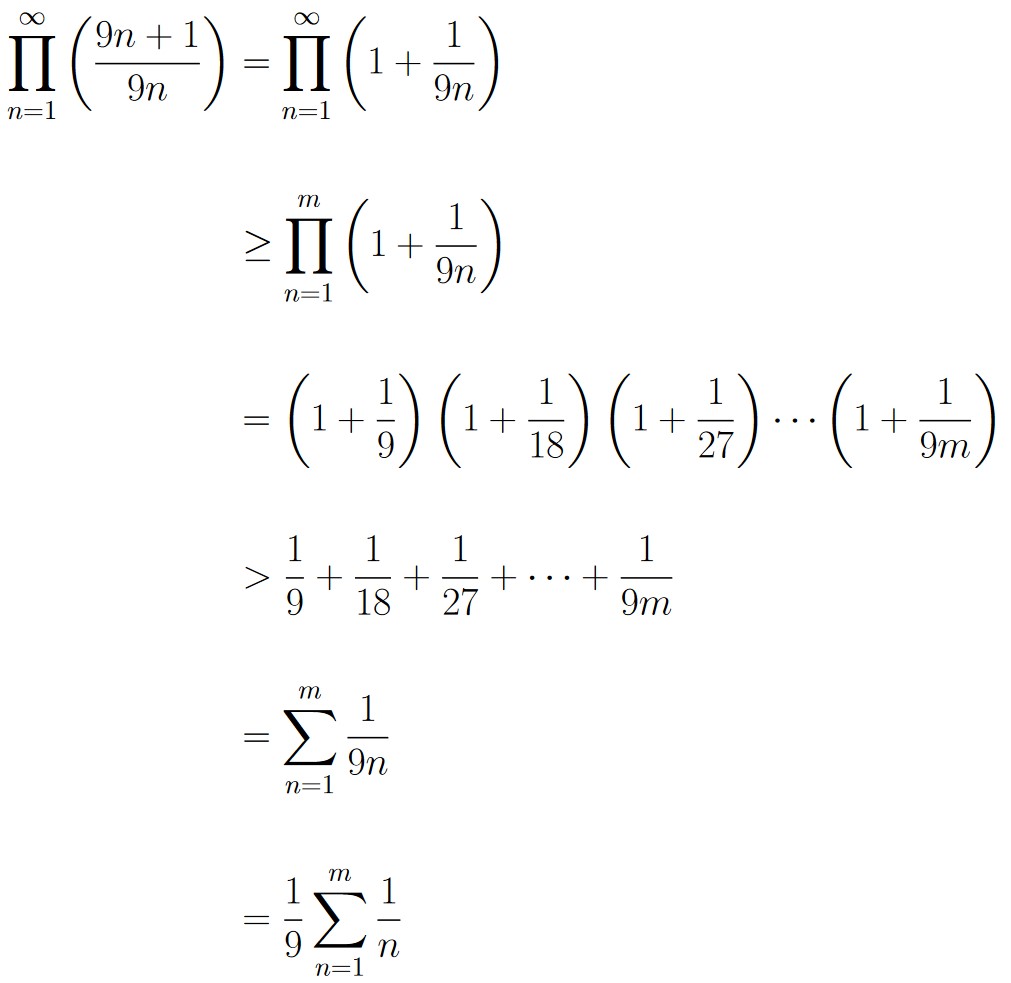
Notice that as m → ∞, the sum becomes the Harmonic Series, which diverges to ∞. As such, we must also have that
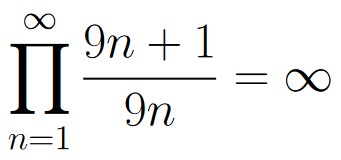
from which, we have that
4.) Concluding the Calculation
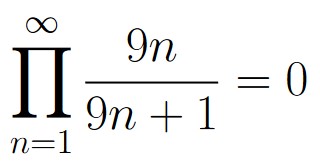
Notice that we just calculated the probability that the ball labeled 1 would still be in the urn at midnight. Apparently, the probability is 0, meaning it will definitely not be in the urn at midnight. Of course, there is nothing special about the ball labeled 1. The same analysis could be performed for any label.
Of course with balls labeled 11-20, the product would have to start with n = 2 since none of those labels are present upon the first drawing.