Physical Address

304 North Cardinal St.
Dorchester Center, MA 02124

The Book of
Foundational Mathematics

Detailed Contents

Propositional Logic
  1. Propositions
  2. Modeling Logic with Truth Tables
  3. Logical Equivalence
  4. The Laws of Logic
  5. Application: Switching Networks
  6. Logical Implications
  7. Propositions with Variables
  8. Quantifiers
  9. Logic with Quantified Statements
  10. Nested Quantifiers
  11. Application: Logic Puzzles
  12. A Primer on Fuzzy Logic
  1. Mathematical Logic with Maple
  2. Defining Propositions with Maple
Arguments and Proof
  1. The Structure of Basic Arguments
  2. Rules of Inference
  3. Using the Rules of Inference
  4. Logically Equivalent Arguments
  5. Invalid Arguments
  6. Universal Specification
  7. Universal Generalization
  8. Axioms, Definitions, Theorems, and Proofs
  9. Proof Technique: Direct Proofs
  10. Proof Technique: Indirect Proofs
  11. Proof Technique: Contradiction
  12. Mistakes in Proofs
  13. Proof Technique: Equivalence
  1. Verifying Mathematical Arguments in Maple
Set Theory
  1. Sets
  2. Subsets
  3. Proof Technique: Element Arguments
  4. A Set of Operations on Sets
  5. The Laws of Set Theory
  6. Proof Technique: Exhaustion
  1. Set Theory in Maple

The Structure of Basic Arguments

The heart of mathematics is not mere computation, but is instead the act of taking a combination of known facts, and combining those facts in some way to arrive at new conclusions. Think back to when you learned about the Pythagorean Theorem or the Quadratic Formula. While it is certainly true that these tools help you compute things, like the hypotenuse of a right triangle, or the roots of a quadratic function respectively, those activities are computational. Without the Pythagorean Theorem or the Quadratic Formula, how would we go about computing those quantities? There may be other methods available, but those two tools in particular are extremely helpful.

But why do those tools even exist? The answer lies in taking what’s known about right triangles and quadratic expressions, and coming to the now famous conclusions. Of course, the act of doing mathematics (arriving at new conclusions based on previous knowledge) can lead to incredibly efficient ways of performing computation. However, we stress that the difference between math and computation is like this: mathematics is knowing that for all right triangles, where the legs have lengths a and b, and the hypotenuse has a length of c, we have that

a2 + b2 = c2;

computation is being able to figure out that a right triangle with leg lengths of 5 and 12 has a hypotenuse of length of 13 using the Pythagorean Theorem.

In order to know anything in math, we start with what is currently known, and extrapolate from our prior knowledge. In mathematics, we call this providing an argument, or a proof. In this section, we examine the basic structure of such an argument.

Premises and Conclusions

Let’s elaborate on the idea of using existing knowledge. We essentially take a collection of known facts together. The amalgamation of all these facts provides some new fact, or piece of knowledge:

IF
known fact #1
AND
known fact #2
AND
known fact #3
AND
.
.
.
AND
known fact #n
THEN
new fact

Notice that we combine several facts using the word “and.” The reason is that all the facts are supposed to come together in order to create the new fact. If any facts can be left out, then those facts are not needed. This is the same situation we had with the logical conjunction ∧ operator. When we used that operator, then every premise attached to it had to be true in order for the conjunction to be true.

Let’s rewrite the above representation of an argument using mathematical notation, where we use p1 to represent known fact #1 (a fact is just another term for a proposition), p2 for known fact #2, p3 for known fact #3, and so on including pn for known fact #n, and we’ll use the letter c to denote the proposition representing the new fact:

(p1 ∧ p2 ∧ p3 ∧ … ∧ pn) → c.

It is somewhat common to write

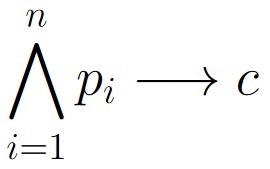
in place of something like

p1 ∧ p2 ∧ p3 ∧ … ∧ pn → c.

Figure 2.1.1: We can use a large “wedge” or “carat” symbol to represent repeated conjunction.

It is also somewhat common to write

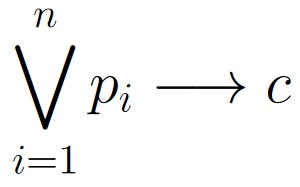
in place of something like

p1 ∨ p2 ∨ p3 ∨ … ∨ pn → c.

Figure 2.1.2: We can use as large “V” symbol to denote repeated disjunction.

The above expression, including the expression introduced in Figure 2.1.1 for the basic structure of an argument.

Argument, Premises, Conclusion

Consider a collection of some number n + 1 propositions

p1, p2, p3, …, pn, c.

An implication of the form

(p1 ∧ p2 ∧ p3 ∧ … ∧ pn) → c

is called an argument. The propositions p1, p2, p3, …, pn within the repeated conjunction are called premises of the argument. The proposition q is called the conclusion of the argument.

Notice that in the definition of argument, we do not require the premises to be primitive propositions. Each premise can be primitive. Each premise can be some long, complicated compound proposition. What matters is that we combine all premises into a conjunction.

Valid Arguments

Example 2.1.1

Let a, b, c represent the following propositions:

a:Dexter keeps his laboratory door locked.
b:Deedee sneaks into Dexter’s laboratory.
c:Dexter keeps his laboratory a secret from his parents.

Now consider an argument with the following premises:

p1:a → c
p2:¬b → a
p3:¬c

The argument we want to examine is

(p1 ∧ p2 ∧ p3) → b.

We know from Chapter 1, Section 1 that an implication is only false when the hypothesis is true (has a truth value of 1) and the conclusion is false (has a truth value of 0.) Looking at a truth table will help us analyze this argument:

p1p2p3p1 ∧ p2 ∧ p3(p1 ∧ p2 ∧ p3) → b
abca → c¬b → a¬c
0001010
0011000
0101111
0111100
100110
1011100
100110
1111100

Before we fill in the appropriate values for the last column, note that all of the 0 entries in the p1 ∧ p2 ∧ p3 column yield trivially true cases. We don’t care about those rows so much, because we’re only interested in what happens when all premises are true. Arguments rest on the truth of their premises. If even one premise is false, then the argument does not apply. We’ll just color those rows red for now.

p1p2p3p1 ∧ p2 ∧ p3(p1 ∧ p2 ∧ p3) → b
abca → c¬b → a¬c
0001010
0011000
0101111
0111100
1000110
1011100
1100110
1111100

Now, we finish the truth table by filling in the only one entry needed:

p1p2p3p1 ∧ p2 ∧ p3(p1 ∧ p2 ∧ p3) → b
abca → c¬b → a¬c
0001010
0011000
01011111
0111100
1000110
1011100
1100110
1111100

So, we see that every time the hypothesis (the conjunction of the premises p1, p2, p3) is true, then the conclusion is also true. Here is the entire table:

p1p2p3p1 ∧ p2 ∧ p3(p1 ∧ p2 ∧ p3) → b
abca → c¬b → a¬c
00010101
00110001
01011111
01111001
1001101
10111001
1001101
11111001

Because the last column consists entirely of 1s, we know that the implication

(p1 ∧ p2 ∧ p3) → b

is a tautology, and so we can write

(p1 ∧ p2 ∧ p3) ⟹ b.

Using Figure 2.1.1 as guidance, we could also write

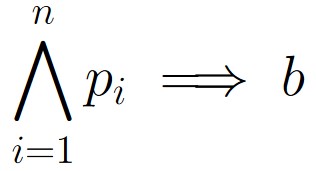
Thus, the argument is a logical implication. So, we conclude that if

“Dexter’s parents find out about his secret laboratory”,

“If Dexter keeps his laboratory door locked, the Dexter is able to keep his laboratory a secret from his parents”,

“If Deedee does not sneak into Dexter’s laboratory, then Dexter keeps his laboratory door locked.”

are all true propositions, then Deedee likely sneaked in to Dexter’s laboratory somehow.

Example 2.1.1 demonstrates something important about arguments: an argument asserts that, when all premises are true, then the conclusion is also true. If there are scenarios where all premises are true, but the conclusion is not true, then that particular argument does not accurately reflect when the conclusion is true.

In order for an argument to accurately reflect when the conclusion is true, then the conclusion must be true whenever the premises are true (otherwise, the argument is just wrong.)

On the other hand, we don’t care what happens when any of the premises are false. An argument is only supposed to tell us that if all premises are true, then so is the conclusion. Arguments do not apply when any of the premises are false because at that point, the argument is irrelevant.

Valid

Consider an argument of the form

(p1 ∧ p2 ∧ p3 ∧ … ∧ pn) → c.

If the implication is a tautology, meaning that it’s a logical implication with

(p1 ∧ p2 ∧ p3 ∧ … ∧ pn) ⟹ c,

then we call the argument a valid argument.

Mathematics is all about developing valid arguments, because these arguments form the base of knowledge we have. Arguments give us a way to come up with new and efficient ways to do calculations, make classifications, or make any other kinds of equivalencies.

Example 2.1.2

Consider the propositions denoted α, β, and γ (we’re using Greek letters just to add to the variety of symbols used.) Note that none of α, β, and γ have to be primitive, they just denote some proposition, whether those propositions be simple, complex, or anywhere in between.

Now consider the following argument:

(p1 ∧ p2) → c

where

p1:α → β
p2:β → γ
c:α → γ

We start by looking at a truth table for the propositions and the premises. We can fill this table out, one column at a time starting from the left-most blank column, and going right:

p1p2p1 ∧ p2c(p1 ∧ p2) → c
αβγα → ββ → γ(α → β) ∧ (β → γ)α → γ[(α → β) ∧ (β → γ)] → (α → γ)
00011111
00111111
01010011
01111111
10001001
10101011
11010001
11111111

As such, it appears that the argument

[(α → β) ∧ (β → γ)] → (α → γ)

is valid. Therefore, if we ever run into a situation where we know that (α → β) and that (β → γ), then we know that (α → γ) as well (where α, β, and γ represent arbitrary propositions.)