Subsets

A set can contain wide variety of objects. They can contain objects that most people interact with on a daily basis. They can consist of automotive parts that can be used to service a 1967 Camaro, tools used to carve statues out of wood, or art supplies needed to paint a picture. Likewise, they can contain a wide variety of mathematical objects like numbers, shapes, or axioms.

Sometimes, we may only care about some of the objects in a set. For example, we may only be interested in automotive parts needed to service a car’s head lights, or we may only be interested in art supplies needed for a fresco painting. Regardless, we are able to build a lot of structure by simply constructing new sets from old ones by simply restricting what elements are included in the new set. Here, we explore such relationships between these kinds of sets.

Starting with a Base Set

If we are interested in selecting only some of the elements from a set, we’ll need to know what the original, or underlying set contains. The idea is exactly the same from Section 7 of Chapter 1. There, we defined what the Universe of Discourse is. Using our new terminology, we recognize that for an open proposition, a Universe of Discourse (or simply Universe) is the set of all values we allow to be substituted in for the variables of a propositional function.

It’s the exact same situation here. We even commonly use the same script letter 𝒰 to denote the base set, though we can still use any symbol we want.

Example 3.2.1

Suppose we were presented with the following set:

X = { x | 1 ≤ x ≤ 10 }.

Is 1.5 ∈ X?

It’s hard to tell without knowing what kinds of numbers we even want included in this set. Does it include all the real numbers between 1 and 10 inclusive? Or does it only include whole numbers from 1 to 10 inclusive?

Let’s remedy the situation by stating that set X is only going to copy elements from the set 𝒰 of all integers. Then we know that

X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

Of course, since we now have an established universe, we can simply write

X = { x | 1 ≤ x ≤ 10 }

without any ambiguity.

We could also write something like

X = { x ∈ 𝒰 | 1 ≤ x ≤ 10 }

or we could even write

X = { x | 1 ≤ x ≤ 10 and x ∈ 𝒰 }.

Because we’ve established some base set, all these different ways of describing a set yield the exact same set X of integers between 1 and 10 inclusive.

As such, since we now know what kinds of numbers we’re including in X, we can definitively say that

1.5 ∉ X.

Example 3.2.2

Reconsider Example 3.2.1 where we redefine 𝒰 to be

𝒰 = { x | x is an even integer }.

In this case, since the allowable elements are the even integers, we have that

X	=	{ x \| 1 ≤ x ≤ 10 }
	=	{ 2, 4, 6, 8, 10 }

Alternatively, we could define 𝒰 to be the set of all perfect squares:

𝒰	=	{ x \| x is a perfect square }
	=	{ 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, … }

If 𝒰 was the set of all perfect squares, then we would have that

X	=	{ x \| 1 ≤ x ≤ 10 }
	=	{ 1, 4, 9 }

Subsets

The definition of a subset is closely related to what we’ve discussed so far in this section. We start with a universe of discourse, and then construct a set using only elements from that universe. We could go even further by constructing a third set by only taking elements from that second set.

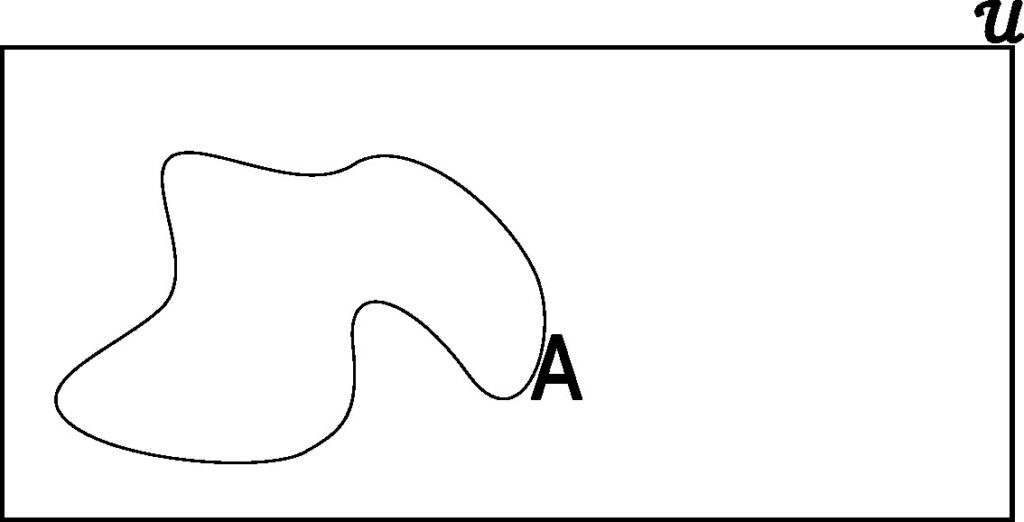
Figure 3.2.1: In (a), we start with our universal set, which we depict graphically as just a large rectangle encompassing a large area. Here, we denote the universal set 𝒰. In (b), we draw a boundary around part of the area enclosed by 𝒰. That enclosed area denotes a subset, which we refer to as A. Notice that the area enclosed by A is still enclosed by 𝒰, meaning anything that is part of A, is also a part of 𝒰.

Subset

If A and B are sets constructed using only elements of some given universe 𝒰, we say that A is a subset of B if (and only if) every element of A is also an element of B. When A is a subset of B, we can write

A ⊆ B.

Logically, we would write

∀x [x ∈ A ⟹ x ∈ B].

Alternatively, if A is not a subset of B, we can write

A ⊈ B.

Notice that the above definition uses a universally quantified logical implication. This offers us a chance to review logical implications, and what they mean in the context of sets and subsets. Since there is a logical implication involved, that means that the proposition

x ∈ A → x ∈ B

is always true; thus, when we have that A ⊆ B, there are only three scenarios:

x ∈ A	x ∈ B	x ∈ A → x ∈ B	Interpretation
0	0	1	The element referred to by x is in neither A nor B.
0	1	1	The element referred to by x is not in A, but is in B.
1	0	0	The element referred to by x is in A, but not in B, meaning A ⊈ B.
1	1	1	The element referred to by x is in both A and B.

We colored the third row red because since we are asserting that A ⊆ B, the scenario represented by the third row can’t happen.

Example 3.2.3

Consider the universe ℕ of all positive integers

{ 1, 2, 3, 4, 5, 6, 7, 8, 9, … }.

Now consider the following sets:

X	=	{ x \| x² ≤ 100 }
	=	{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

Y	=	{ y \| y² ≤ 37 }
	=	{ 1, 2, 3, 4, 5, 6 }

In order for Y ⊆ X, we need to verify that

∀n [n ∈ Y ⟹ n ∈ X].

If n refers to anything that is not in Y, then n ∉ Y, meaning

n ∈ Y = 0

and hence

n ∈ Y → n ∈ X = 1

so we don’t have to worry about checking elements that are not in Y. Let’s examine each element in Y, and see if it’s in X as well:

n	n ∈ Y	n ∈ X	n ∈ Y → n ∈ X
1	1	1	1
2	1	1	1
3	1	1	1
4	1	1	1
5	1	1	1
6	1	1	1

The column representing proposition

n ∈ Y → n ∈ X

has all 1s for each of the desired numbers. Hence it’s a tautology, meaning it’s a logical implication and we can write

n ∈ Y ⟹ n ∈ X.

Thus, we have shown that Y is a subset of X and we can write

Y ⊆ X.

It’s also worth noting that we also have that

X ⊆ ℕ

Y ⊆ ℕ

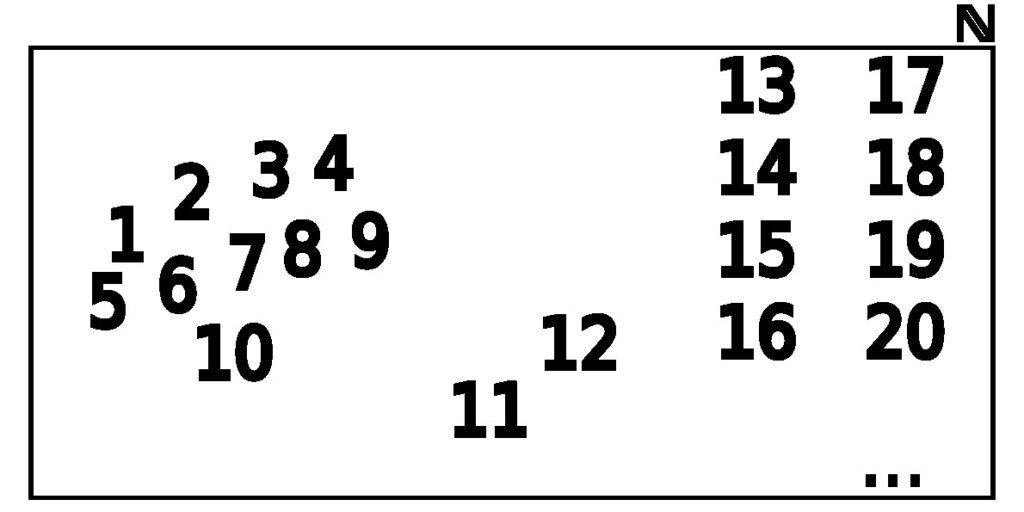
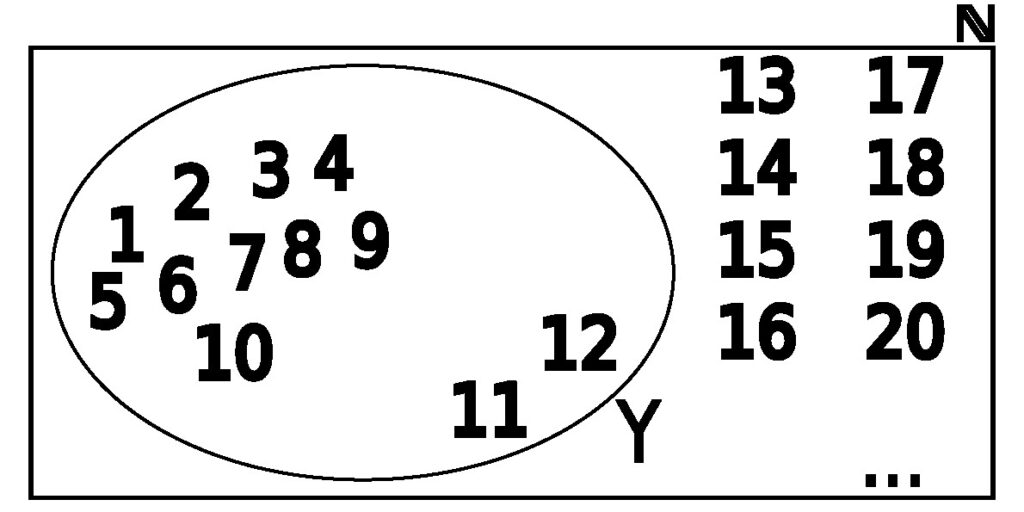
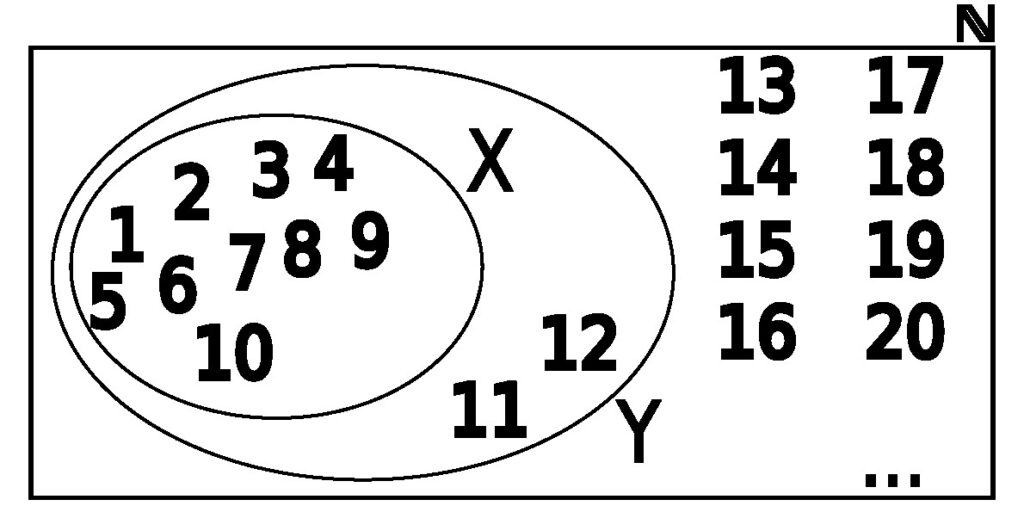
Figure 3.2.2: In (a), we show the set ℕ as defined in Example 3.2.4. In (b), we show the set Y as defined in Example 3.2.4. Notice that it is entirely enclosed within ℕ. In (c), we also show the set X. This is a graphical depiction of the subset relationships between X, Y, and ℕ where

X ⊆ Y ⊆ ℕ

Example 3.2.4

Consider the universe ℕ of all positive integers

{ 1, 2, 3, 4, 5, 6, 7, 8, 9, … }.

Now consider the following sets:

X	=	{ x² \| x² ≤ 100 }
	=	{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

Y	=	{ y² \| y² ≤ 145 }
	=	{ 1, 2, 3, 4, 5, 6, 7, 8,9 , 10, 11, 12 }

In order for Y ⊆ X, we need to verify that

∀n [n ∈ Y ⟹ n ∈ X].

However, suppose we substituted 11 in for n. We see that

11 ∈ Y

11 ∉ X

Meaning that

11 ∈ Y → 11 ∈ X = 0

and so we don’t have a logical implication, meaning we have that Y ⊈ X.

However, we do have that X ⊆ Y.

Remember that a subset is a set in its own right, it just happens that all of that subset’s elements are also contained within some other set as well.

The Empty Set

Just because we can put just about anything in a set, that does not mean we need to have something in a set. There is a special and unique kind of set that has no elements in it at all!

Empty Set, Null Set

The empty set is the unique set containing no elements at all.

The empty set is sometimes referred to as the null set, and is often symbolized by ∅.

The empty set is a very special set and occurs throughout all of set theory, but it does have some interesting quirks that are somewhat weird at first, but become more natural as we work more and more with this kind of set.

First, note that because it is a set containing nothing, we can write

∅ = { }.

There is absolutely nothing written in between the curly braces, thus we have for example that

∅ ≠ { 0 }.

Above, we wrote a single number in between the braces, and since { 0 } is a set containing one item, it is not equal to the empty set.

The second thing to note is that a set can have the empty set as one of it’s elements:

S = { ∅ }.

Because S is a set containing one element (that element itself being a set), we have that

|S| = 1.

Thus, since S contains at least one element, it is not the same thing as the empty set, even though it’s the set containing the empty set:

S ≠ ∅.

Comparing S to ∅, since ∅ contains no elements, we have that

|∅| = 0.

If we substitute { ∅ } in for S, we see that

{ ∅ } ≠ ∅.

The Empty Set is Always a Subset

Recall the definition of subset, which states that A ⊆ B when every element in A is also an element of B. In other words,

n ∈ A → n ∈ B

is always true.

We use that definition, as well as the definition of the Empty Set in our next theorem:

Theorem 3.2.1

For any universe 𝒰, let A be any set such that A ⊆ 𝒰.

∅ ⊆ A

Proof

Let x be any arbitrary element from 𝒰.

Because ∅ contains no elements, it is impossible for x ∈ ∅, thus it is always true that

x ∈ ∅ = 0.

Notice that since x ∈ ∅ is always equal to 0, we have that

x ∈ ∅ → x ∈ A	=	0 → x ∈ A
	=	1

Notice that it does not matter whether x is an element of A or not because the hypothesis of the implication

x ∈ ∅

is always false, meaning that the overall implication always evaluates to true, meaning we have that

x ∈ ∅ ⟹ x ∈ A.

Thus, we have that

∅ ⊆ A

as desired.

Notice that in Theorem 3.2.1, we did not have any special requirements for set A, it just had to be an arbitrary set created from some universe 𝒰. Thus, by the Rule of Universal Generalization, since A was an arbitrary set, and we have that ∅ ⊆ A, then ∅ must be a subset of every possible conceivable set, even including the universe 𝒰 itself!

Example 3.2.5

By Theorem 3.2.1, for set

A = { 1, 2, 3 },

we have that

{ } ⊆ A.

Every Set is a Subset of Itself

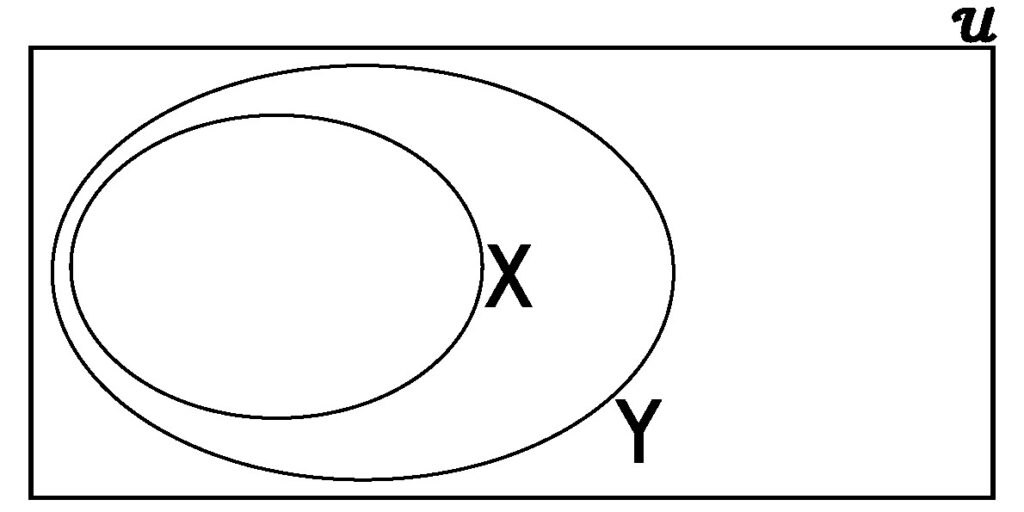
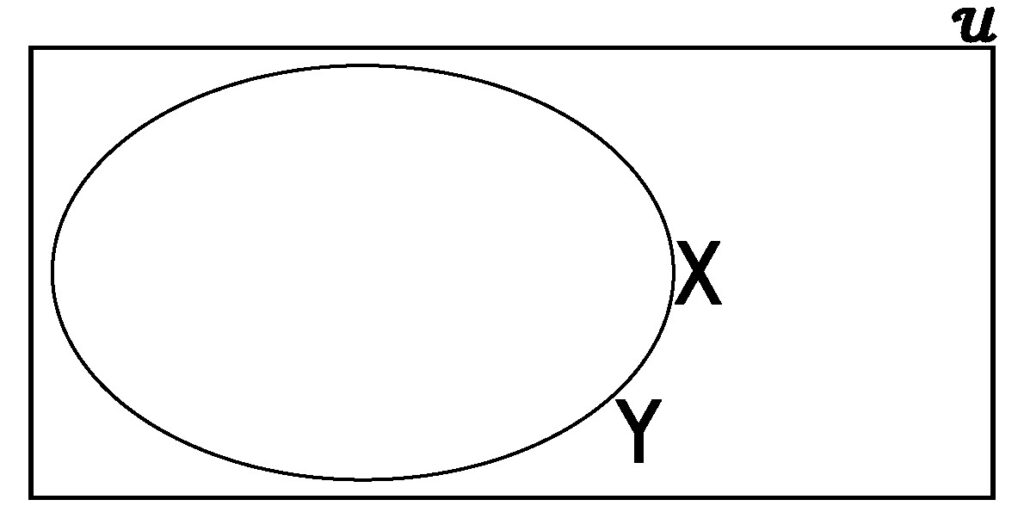
Figure 3.2.3: In (a), we show two sets X and Y that are both subsets of some universal set 𝒰. Here, we see that X ⊆ Y, where there is space enclosed in set Y that is not enclosed in X, meaning that Y has elements that are not in Y. In (b), we see that even though X and Y refer to the same set, we still have that X ⊆ Y because anything enclosed by X is also enclosed by Y.

Consider the proposition

x ∈ A → x ∈ A.

Since the same primitive proposition (x ∈ A) is on both sides of the implication, we have only two scenarios to consider:

x ∈ A	x ∉ A
x ∈ A → x ∈ A = 1 → 1 = 1	x ∈ A → x ∈ A = 0 → 0 = 1

Both situations yield a truth value of one, meaning it’s a logical implication. This yields the following theorem:

Theorem 3.2.2

For any universe set 𝒰, and set A ⊆ 𝒰, we have that

A ⊆ A.

Proof

Consider some arbitrary element x from 𝒰.

If we have that x ∈ A, then obviously x ∈ A (because we literally just considered that case.)

Thus, since every element contained in A is (obviously) contained within A, the definition of subset tells us that

A ⊆ A

as desired.

Example 3.2.6

Consider the set

B = {x, y, z}

where x, y, and z are not being used as variables, but are simply the 24^th, 25^th, and 26^th letters of the alphabet. By Theorem 3.2.2, we have that

{x, y, z} ⊆ {x, y, z}.

Proper Subsets

Of course, when we assert that A ⊆ B, all we’re saying is that whenever x ∈ A, then we also have that x ∈ B. However, this definition does not say whether or not every single element of B must be contained within A. We have a special term to describe when A is a subset of B, but B has elements not contained within A.

Figure 3.2.4: Here, because Y encloses some amount of area that is not enclosed by X, we know that every element in X is also in Y, but Y has elements that are not in X, hence X is a proper subset, and so we can write X ⊂ Y.

Proper Subset

Consider two sets A and B.

A is said to be a proper subset of B if (and only if) every element contained within A is also in B, but B has at least one element that is not contained within A. We denote this by writing

A ⊂ B.

Logically, we would write this like

∀a ∈ A [a ∈ B] ∧ ∃b ∈ B [b ∉ A]

Example 3.2.7

Consider the following sets:

M = { x | x is an odd integer }

N = { x | x is an integer }.

Because every odd integer integer is a specific kind of integer, that would mean that every element contained within M is also an element of N, hence we can write

M ⊆ N.

However, notice that 0 ∈ N, but that 0 ∉ M, meaning set N has at least one number that is not contained within M, meaning M is a proper subset of N, and so we can also write

M ⊂ N.

Notice that by Example 3.2.7 that for any two subsets A and B, it is possible for both

A ⊆ B

A ⊂ B

to be true. However, that is not always the case as demonstrated by the next example.

Example 3.2.8

Consider the set

Ψ = { a, b, c, 1, 2, 3, x, y, z, {1, 2, 3} }.

By Theorem 3.2.2, we clearly have that Ψ ⊆ Ψ.

However, notice that we don’t have Ψ ⊂ Ψ. Obviously any element contained within Ψ is going to be contained within Ψ (that is tautologically true.) However, there are no elements within Ψ that are not also contained within Ψ (again, this is tautologically true.)

Thus, it is not the case that Ψ is a proper subset of itself (no set can be a proper subset of itself.)

Now consider the following set:

Ω = { b, 1, z, {1, 2, 3} }.

We can clearly see that every element contained within Ω is also an element of Ψ:

n	n ∈ Ψ
b	1
1	1
z	1
{1, 2, 3}	1

Thus, we can write Ω ⊆ Ψ.

Notice though that a ∈ Ψ, but that a ∉ Ω, and so we have that Ω ⊂ Ψ as well.

Based on the previous two examples, it seems as if we know that A ⊂ B, we also know that A ⊆ B. Let’s formally show this is the case.

Theorem 3.2.3

If A ⊂ B, then A ⊆ B.

Proof

Since we know that A ⊂ B, we have by definition that for any element a in A, a will also be in B. Thus, by definition, we have that A ⊆ B as well.

Notice that if we know A ⊆ B, then we don’t automatically know that A ⊂ B. For example, we have that A ⊆ A, but A ⊄ A.

The Book ofFoundational Mathematics

Quick Links

Subsets

Starting with a Base Set

Example 3.2.1

Example 3.2.2

Subsets

Subset

Example 3.2.3

Example 3.2.4

The Empty Set

Empty Set, Null Set

The Empty Set is Always a Subset

Theorem 3.2.1

Proof

Example 3.2.5

Every Set is a Subset of Itself

Theorem 3.2.2

Proof

Example 3.2.6

Proper Subsets

Proper Subset

Example 3.2.7

Example 3.2.8

Theorem 3.2.3

Proof

The Book of
Foundational Mathematics