Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
The Book of
Foundational Mathematics
1 Propositional Logic
2 Arguments and Proof
- The Structure of Basic Arguments
- Rules of Inference
- Using the Rules of Inference
- Logically Equivalent Arguments
- Invalid Arguments
- Universal Specification
- Universal Generalization
- Axioms, Definitions, Theorems, and Proofs
- Proof Technique: Direct Proofs
- Proof Technique: Indirect Proofs
- Proof Technique: Contradiction
- Mistakes in Proofs
- Proof Technique: Equivalence
4 Relations and Functions
Appendix
Set Partitions
When working with a set of related objects, we may want to split that set up into smaller, more manageable sets.
For example, we may want to split up the integers based on parity: even integers, and odd integers. When dealing with the real numbers, we may want to split them up into three separate sets: the positive real numbers, the negative real numbers, and the number 0. One more example may be the positive rational numbers, where we split them up based on how big they are. We may have all of the positive rational numbers less than 1 in one set, and all of the positive rational numbers greater than or equal to 1 in the other set.
No matter how we split up a set, we’ll want to make sure that all elements of the original set are accounted for in one of the smaller subsets we form.
Partitioning a Set
In the introduction to this section, we mentioned three examples of how we may split a large set into smaller subsets, making sure every element with the original set is in one of the subsets. A partition of a set creates these subsets, while making sure that every element is accounted for, however, the word partition also invokes the idea of separation: no two sets should share any elements. The following definition of partition offers something more precise.
Partition
Consider some set A ⊆ 𝒰 along with some index set I.
For each i ∈ I, let Ai ⊆ A such that Ai ≠ ∅. Then the set
{ Ai | i ∈ I }
is called a partition of A if (and only if) the following two conditions are satisfied:
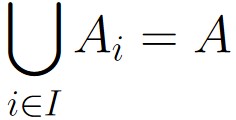
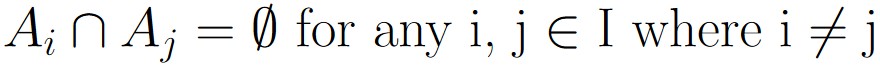
Note that none of the sets in the partition can be empty. The whole point of forming a partition is take elements from the original set and put them into a subset.
Example 3.7.1
Consider the the following set of numbers
A = { 0, 1, -1, 2, -2, 3, -3, 4, -4 }
If we want to partition this set, we need to form non-empty subsets that are all disjoint, and such that all elements in A are in one of the subsets.
Here’s one way to partition A:
| A1 | = | { 0, 1 } |
| A2 | = | { -1, 2, -2 } |
| A3 | = | { 3, -3, 4, -4 } |
Notice that we didn’t start with the index set
I = { 1, 2, 3 }
Instead, we formed the subsets first, and then indexed them. Of course, we should check to see if the conditions specified in the definition are met:
A1 ∪ A2 ∪ A3 = A
| A1 ∪ A2 ∪ A3 | = | { 0, 1 } ∪ { -1, 2, -2 } ∪ { 3, -3, 4, -4 } |
| = | A |
This means that every element from A was accounted for. Now we check to see if all the subsets are disjoint:
| A1 ∩ A2 | = | { 0, 1 } ∩ { -1, 2, -2 } |
| = | ∅ |
| A1 ∩ A3 | = | { 0, 1 } ∩ { 3, -3, 4, -4 } |
| = | ∅ |
| A2 ∩ A3 | = | { -1, 2, -2 } ∩ { 3, -3, 4, -4 } |
| = | ∅ |
Both conditions have been met, so this is a legitimate partition of A.
Example 3.7.2
There are other ways to partition the set
A = { 0, 1, -1, 2, -2, 3, -3, 4, -4 }
One such way to partition the set is with the following:
| X1 | = | { 0, 4 } |
| X2 | = | { -1 } |
| X3 | = | { 1, 2 } |
| X4 | = | { -2, -3, -4 } |
| X5 | = | { 3 } |
Notice that we didn’t use the letter A for the names of these subsets. The important thing is the content of the subsets themselves, not the name given to the subsets. As long as the two conditions are met, the collection of sets form a partition. We could also put every element in A into it’s own subset like so:
| Y1 | = | { 0 } |
| Y2 | = | { 1 } |
| Y3 | = | { -1 } |
| Y4 | = | { 2 } |
| Y5 | = | { -2 } |
| Y6 | = | { 3 } |
| Y7 | = | { -3 } |
| Y8 | = | { 4 } |
| Y9 | = | { -4 } |
Yet another partition we could form is just by taking the entire set itself:
Z = { 0, 1, -1, 2, -2, 3, -3, 4, -4 }
Since there are no other sets in this partition, it is trivially true that the union of all the sets form A. Furthermore, since there are no other sets in the partition, it is trivially true that all sets in the partition are disjoint.
Examples of Partitions
Example 3.7.3
As mentioned in the introduction, one thing we can do is split up the integers into two subsets: one containing the even integers, and a second subset containing the odd integers.
| A | = | { 0, 2, -2, 4, -4, 6, -6, … } |
| B | = | { 1, -1, 3, -3, 5, -5, 7, -7, … } |
Here, we didn’t use the same letter for the subset names, nor did we use indices. Again, the names of the subsets is not important. What’s important is knowing that all subsets are mutually disjoint, and that all elements from the original set are accounted for.
Example 3.7.4
One way to partition the real numbers ℝ is into three subsets: the subset of all positive real numbers greater than 0, the subset of all negative real numbers less than 0, and finally the subset containing just the number 0.
| X | = | { x ∈ ℝ | x < 0 } |
| Y | = | { 0 } |
| Z | = | { x ∈ ℝ | x > 0 } |
Some numbers that are in X include -π, -12.3372, and -√2.
Some numbers in Z include 1.2345, 12, and π * π.
Example 3.7.5
As one more example, we could partition the positive rational numbers into two separate subsets.
| A | = | { a/b | a ∈ {0, 1, 2, 3, …} ∧ b ∈ {1, 2, 3, …} ∧ a/b < 1} |
| B | = | { a/b | a ∈ {0, 1, 2, 3, …} ∧ b ∈ {1, 2, 3, …} ∧ a/b ≥ 1} |