Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124

When we form the Cartesian Product A ✕ B, we are essentially pairing up every element from A up with an element from B. However, we may not want to associate each element from A to every element in B. Instead, we may only want certain elements to pair up because there is some relationship we want to observe.
The way we pair up only certain elements from A to certain elements of B is by taking a subset of A ✕ B. These kinds of subsets are yet another fundamental structure that appear throughout all of mathematics.
As stated in the introduction to this section, here we are going to consider subsets of the Cartesian Product of two sets A and B.
A subset of A ✕ B is called a relation, more specifically it is called a (binary) relation from A to B, and is normally denoted with the symbol ℛ, which is just a stylized upper case R.
For a relation ℛ derived from A ✕ B, whenever we have that
(a, b) ∈ ℛ
we can instead write
a ℛ b
to specify that a is related to b.
The reason why the word binary was used in the definition is because there were two sets being considered: A, and B. Let’s look at a few examples.
Consider the sets
| A = { 1, 2, 3, 4, 5 } | B = { 2, 4, 6, 8, 10 } |
Forming the Cartesian Product, we see that
| A ✕ B | = | { | (1, 2), | (1, 4), | (1, 6), | (1, 8), | (1, 10), | |
| (2, 2), | (2, 4), | (2, 6), | (2, 8), | (2, 10), | ||||
| (3, 2), | (3, 4), | (3, 6), | (3, 8), | (3, 10), | ||||
| (4, 2), | (4, 4), | (4, 6), | (4, 8), | (4, 10), | ||||
| (5, 2), | (5, 4), | (5, 6), | (5, 8), | (5, 10) | } |
Now we can consider a few different relations on this Cartesian Product.
We can just include some arbitrary, randomly selected elements without any rhyme or reason:
ℛ = { (1, 2), (3, 2), (2, 4), (3, 4), (1, 6), (1, 8), (2, 8), (5, 8), (5, 10) }
For our first relation, we see that the number 1 (taken from A) is related to a few different numbers from B:
| 1 ℛ 2 | 1 ℛ 6 | 1 ℛ 8 |
We also see that 3 (taken from A) is related to some of the numbers from B:
| 3 ℛ 2 | 3 ℛ 4 |
The numbers 2 and 5 from A are also related to a few of the numbers from B:
| 2 ℛ 4 | 2 ℛ 8 |
| 5 ℛ 8 | 5 ℛ 10 |
Reconsider the Cartesian Product
| A ✕ B | = | { | (1, 2), | (1, 4), | (1, 6), | (1, 8), | (1, 10), | |
| (2, 2), | (2, 4), | (2, 6), | (2, 8), | (2, 10), | ||||
| (3, 2), | (3, 4), | (3, 6), | (3, 8), | (3, 10), | ||||
| (4, 2), | (4, 4), | (4, 6), | (4, 8), | (4, 10), | ||||
| (5, 2), | (5, 4), | (5, 6), | (5, 8), | (5, 10) | } |
from Example 4.3.1.
This time, instead of picking arbitrary elements from A ✕ B, let’s choose ordered pairs that satisfy some rule.
One relation we could take is
(a, b) ∈ ℛ1 if b = 2a
One such ordered pair is (a, b) = (2, 4) because a = 2, b = 4, and
b = 4 = 2(2) = 2a
Another such ordered pair is (1, 2) because 2 is twice as much as 1. We can list all of the desired ordered pairs:
ℛ1 = { (1, 2), (2, 4), (3, 6), (4, 8), (5, 10) }
Another relation we could take is
ℛ2 = { (a, b) | a = 3 ∨ b = 2 }
where the ordered pairs we are interested in either have 3 as the first element, 2 as the second element, or both. This gives us that
| ℛ2 | = | { (a, b) | a = 3 ∨ b = 2 } |
| = | { (3, 2), (3, 4), (3, 6), (3, 8), (3, 10), (1, 2), (2, 2), (4, 2), (5, 2) } |
Yet another kind of relation we could take is
ℛ3 = { (a, b) | a = 3 ∧ b = 2 }
Here, we need ordered pairs where a = 3 and b = 2. Looking at A ✕ B, we see there is only one ordered pair satisfying the requirement:
| ℛ3 | = | { (a, b) | a = 3 ∧ b = 2 } |
| = | { (3, 2) } |
Looking at one more relation we can take, consider the following:
ℛ4 = { (a, b) | a = 3 ∧ a = 5 }
There are no ordered pairs in A ✕ B such that the first element is simultaneously 3 and 5. Thus we have that
ℛ4 = { } = ∅
So ℛ4 is an empty relation.
Suppose a college is trying to come up with a course roster, and so far has the following two sets:
C = { Calculus, Linear Algebra, Drawing, American History }
P = { Smith, Williams, Harrison, Sanchez }
where C is a set of classes, and P is a set of professors.
Of all the ways to assign a professor to teach a class (which can be seen by computing C ✕ P), we instead want to consider assignments where math professors teach math classes, art professors teach art classes, and history professors teach history classes.
Suppose Smith and Sanchez are math professors, Williams is a history professor, and Harrison is a literature professor, then one assignment could be
ℛ1 = { (Calculus, Sanchez), (Linear Algebra, Smith), (American History, Williams) }
Unfortunately in this scenario, there are no professors available to teach Drawing, so the college will need to continue it’s search for such a professor.
Instead, suppose we knew that
Smith is a math professor, Sanchez is an art professor, Harrison is a history professor, and Williams is a literature professor. Then we could make the following assignments:
ℛ2 = { (Calculus, Smith), (Linear Algebra, Smith), (Drawing, Sanchez), (American History, Harrison) }
Here, Smith has to teach two classes, whereas Williams is not assigned to teach any classes.
Just like we can take a Cartesian Product of a set with itself as in A ✕ A, we can also take subsets of A ✕ A to form relations. In this case we would say that ℛ is a (binary) relation on A. Again, we use the word binary to describe the fact that there are two sets being used in the Cartesian Product.
Consider the set
A = { -2, -1, 0, 1, 2 }
The Cartesian Product is thus
| A ✕ A | = | { | (-2, -2), | (-2, -1), | (-2, 0), | (-2, 1), | (-2, 2), | |
| (-1, -2), | (-1, -1), | (-1, 0), | (-1, 1), | (-1, 2), | ||||
| (0, -2), | (0, -1), | (0, 0), | (0, 1), | (0, 2), | ||||
| (1, -2), | (1, -1), | (1, 0), | (1, 1), | (1, 2), | ||||
| (2, -2), | (2, -1), | (2, 0), | (2, 1), | (2, 2) | } |
Consider the relation
(a1, a2) ∈ ℛ if a1 < a2
This is the “less than relation”, so instead of using ℛ, we could instead use the symbol <. This means that instead of writing
-1 ℛ 0,
we could instead write
-1 < 0
which coincides with commonly used mathematical notation. Here, we see that
ℛ = < = { (-2, -1), (-2, 0), (-2, 1), (-2, 2), (-1, 0), (-1, 1), (-1, 2), (0, 1), (0, 2), (1, 2) }
Note that we are using the symbol < both as a comparison operator (its normal usage), and as a name for a set, the latter of which is very unusual, and tends to be avoided.
Consider the set
☆ = { 0, 0.3, 0.7, 1, 1.5, 1.7, 2, 2.1, 2.11 }
of real numbers.
We could consider the relation
ℛ = { (x, y) ∈ ☆ ✕ ☆ | y = ⌈x⌉ }
where the second element is simply the ceiling value of the first element. For example, because ⌈0.3⌉ = 1, we have that
0.3 ℛ 1.
We thus have that
| ℛ | = | { (x, y) ∈ ☆ ✕ ☆ | y = ⌈x⌉ } |
| = | { (0, ⌈0⌉), (0.3, ⌈0.3⌉), (0.7, ⌈0.7⌉), (1, ⌈1⌉), (1.5, ⌈1.5⌉), (1.7, ⌈1.7⌉), (2, ⌈2⌉) } | |
| = | { (0, 0), (0.3, 1), (0.7, 1), (1, 1), (1.5, 2), (1.7, 2), (2, 2) } |
Notice that since 3 ∉ ☆, we are not able to put (2.1 3) and (2.11, 3) into ℛ because
| (2.1 3) ∉ ☆ ✕ ☆ | (2.11, 3) ∉ ☆ ✕ ☆ |
and as such can’t possibly be in any subset of ☆ ✕ ☆.
There is absolutely nothing stopping us from considering subsets of Cartesian Products involving three sets.
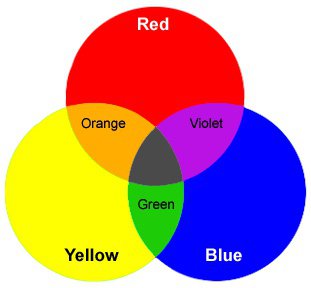
Figure 4.3.1: This Venn Diagram shows how pigment colors mix together to form new colors.
Consider the set of primary pigment colors and secondary pigment colors
| P = {Red, Yellow, Blue} | S = { Orange, Green, Violet } |
We can form a relation from the Cartesian Product
P ✕ P ✕ S
by considering triples where the first two elements can be mixed together to get the third color. As such, this is the relation
ℛ1 = { (Red, Yellow, Orange), (Red, Blue, Violet), (Yellow, Blue, Green) }.
We could organize this relation by making it more obvious which colors mix together to form the third by using parenthesis:
(P ✕ P) ✕ S
From this, we could form the relation ℛ2 ⊆ (P ✕ P) ✕ S by taking
ℛ2 = { ((Red, Yellow), Orange), ((Red, Blue), Violet), ((Yellow, Blue), Green) }
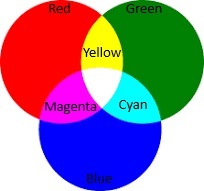
Figure 4.3.2: This Venn Diagram shows how light-based colors can be mixed together to form new colors.
Just like pigment-based colors can be mixed together to form new colors, light-based colors can also be combined. Consider the sets
| P = {Red, Green, Blue} | S = { Yellow, Cyan, Magenta } |
Here, we can form the relation from
P ✕ P ✕ S
in a similar way we did in Example 4.3.6:
ℛ1 = { (Red, Green, Yellow), (Green, Blue, Cyan), (Red, Green, Magenta) }
Once again, we could also organize the relation a little bit by making it clear which colors are being combined by considering the relation ℛ2 ⊆ (P ✕ P) ✕ S:
ℛ2 = { ((Red, Green), Yellow), ((Green, Blue), Cyan), ((Red, Green), Magenta) }