Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124

All of the propositions we’ve dealt with so far had definite truth values. For example,
“Thomas Jefferson was the second president of the United States of America”
is a proposition that is known to be false. A statement such as
“2 + 2 = 4 or 2 + 2 = 5”
is a compound statement that is true.
However, a statement such as
“n is 1 more than a multiple of 3”
is not a proposition because we don’t know if it is true or false. We would need to know the value of n in order to reach such a conclusion. For example, the statement is false when n = 5, but it is true when n = 16. Here, we’ll deal with sentences involving variables.
Consider the statement
“x + 3 = 8.”
Here, we are not asking what value of x solves the equation (we could, but that is not our focus.) Instead, what we are going to ask is whether, given a specific value of x, the statement is a true proposition or a false proposition.
We start by modeling the statement using a letter like we’ve done up to this point, but we also use () to denote the variable x:
p(x): “x + 3 = 8.”
We can substitute values in for x to get different propositions.
| p(5): | “5 + 3 = 8” |
| p(3): | “3 + 3 = 8” |
| p(-4.73): | “-4.73 + 3 = 8” |
| p(Thomas Jefferson): | “Thomas Jefferson + 3 = 8” |
We can evaluate some of these propositions.
| p(5): | true |
| p(3): | false |
| p(-4.73): | false |
The last proposition has an undefined truth value because we do not currently have a way to add the quantities “Thomas Jefferson” and 3 together to produce a new value.
p(Thomas Jefferson): undefined
Consider the statement
p(x): “x was the 30th president of the United States of America.”
We can evaluate this statement with many values substituted in for x:
| p(James K. Polk): | 0 |
| p(Cecil Rhodes): | 0 |
| p(Grover Cleveland): | 0 |
| p(Calvin Coolidge): | 1 |
| p(Bill Clinton): | 0 |
For this open statement, it may make sense to try other kinds of inputs:
p(3): 0.
Of course, a number is not going to a president of the United States of America, so we could argue that p(3) would be false.
On the other hand, maybe we should say p(3) is undefined.
An open statement is any declarative sentence that has one or more variables and thus is not a proposition, but becomes a proposition after values are substituted for all variables in the sentence.
The example from the introduction, and from Example 1.7.1 are both open statements because they are declarative sentences with variables. Their truth value can be determined after values are substituted in the sentences.
Just like with normal propositions, we write
p(x) = 0
if the value of x makes p(x) a false proposition, and we write
p(x) = 1
if the value of x makes p(x) a true proposition.
A statement p(x) which represents an open statement with variable x is often called a propositional function.
For a propositional function p(x), we write
p(x) = false
if the supplied value of x makes p(x) a false proposition, and we write
p(x) = true
if the supplied value of x makes p(x) a true proposition.
A propositional function can depend on many variables, which is demonstrated by the next example.
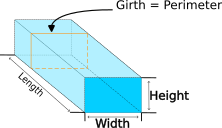
Figure 1.7.1:The girth of a box is the perimeter of the rectangular cross section. We need the sum of the length and girth to be no more than 108 inches.
The U.S. Postal Service will only ship packages in a box that meets certain requirements. According to the U.S. Postal Service webpage found here, the sum of the box’s length and girth must not exceed 108 inches. The U.S. Postal Service includes guidelines on how to measure a box’s girth here.
According to the second webpage, the girth is essentially the perimeter of the box’s rectangular cross section. Let ℓ, w, and h represent a box’s length, width, and height respectively. From geometry, we know that the perimeter of a box’s rectangular cross section is given by 2w + 2h. Thus, in order to comply with USPS shipping requirements, we need to make sure that
ℓ + 2w + 2h ≤ 108 inches.
We can model this situation using a propositional function with three variables:
s(ℓ, w, h): ℓ + 2w + 2h ≤ 108 inches.
Can we ship a box with dimensions ℓ = 32 inches, w = 16 inches, and h = 18 inches? We have that
| (32 inches) + 2(16 inches) + 2(18 inches) | = | 32 inches + 32 inches + 36 inches |
| = | 100 inches | |
| ≤ | 108 inches |
Because 100 inches ≤ 108 inches, we have that s(32, 16, 18) = 1, meaning s(32, 16, 18) is a true proposition. In the context of this problem, we can ship a box with length 32 inches, width 16 inches, and height 18 inches.
However, s(20, 18, 30) = 0 because
| (20 inches) + 2(18 inches) + 2(30 inches) | = | 20 inches + 36 inches + 60 inches |
| = | 116 inches | |
| ≰ | 108 inches |
As such, we can’t ship a box with length 20 inches, width 18 inches, and height 30 inches with USPS.
Let’s reconsider Example 1.7.2.
For the propositional function
p(x): “x was the 30th president of the United States of America.”
We saw that we could argue that p(3) was either false or undefined. We could eliminate this ambiguity by specifying what kinds of values we are allowed to input into p(x). If a value a is allowed to be input into p(x), then either p(a) is true or false. However, if b is a value not allowed to be put into p(x), then p(b) would be undefined.
Let’s restrict the values allowed to be put into the propositional function p(x) to proper names. This would mean that values such as “James K. Polk”, “Cecil Rhodes”, “Grover Cleveland”, “Calvin Coolidge”, and “Bill Clinton” can be substituted for x in p(x) and would yield either true or false.
However, when putting in a value for x that is not a proper name, we will say that p(x) will be undefined. Since 3 is not a proper name, p(3) would have an undefined value. Thus, we are no longer able to say that p(3) is false, even if we knew that 3 was not the 30th president of the United States of America. This is what allows us to remove any ambiguity.
We could further restrict the inputs to be names of U.S. presidents only, instead of just any proper name. If that were the case, then we would say that p(Cecil Rhodes) is undefined because “Cecil Rhodes” is not the name of any U.S. president (at least at the time of this writing.)
Reconsider the propositional function
p(x): “x was the 30th president of the United States of America.”
Suppose we restrict the allowable values to be names of U.S. presidents except “Calvin Coolidge.” Then p(Calvin Coolidge) would be undefined. Substituting any other U.S. president’s name would yield a truth value of 0, since only Calvin Coolidge was the 30th U.S. president. If we were to do this, then p(x) would never yield a truth value of 1. It would only ever yield values of 0, or undefined.
Note that this would also mean that something such as
p(The president between Warren G. Harding and Herbert Hoover)
would also be undefined because no U.S. president was ever named “The president between Warren G. Harding and Herbert Hoover.”
Restricting the allowable names to be those of Spanish monarchs would also either yield truth values of 0, or undefined values (when an input is not the name of a Spanish monarch.)
We could also restrict the allowable values to be even integers. Again p(x) would always either be false, or undefined.
Reconsider the propositional function
p(x): “x + 3 = 8.”
If we restrict our inputs to be integers only, then we could make p(x) a true proposition by substituting 5 in for x. Any other integer would yield a truth value of 0. Non-integers would yield undefined values because they are not allowed as inputs. So, p(3.14159265) is undefined.
However, if we restrict allowed inputs to be any real number, then p(3.14159265) is no longer undefined, but would instead be equal to 0.
We could do something crazy and restrict our inputs to names of U.S. presidents. Perhaps we could do this by associating to each president the maximum number of their presidency (we use the maximum number to account for Grover Cleveland’s presidency, where he was the 22nd and 24th president, so Grover Cleveland would be associated with number 24.)
Doing this, we have
| George Washington: | 1 |
| John Adams: | 2 |
| Thomas Jefferson: | 3 |
| James Madison: | 4 |
| James Monroe: | 5 |
| … |
Here, we would have p(George Washington) = 0, whereas p(James Monroe) = 1. Interestingly, since we restricted our inputs to names of U.S. presidents only, that would mean that p(5) would be undefined since no U.S. president was named 5!
The previous examples have shown that restricting the allowable inputs into a propositional function can greatly affect the truth values yielded. The collection of allowable values has a special name, and knowing what this collection consists of is vitally important.
For a given propositional function p(x), the collection of values that are allowed to be substituted in for x is called the universe of discourse, or just universe for short.
Typically, the universe is denoted with 𝒰, but of course other symbols may be used.
Consider the propositional function
r(x): “x has a right angle.”
For r(x), let the universe of discourse 𝒰 be the collection of all planar polygons.
Since the number 2 is not a planar polygon, we would have that the number 2 is not in 𝒰. Therefore r(2) is undefined.
Suppose s1 represents a square with side length 1. s1 is a planar polygon, so s1 is in 𝒰. This means that
r(s1) = 0 or r(s1) = 1.
Since every square has a right angle, we have that r(s1) = 1.
Suppose s2 represents an equilateral triangle with side length 1. s2 is a planar polygon, so either
r(s2) = 0 or r(s2) = 1.
Since no equilateral triangle has a right angle, we would have that r(s2) = 0.
As demonstrated in Example 1.7.3, a propositional function can have many variables. We would need to specify the universe of discourse that all variables have to adhere to.
Consider the propositional function
e(x, y): “x + y is an even integer.”
Let the universe of discourse 𝒰 for x and y be integers.This means that both x and y must be integers.
We would have e(2, 4) = 1, e(3, 7) = 1, e(1, 2) = 0, and e(4, 13) = 0.
e(2, 2.3), e(2.18, 3.14), e (4.411, 10) would all be undefined because 2.3, 2.18, 3.14, and 4.411 are not integers.
e(2, Monday) would also be undefined because Monday is not an integer. Similarly, e(Red, Cactus) would also be undefined.
In order for e(x, y) to yield either 0 or 1, then x needs to be an integer, and y needs to be an integer.
It’s possible to specify a separate universe for every variable in the propositional function.
Consider the propositional function
q(x, y): “x ÷ y is larger than 5.2.”
Let the universe for x, denoted 𝒰x, be all real numbers. Let the universe for y, denoted 𝒰y, be all real numbers except 0.
Here, q(2.2, 0.0001) = 1, q(10, 2) = 0, q(0.52, 0.01) = 1, and q(0.52, 0.1) = 0.
q(1, 0) would be undefined because 0 is not in 𝒰y.
q(Monday, 1) would be undefined because Monday is not in 𝒰x.
q(Friday, 0) would be undefined because Friday is not in 𝒰x, and because 0 is not in 𝒰y.
Consider the propositional function
z(a, b, c): “The band a recorded the song b for album c.”
Here, the universe for a, denoted A, is all bands. Let the universe for b, denoted B, be all song names. Finally, let the universe for c, denoted C, be all musical albums.
We have the following results:
| z(AC/DC, There’s Gonna be Some Rockin’, Dirty Deeds Done Dirt Cheap) | = | 1 |
| z(Fleetwood Mac, Everywhere, Tango in the Night) | = | 1 |
| z(ZZ Top, Sharp Dressed Man, Tres Hombres) | = | 0 |
| z(Metallica, Fuel, Load) | = | 0 |
All of these examples were defined, and so yielded truth values of either 0 or 1, because “AC/DC”, “Fleetwood Mac”, “ZZ Top”, and “Metallica” are all in A.
Similarly, “There’s Gonna be Some Rockin'”, “Everywhere”, “Sharp Dressed Man”, and “Fuel” would all be in B.
Finally, “Dirty Deeds Done Dirt Cheap”, “Tango in the Night”, “Tres Hombres”, and “Load” are all in universe C.
Of course it’s possible that some of the variables in a propositional function can share a universe of discourse, while other variables can have some other universe.
Consider the propositional function
q(x, y, z): “(x + y) ÷ z = 1.”
Let the universe for x and y, denoted M, be all integers. Let the universe for z, denoted N, be all real numbers except 0.
we have that q(1, 0, 1) = 1, q(-2, 7, 5) = 1, q(-1, 1, 1) = 0, and q(10, -23, 2) = 0.
q(0.1, 1, 1) is undefined because the supplied value for x (0.1) is not in M.
Similarly, q(23, -3.14, 10) is also not defined because the supplied value for y (-3.14) is not in y’s universe, which is M.
Finally, q(20, -10, 0) is undefined because the supplied value for z (0) is not in z’s universe, which is N.