Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
The Book of
Foundational Mathematics
Arguments and Proof
- The Structure of Basic Arguments
- Rules of Inference
- Using the Rules of Inference
- Logically Equivalent Arguments
- Invalid Arguments
- Universal Specification
- Universal Generalization
- Axioms, Definitions, Theorems, and Proofs
- Proof Technique: Direct Proofs
- Proof Technique: Indirect Proofs
- Proof Technique: Contradiction
- Mistakes in Proofs
- Proof Technique: Equivalence
Logical Implications
Out of the two kinds of conditional statements we’ve looked at, those being → and ↔, we’ve taken a close look at ↔. Now, we take a closer look at → to see what we can do with that.
A Simple Equivalency
Let’s take a look at the implication p → q. What is this proposition saying? Before taking a look at a truth table, let’s think about it from a linguistic perspective. The English translation of this statement is “if p, then q.” Consider the following example.
Example 1.6.1
Suppose we have that p → q where
| p: | “Alyssa studies for her Chemistry exam” |
| q: | “Alyssa gets an A on her Chemistry exam” |
What can we deduce if we know ¬p is true (meaning p is false?) In this scenario, Alyssa does not study for her Chemistry exam. Does this mean she does not get an A on her Chemistry exam?
Not necessarily. Remember, all we know is that if she does study, she’ll get an A. We were not told ¬p → ¬q. Perhaps the exam is really easy and Alyssa does not feel the need to study. Perhaps the exam is difficult, but Alyssa is really good at guessing and eliminating wrong answers, or perhaps she is comfortable enough with the material to be able to work out correct answers with a little bit of thought. On the other hand, the exam could be extremely difficult for Alyssa, so maybe she does not get an A.
All we can figure out is that she does not study. We can not figure out if we have q or ¬q, all we know in this scenario is that we have ¬p.
What if we know we have p instead of ¬p? Well, since we know that if Alyssa studies, she will get an A on her Chemistry exam. Thus knowing that p happened, we also know that q happened. Note that since we’re asserting that p → q is true, we can’t have p → ¬q.
Our conclusion hinges on the truth value of p. If we know ¬p happened, we don’t have any additional conclusions. However if p happened, then we know q happens as well. There are 3 possible outcomes from the statement p → q:
¬p
q
¬p ∧ q
This corresponds to the logical statement ¬p ∨ q.
Figure 1.6.1: When we construct the truth table for the expression
(p → q) ↔ (¬p ∨ q)
using Maple, we see that it has all 1s in the last column, meaning this statement is a tautology.
Example 1.6.1 seems to suggest that the statements p → q and ¬p ∨ q are logically equivalent. In other words, if we construct a truth table for the expression
(p → q) ↔ (¬p ∨ q),
then we’ll see an entire column of 1s. As demonstrated in Figure 1.6.1, that is exactly what we see. This means we have the following equivalency:
(p → q) ⟺ (¬p ∨ q).
This fact demands extra emphasis:
A Logical Equivalence for p → q
We have the following logical equivalency:
(p → q) ⟺ (¬p ∨ q)
Without having this logical equivalence in mind, negating implications can be quite tricky. With this fact in mind however, it becomes rather trivial:
| ¬(p → q) | Law of Logic Used | |
| ⟺ | ¬(¬p ∨ q) | (p → q) ⇔ (¬p ∨ q) |
| ⟺ | ¬¬p ∧ ¬q | DeMorgan’s Law |
| ⟺ | p ∧ ¬q | Law of Double Negation |
So the negation of (p → q) is the statement (p ∧ ¬q), which seems reasonable. Remember that the implication is false when p = 1 and q = 0.
Now’s a good time to emphasize the importance of using parenthesis to manipulate the order of operations in a logical statement.
Figure 1.6.2: In (a), we see the truth table for ¬p → q, which is the same expression as (¬p → q). In (b), we have the truth table for ¬(p → q). Seeing these two table side-by-side confirms the differences that exist between the expressions (¬p → q) and ¬(p → q).
It’s important that, when transcribing logical expressions, we put parenthesis around whatever statements we want to negate. Just like with arithmetic, parenthesis are used to change the order of operations in logical expressions, and any change in the order of operations can yield substantial changes in the outcome.
Typically, an expression such as
¬p → q
is shorthand for the statement
(¬p) → q.
In other words, the negation operation ¬ is the most strongly binding operation in an expression. Any doubts can always be alleviated by using parenthesis.
Relating Implications to Biconditionals
One more observation we can make about the biconditional statement a ↔ b is that it would seem that this would be equivalent to both (a → b) and (b → a).
Example 1.6.2
Suppose we have the following statements concerning certain kinds of triangles:
| a: | “△ABC is equilateral” |
| b: | “△ABC is equiangular” |
From Geometry, we know that a → b. That is, as soon as we know △ABC is equilateral, we also know that △ABC is equiangular (in this case, we know that all angles are 60°.)
It works the other way as well. As soon as we know △ABC is equiangular, we also know that △ABC is equilateral.
In this case, statements a and b come hand in hand. We can’t have one without the other. Hence, we write
a ↔ b.
The same holds true for the negated statements as well. We have both
¬a → ¬b
¬b → ¬a.
That is once we know △ABC is not equilateral, we also know it is not equiangular, and vice-versa.
Figure 1.6.3: Here we see the truth table for the logical expression
((a → b) ∧ (b → a)) ↔ (a ↔ b).
Again, notice that this statement is a tautology.
We formalize the relationship between ↔ and → in the figures to the left and below.
Figure 1.6.4: In (a), we see the truth table for (a → b) ∧ (b → a). In (b), we see the truth table for a ↔ b. Finally in (c), we see the truth table for (a ∧ b) ∨ (¬a ∧ ¬b). Notice that in the last column, they all have 0s in the same rows and 1s in the same rows. Hence, they are all logically equivalent.
Based on Example 1.6.2, we have another important highlight:
Logical Equivalence between ↔ and →
| a ↔ b | |
| ⟺ | (a → b) ∧ (b → a) |
| ⟺ | (a ∧ b) ∨ (¬a ∧ ¬b) |
Tautologically True Implications
Example 1.6.3
Consider the statement
a ∧ (a → b).
where we have
| a: | “Smith wields a red lightsaber” |
| b: | “Smith is a Sith” |
A direct translation of the statement above would be
“Smith wields a red lightsaber, and if Smith wields a red lightsaber, then Smith is a Sith.”
Part of the statement says that if Smith wields a red lightsaber, then Smith is a Sith. Notice that this statement alone does not say that Smith is a Sith. What we do know is that Smith wields a red lightsaber. Since we know he wields a red lightsaber, we can use the implication to deduce that Smith is a Sith.
Hence, the conclusion we would draw from both of these statements is b, which represents the statement “Smith is a Sith.”
What if we already knew that Smith was a Sith? In other words, we already know b. Does that give us enough information to conclude a ∧ (a → b)? If a = 0 and b = 1, then
b → (a ∧ (a → b))
would be false. In other words, we have
(a ∧ (a → b)) → b,
but not
b → (a ∧ (a → b)).
As always, we should look at a truth table to get a better idea of what’s going on.
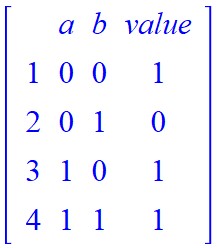
Figure 1.6.5: In (a), we see a truth table for the expression (a ∧ (a → b)) → b. In (b), we see the truth table for the expression (a ∧ (a → b)) ↔ b.
In part (a) of Figure 1.6.5, the truth table for the expression (a ∧ (a → b)) → b reveals all 1s in the last column. Thus the logical implication (a ∧ (a → b)) → b is a tautology. However, we see the truth table for the biconditional (a ∧ (a → b)) ↔ b in part (b) of Figure 1.6.5. There is a single 0 in the last column, so while the biconditional is satisfiable, it is not a tautology.
There is a special name for these kinds of implications.
Logically Implies
Suppose a and b are any arbitrary statements (primitive or compound) such that the implication
a → b
is always true, or in other words, a tautology. We say that a logically implies b, and we write
a ⟹ b.
If a → b is not a tautology, we write
a ⇏ b.
Based on the proposition given above where we saw that
(a ∧ (a → b)) → b
was a tautology, we could use our new notation and write
(a ∧ (a → b)) ⟹ b.
Related Implications
There are some simple ways we can change around implications. The way we make this changes will impact how any new implications we form are related to our original starting implication. The first two modifications are relatively straight-forward.
Converse, Inverse
Consider the implication a → b, which will act as our starting point. Here, a and b could be primitive or compound statements themselves.
The converse of a → b is the implication
b → a.
The inverse of a → b is the implication
¬a → ¬b.
Basically, the converse is obtained by swapping the two statements on either side of the arrow →. The inverse is obtained by negating both statements on either side of the arrow →.
Of course, we get apply both transformations at the same time. There is of course a special name for that transformation as well.
Contrapositive
Consider the implication a → b, where a and b could be primitive or compound statements themselves.
The contrapositive of a → b is the implication
¬b → ¬a.
As always, an example where we use the English language will illuminate some key aspects of these kinds of propositions.
Example 1.6.4
Consider the implication t → s where we have
| t: | “Taylor Swift releases a new album” |
| s: | “The album will be successful” |
The converse could be translated to
“If an album is successful, then it was released by Taylor Swift.”
The inverse can be translated to
“If Taylor Swift does not release an album, then that album will not be successful.”
Finally, the converse would basically read
“If an album is not successful, then it was not released by Taylor Swift.”
Based on Taylor Swift’s past success, the implication t → s certainly seems like a reasonable statement that is always true. However, notice that the converse does not always appear to be true. Indeed, many successful albums have been released by artists other than Taylor Swift. AC/DC’s album “Back in Black” was a wildly successful album, and Michael Jackson’s “Thriller” is perhaps the most sold album of all time.
The inverse does not appear to be true all the time either (assuming t → s is always true of course.) Again, other artists release successful albums all the time.
The contrapositive is more interesting. Any non-successful album couldn’t have been released by Taylor Swift because if it was released by Taylor Swift, then it would have been successful. Taylor Swift does not make unsuccessful albums, so it would seem that the contrapositive is always true. Furthermore, if we assume that t → s is false (unfathomable, but for the sake of the argument, let’s imagine that is the case,) then the contrapositive would also be false as well.
We have the following truth table relating an implication to its converse, inverse, and contrapositive.
| p | q | p → q | q → p | ¬p → ¬q | ¬q → ¬p |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Notice that the values in the p → q column exactly match the values in the contrapositive column:
| p | q | p → q | q → p | ¬p → ¬q | ¬q → ¬p |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
This tells us that an implication is always logically equivalent to its contrapositive; in other words,
p → q ⟺ ¬q → ¬p.
Additionally, the values in the converse column exactly match those of the inverse column:
| p | q | p → q | q → p | ¬p → ¬q | ¬q → ¬p |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
This tells us that an implication’s converse is logically equivalent to its inverse, meaning
q → p ⟺ ¬p → ¬q.
Yet again, this is worth highlighting:
Equivalence of the Converse, Inverse, and Contrapositive
p → q ⟺ ¬q → ¬p
q → p ⟺ ¬p → ¬q
Since we figured out that an implication is logically equivalent to its contrapositive, we could have deduced that the converse and inverse are logically equivalent by noticing that the inverse is the contrapositive of the converse (and vice-versa.)