Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
The Book of
Foundational Mathematics
Arguments and Proof
- The Structure of Basic Arguments
- Rules of Inference
- Using the Rules of Inference
- Logically Equivalent Arguments
- Invalid Arguments
- Universal Specification
- Universal Generalization
- Axioms, Definitions, Theorems, and Proofs
- Proof Technique: Direct Proofs
- Proof Technique: Indirect Proofs
- Proof Technique: Contradiction
- Mistakes in Proofs
- Proof Technique: Equivalence
A Set of Operations on Sets
We’ve discussed how to construct new sets by simply taking some of the elements from one set, and putting them into a new set. While subsets are vitally important not only in Set Theory and throughout all of mathematics, subsets are formed by only considering one set at a time.
We can construct a wide variety of sets by considering two or more sets at a time. In this section, we learn what kinds of sets we can construct by considering more than one set at a time.
Complement
Before we talk about more than one set a time, let’s talk about one more operation that only relies on one set. Technically, it does require two sets because this particular operation requires knowing what universe is being considered.
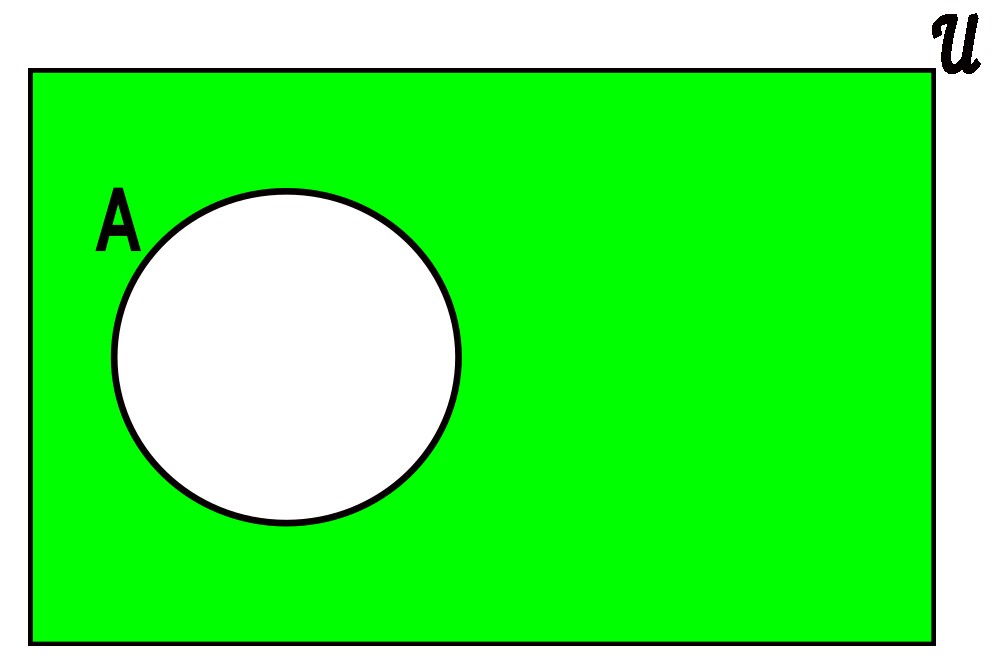
Figure 3.4.1: The complement of a set A, denoted AC, is the set of all elements within 𝒰 that are not within A.
Complement
Consider a set A consisting of elements taken from some universal set, denoted 𝒰.
The complement of A, often denoted AC or A, is the set of all elements in 𝒰 that are not in A.
In other words, we have that
AC = A = { x ∈ 𝒰 | x ∉ A }.
The idea of set complement is really simple: we take all elements within 𝒰 that are not in A, and put all of those elements in a new set we usually call either AC or A, though occasionally other names are used.
Example 3.4.1
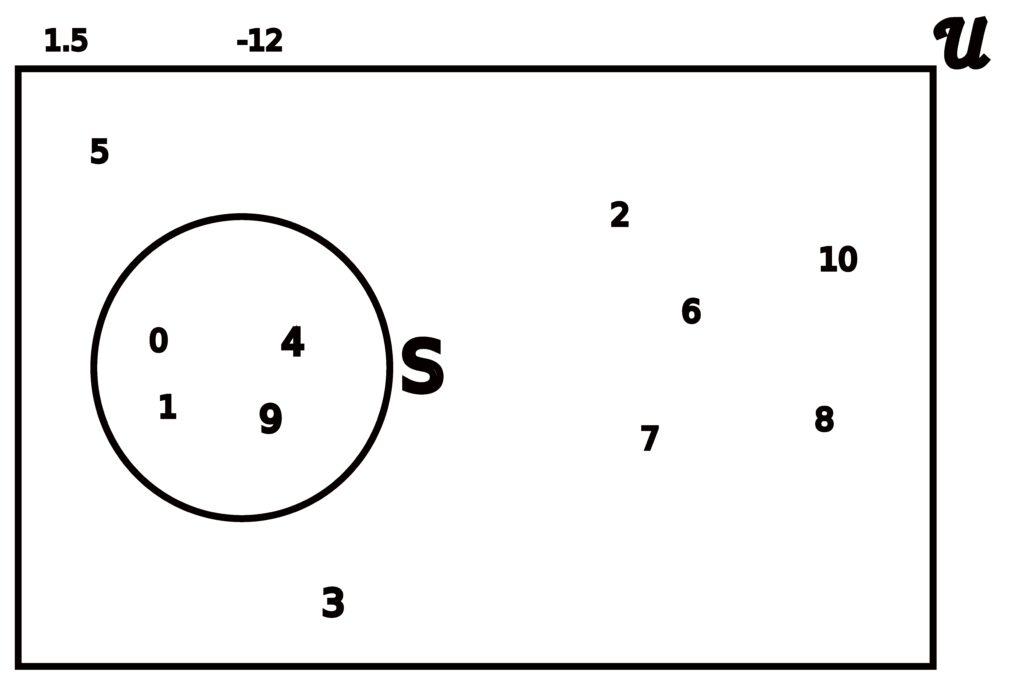
Consider a universal set 𝒰 consisting of all the whole numbers from 0 to 10 inclusive, meaning
𝒰 = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }.
Now consider the set S of all perfect squares contained within 𝒰, meaning we have
S = { 0, 1, 4, 9 }.
We then get that
SC = { 2, 3, 5, 6, 7, 8, 10 }.
Of course, the essential property we care about when it comes to sets is whether a specific element is a member of that set or not. How do we tell that an element x is in AC or not? Based on the definition of complement, we see that the following logical equivalency is used to test if x is in A’s complement:
(x ∈ AC) ⟺ (x ∈ 𝒰 ∧ x ∉ A)..
Example 3.4.2
Reconsider the sets mentioned in Example 3.4.1:
| 𝒰 | = | { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 } |
| S | = | { 0, 1, 4, 9 } |
Is 5 in S or in SC? Of course 5 ∈ 𝒰, so it will either be in S or SC. Of course, S was defined to be the set of all elements from 𝒰 that are perfect squares. Since 5 ∈ 𝒰 and 5 is not a perfect square, we know that
5 ∈ SC.
Now consider the number 9. Because 9 ∈ 𝒰 and 81 is a perfect square (9 = 32), we have that
9 ∉ SC.
What about a number like 1.5? Remember that 𝒰 only consists of whole numbers between 0 and 10. Since 1.5 is not a whole number, we have that 1.5 ∉ 𝒰, and as such we have that
| 1.5 ∉ S | 1.5 ∉ SC |
Similarly to the number 1.5, because -12 ∉ 𝒰,, we also have that
| -12 ∉ S | -12 ∉ SC |
Union
Now that we’ve talked about what’s outside a set, we can start to consider what happens when we combine two sets into one.
The first thing we can do is take all elements from two different sets, and simply mash them all up into one set.
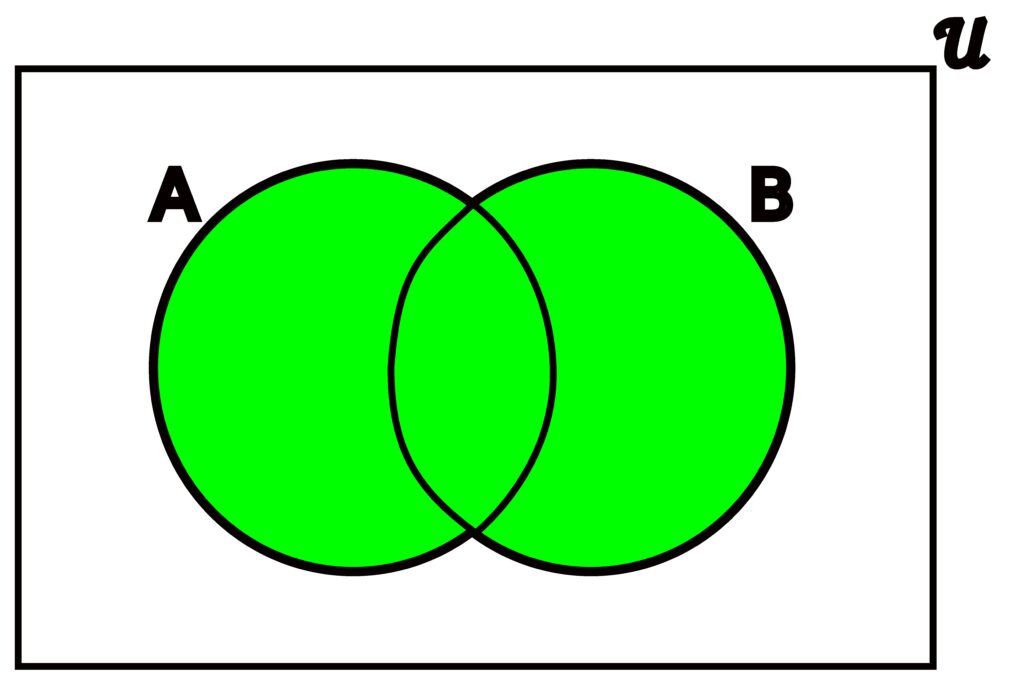
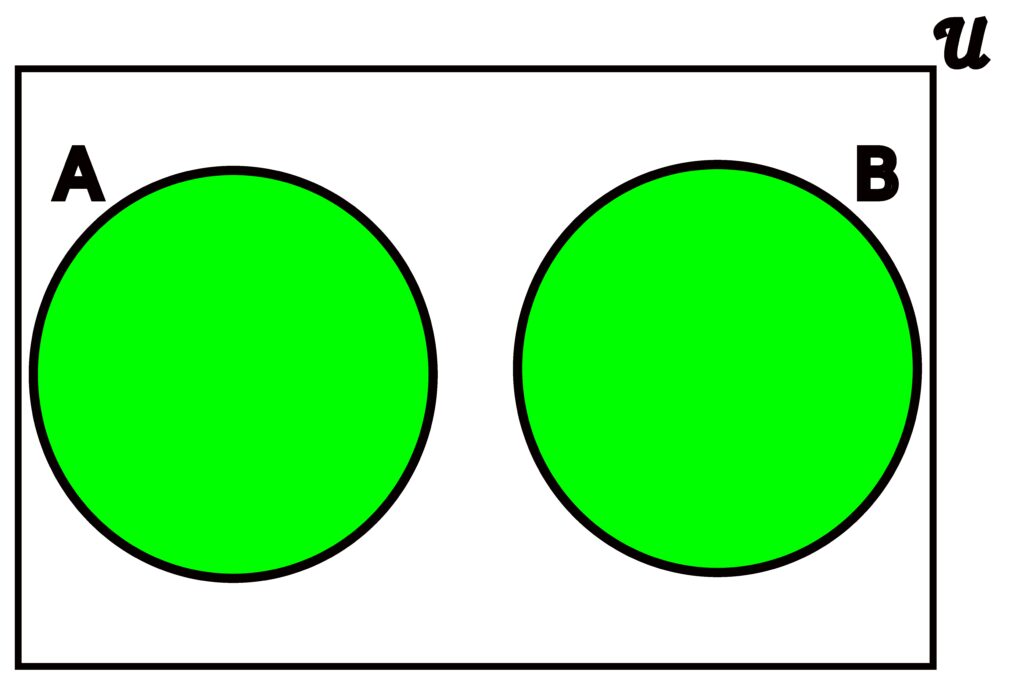
Figure 3.4.2: The union of two sets is simply the set containing any element contained in either set. Any part of any set will be shaded green to indicate it is in the union. In (a), A and B share some overlap, but that overlap is still included. In (b), A and B do not have any common elements and are totally separate, but are still entirely shaded green.
Union
Consider two sets A and B composed of elements from some universal set 𝒰.
The union of sets A and B, denoted A ∪ B, is the set
A ∪ B = { x ∈ 𝒰 | x ∈ A ∨ x ∈ B }.
As long as an element is in A or B, or even both A and B, it will be included in the union of A and B.
Example 3.4.3
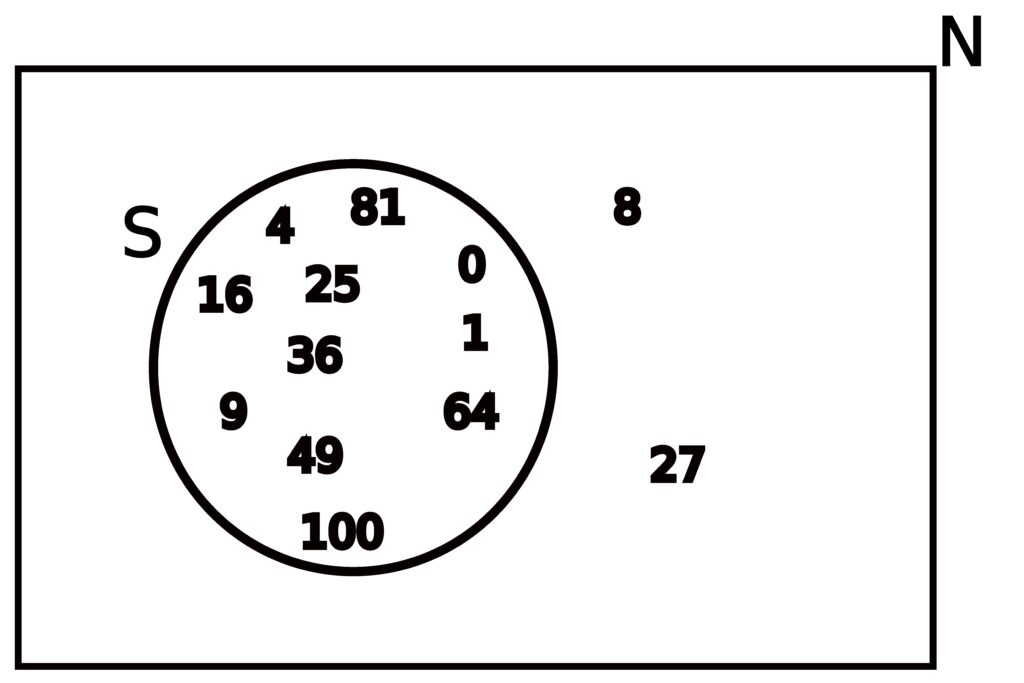
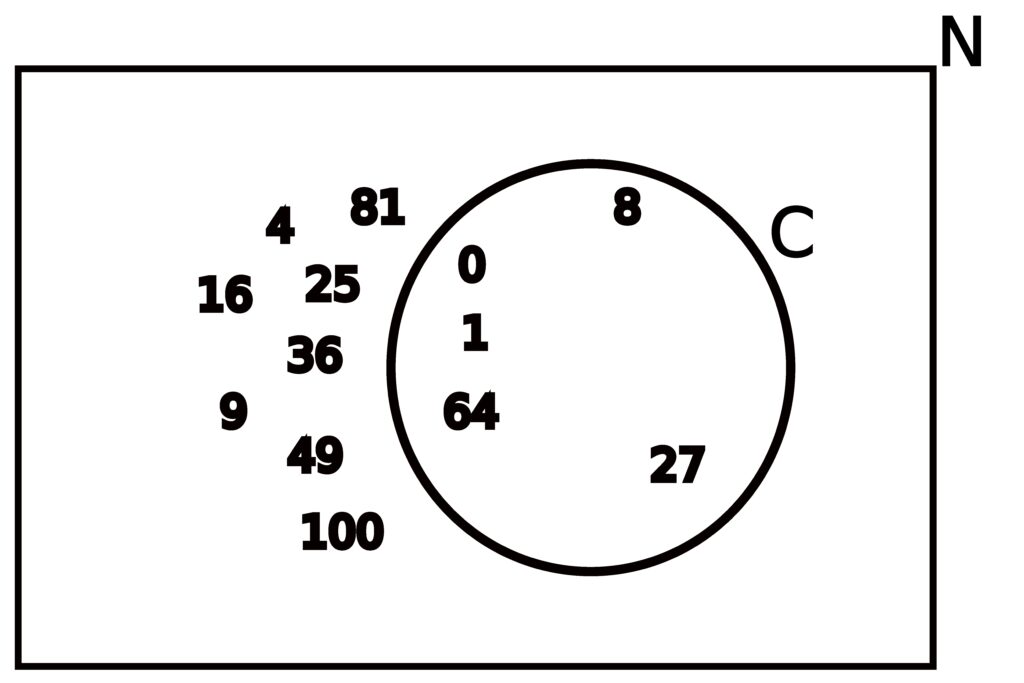
Lets consider some universal set, which we’ll refer to as N, consisting of the whole numbers from 0 to 100 inclusive, meaning
N = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 98, 99, 100 }.
Now consider the following sets:
| S | = | { 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 } |
| C | = | { 0, 1, 8, 27, 64 } |
For clarity, the set S is the set of all perfect squares that are contained in N, and C is the set of all perfect cubes contained within N.
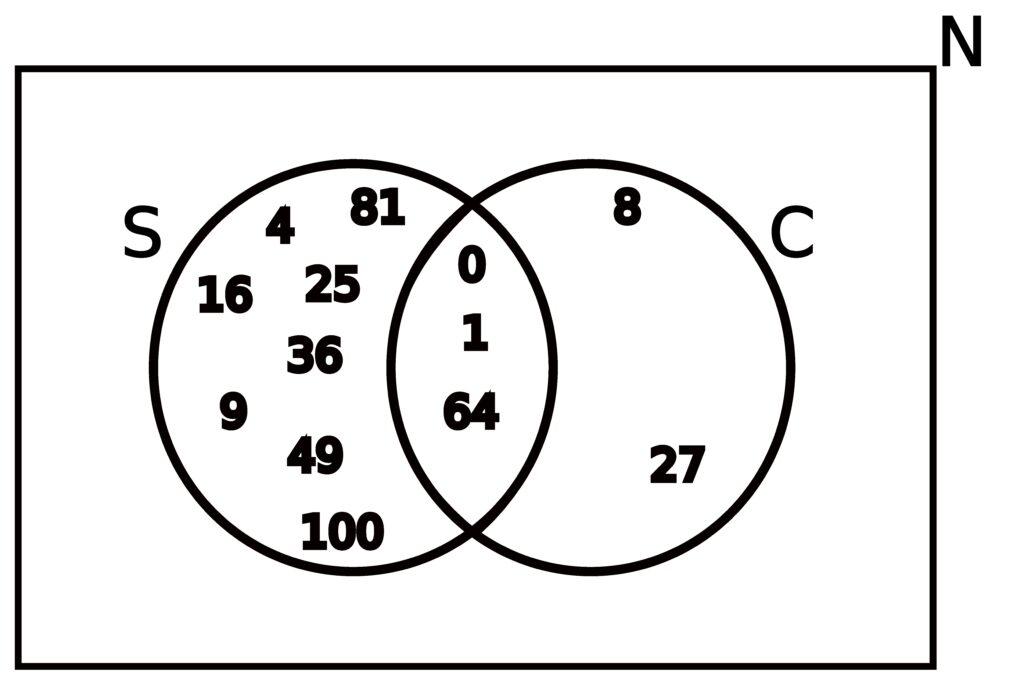
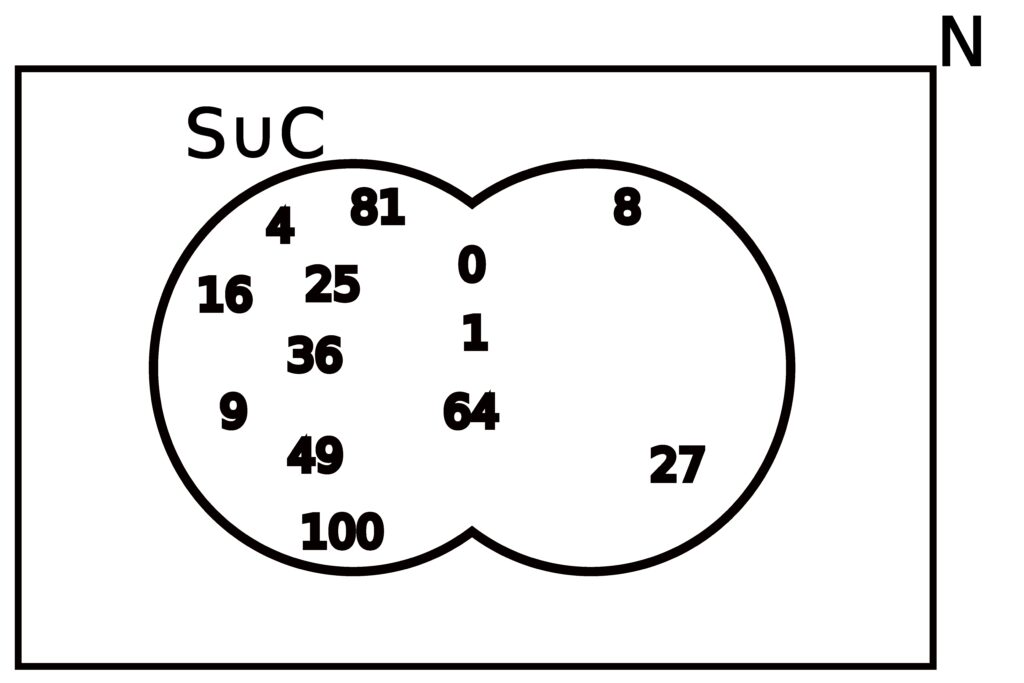
The union of sets S and C is simply the set containing all the elements from S or C, or even both. As such, we get that
S ∪ C = { 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 0, 1, 8, 27, 64 }.
Even though in some sense, the above set is correct, remember that when dealing with a set, order and repetition are irrelevant. As such, we can simplify how the set is written in the following way:
| S ∪ C | = | { 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 0, 1, 8, 27, 64 } |
| = | { 0, 0, 1, 1, 4, 8, 9, 16, 25, 27, 36, 49, 64, 64, 81, 100 } | |
| = | { 0, 1, 4, 8, 9, 16, 25, 27, 36, 49, 64, 81, 100 } |
In simplifying how we wrote the set referred to by S ∪ C, we started by ordering all the numbers (because order is irrelevant), which makes it easy to see any duplicate entries. After seeing where the duplicates were, we were able to eliminate the duplicates (because repetition is irrelevant.)
Example 3.4.4
Reconsider the set
N = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 98, 99, 100 }
from Example 3.4.3.
Now, consider the following two sets:
| X | = | { x ∈ N | x is an odd perfect square } |
| { 1, 9, 25, 49, 81 } |
| Y | = | { y ∈ N | y is an even perfect cube } |
| = | { 0, 8, 64 } |
The union of X and Y is thus
| X ∪ Y | = | { 1, 9, 25, 49, 81, 0, 8, 64 } |
| = | { 0, 1, 8, 9, 25, 49, 64, 81 } |
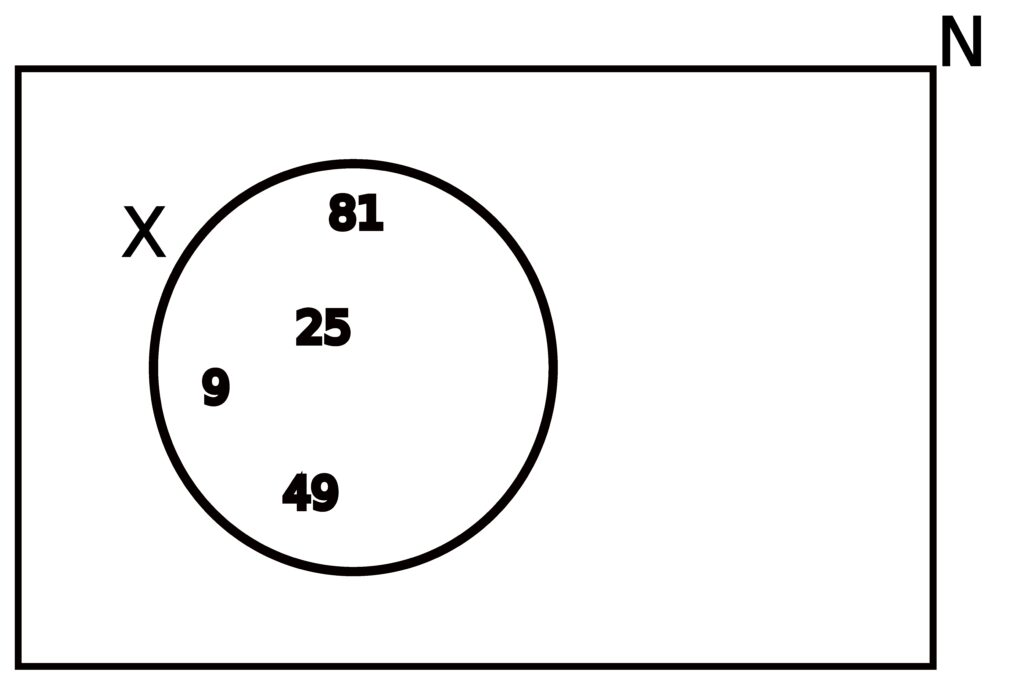
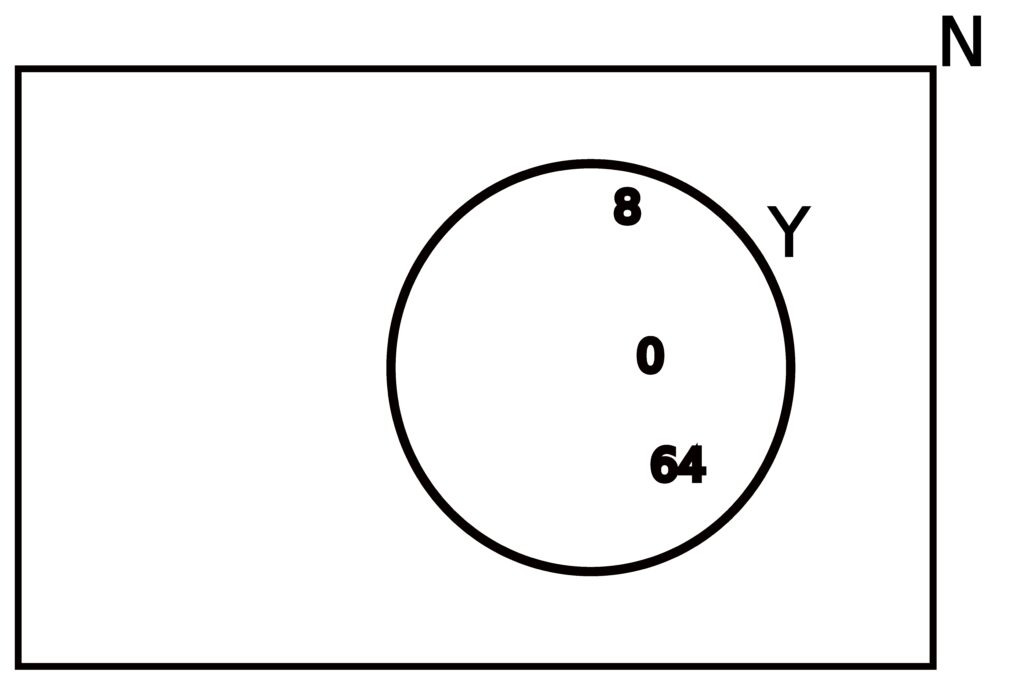
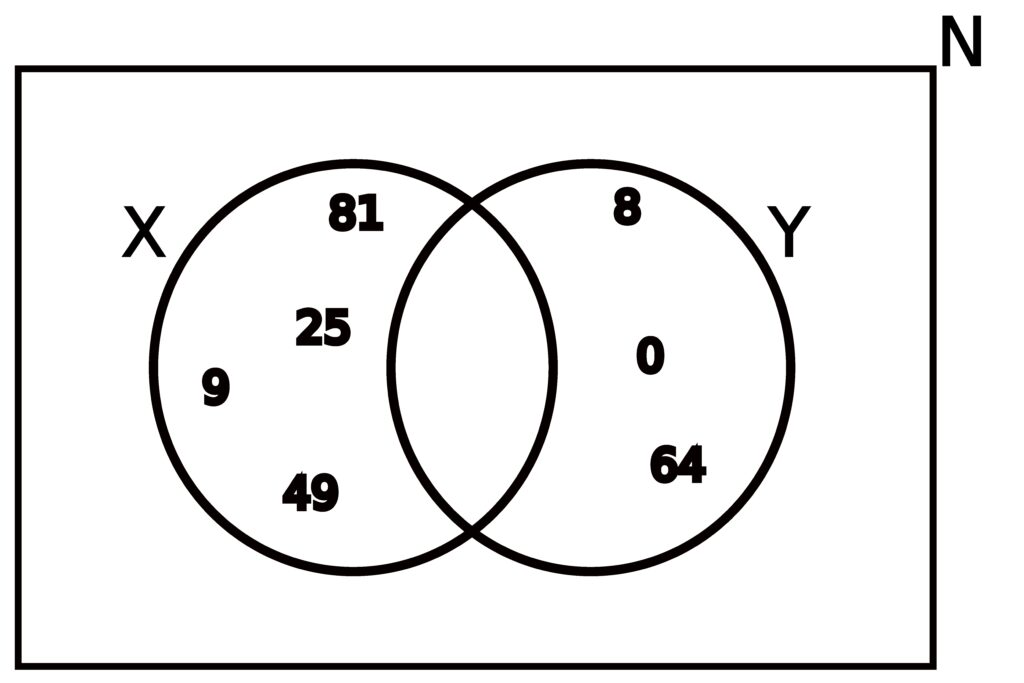
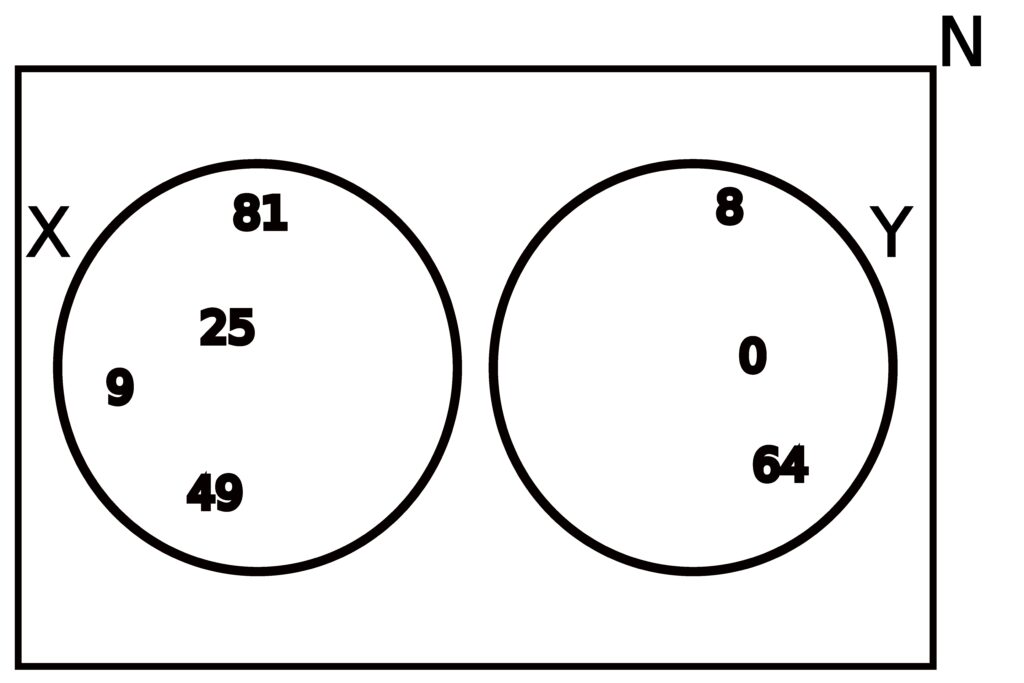
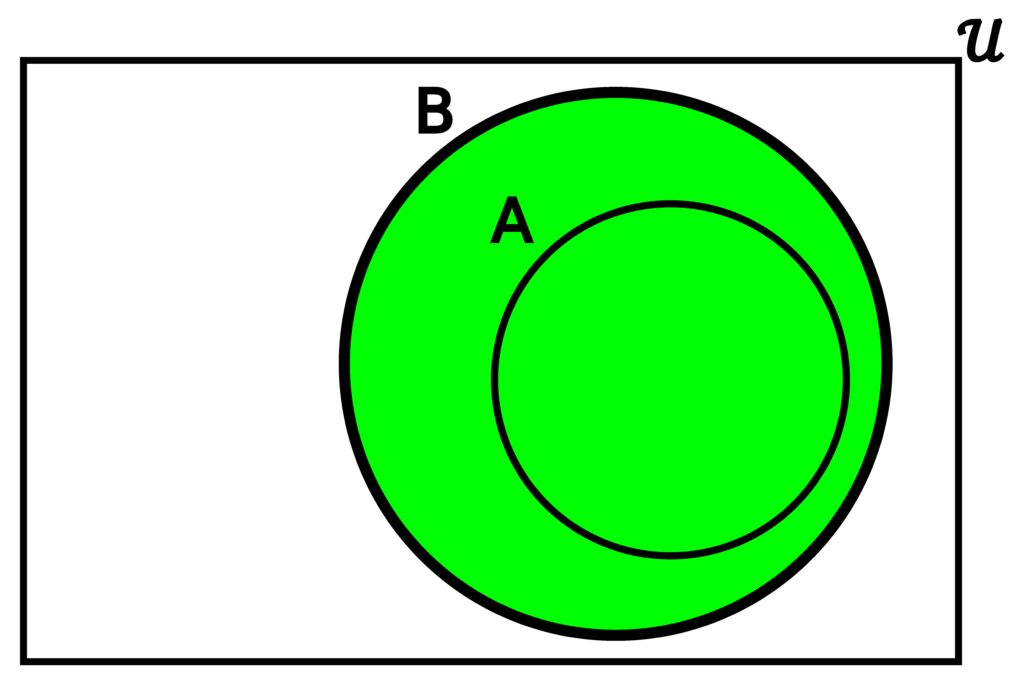
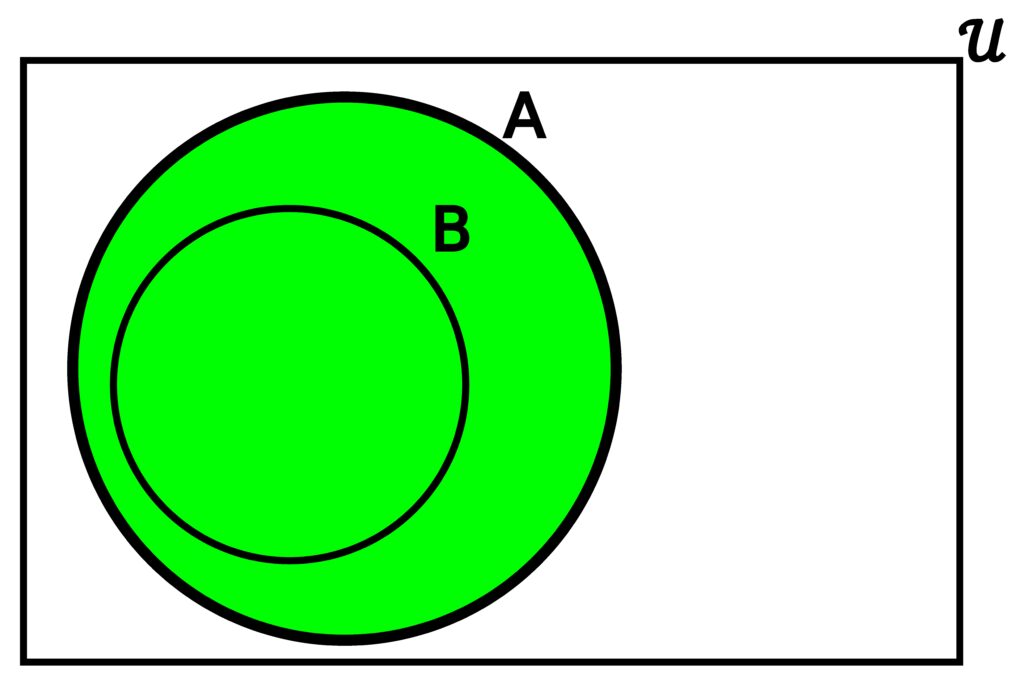
Figure 3.4.3: When one of A or B is a subset of the other, the union of the two will simply be whichever is not the subset. In (a), we see that since A is contained entirely in B, then A ∪ B = B. Likewise, in (b), we see that since B is contained entirely within A, we have that A ∪ B = A.
One situation not yet considered is when one set is entirely contained within another. Because a union consists of elements contained in either set, this means that the union will actually just be whichever set contains the other one.
Example 3.4.5
Consider the sets
| N | = | { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 98, 99, 100 } |
| S | = | { 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 } |
| Q | = | { 0, 1, 16, 81 } |
where N is the universal set under consideration. Here, S represents perfect squares within N, and Q is the set of all perfect fourth powers contained in N. Because all elements in Q are also in S, there is no difference between
S ∪ Q = { 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 }
and S.
Intersection
Another kind of set we can compose from two other sets is to take elements that are in both sets. Here, we are not taking elements that are present in either set; instead, we demand that the elements are present in both sets.
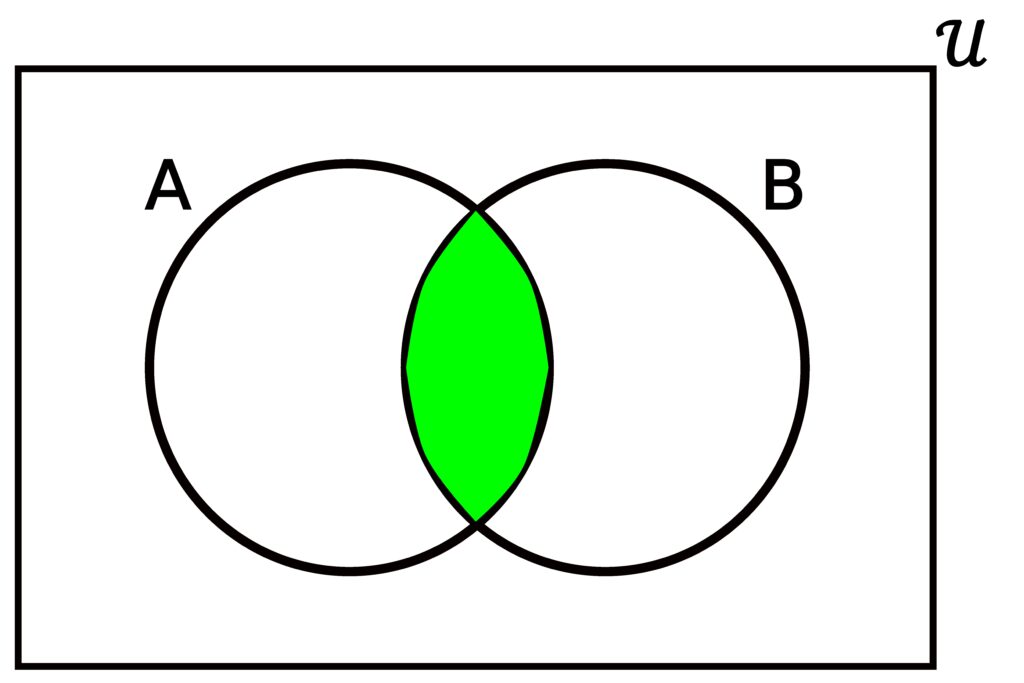
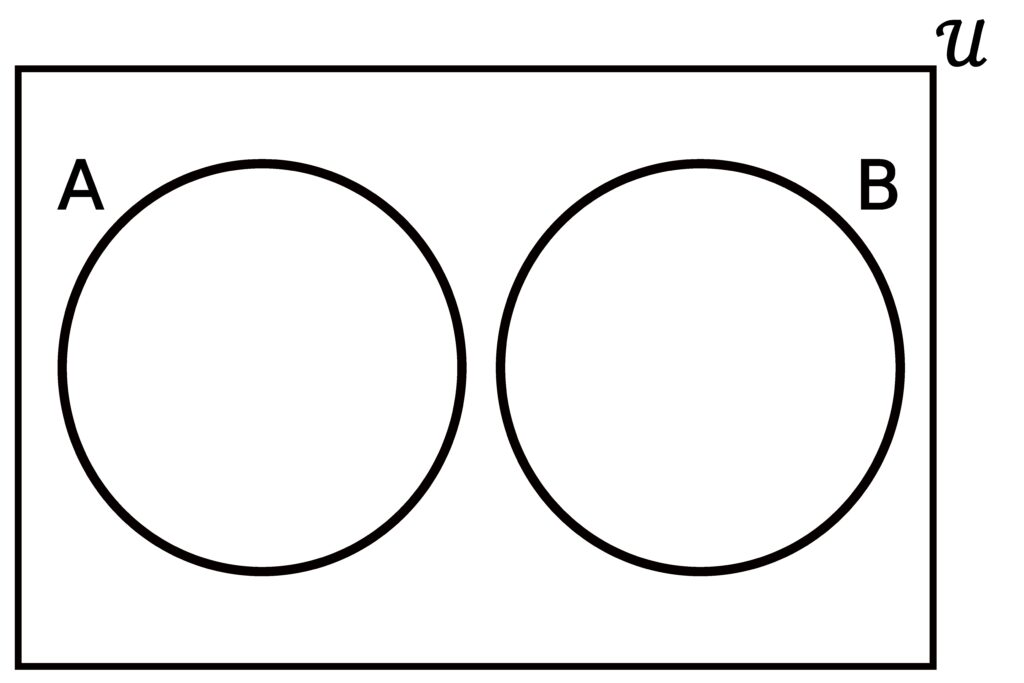
Figure 3.4.4: The intersection of two sets is the set containing all elements that are in both sets. The only part of the graphic representation above that can be colored green is the overlap between the two circles, because it is only the overlapping region that represents elements contained in both sets.. In (a), A and B share some overlap, and so the overlapping region is colored green. No other part can be colored green because no other part is shared by both A and B.. In (b), A and B do not have any common elements and are totally separate, and so no part of the picture can be colored green..
Intersection
Consider two sets A and B composed of elements from some universal set 𝒰.
The intersection of sets A and B, denoted A ∩ B, is the set
A ∩ B = { x ∈ 𝒰 | x ∈ A ∧ x ∈ B }.
Just like with the union of two sets, we would like to determine if an element x is contained within the intersection of two sets. As such, there is a logical equivalency we can use to determine if element x is contained within A ∩ B:
(x ∈ A ∩ B) ⟺ (x ∈ A ∧ x ∈ B).
Before continuing on, it’s worth pointing out the similarity between the union and intersection symbols with the logical or and and operators respectively:
| ∪ | pairs with | ∨ |
| ∩ | pairs with | ∧ |
Example 3.4.6
Going back to Example 3.4.3, we have the following sets:
| N | = | { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 98, 99, 100 } |
| S | = | { 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 } |
| C | = | { 0, 1, 8, 27, 64 } |
To figure out what elements are in S ∩ C, we simply look for elements that are in both A and B:
S ∩ C = { 0, 1, 64 }.
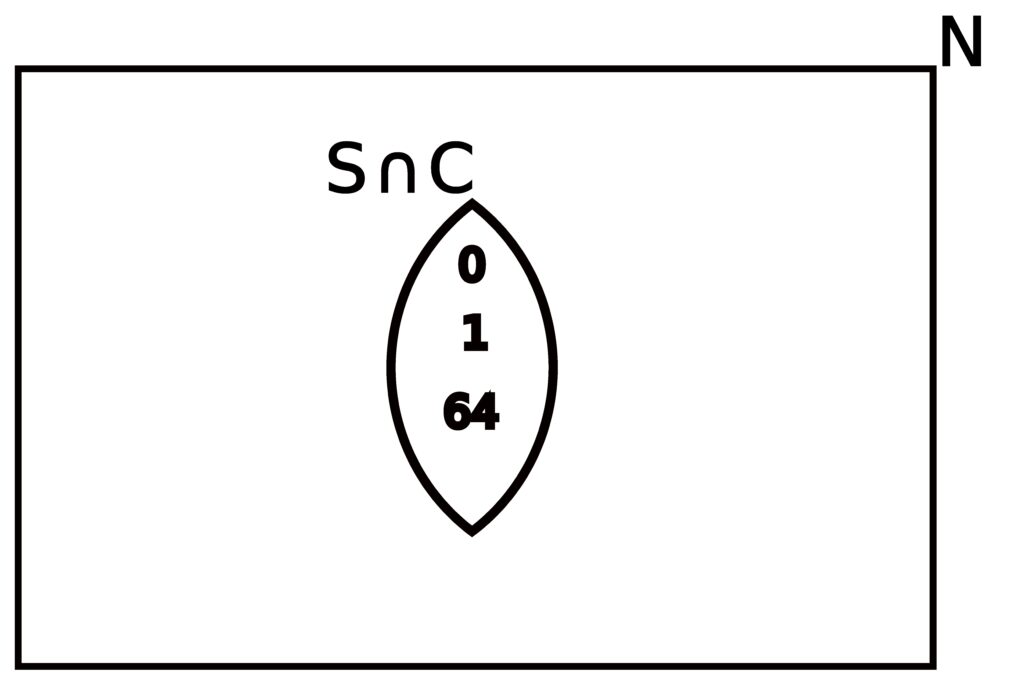
Look again at part (b) of Figure 3.4.3. Notice that when the two sets in question do not overlap, there is nothing shaded green. Of course, this means that the set A ∩ B has nothing in it, or in other words,
A ∩ B = { } = ∅.
This means that the intersection of two sets with nothing in common is simply the empty set.
Example 3.4.7
Reconsider the sets defined in Example 3.4.4.
| N | = | { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 98, 99, 100 } |
| X | = | { 1, 9, 25, 49, 81 } |
| Y | = | { 0, 8, 64 } |
In this case, since X and Y share no elements in common, we have that
X ∩ Y = ∅.
When one of A or B is a subset of the other, the intersection will end up just being whichever set was the subset.
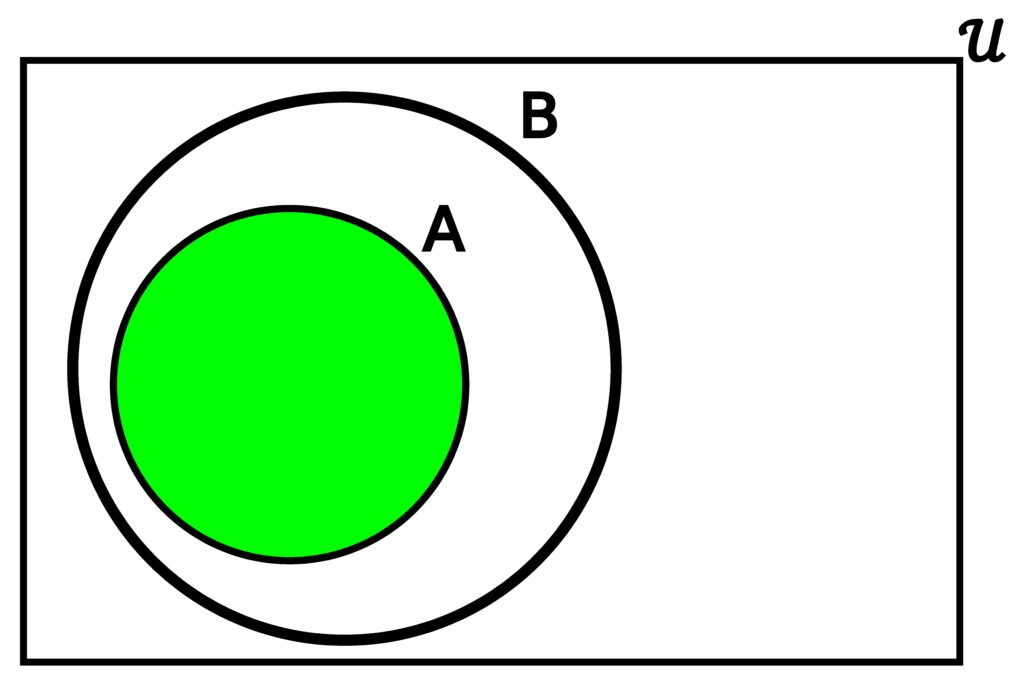
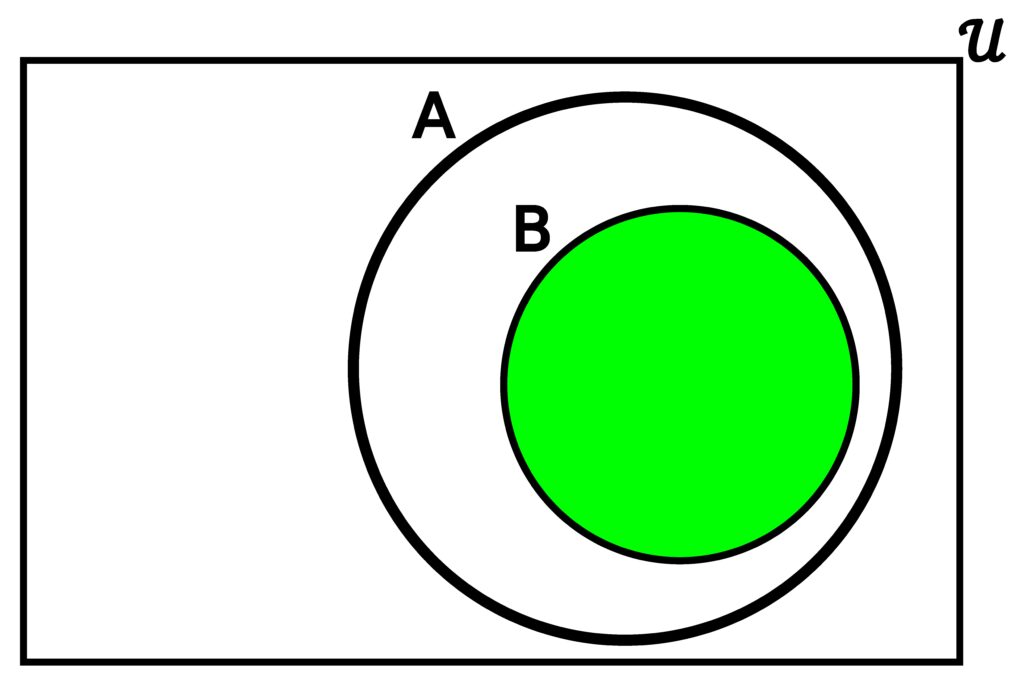
Figure 3.4.5: When either A or B is a subset of the other, then the intersection will be whichever set happens to be the subset. In (a), we see what A ∩ B is when A ⊆ B. In (b), we see what A ∩ B is when B ⊆ A.
Example 3.4.8
Consider the sets
| N | = | { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 98, 99, 100 } |
| S | = | { 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 } |
| Q | = | { 0, 1, 16, 81 } |
We see that
S ∩ Q = { 0, 1, 16, 81 } = Q.
Difference
It’s possible that we may want to exclude certain elements from the universe within any sets we construct. Of course, any given set can contain any element from the universe, whether or not we want it included. One thing we can do to remedy such a situation is to collect all of the elements we want excluded in a special set which we’ll refer to as B for now (which we could call an “exclusion set”.) Then, for some given set we’ll call A, we can make a new set by removing all elements from A that are also in B. This will give us a new set containing all elements from A that we don’t want excluded.
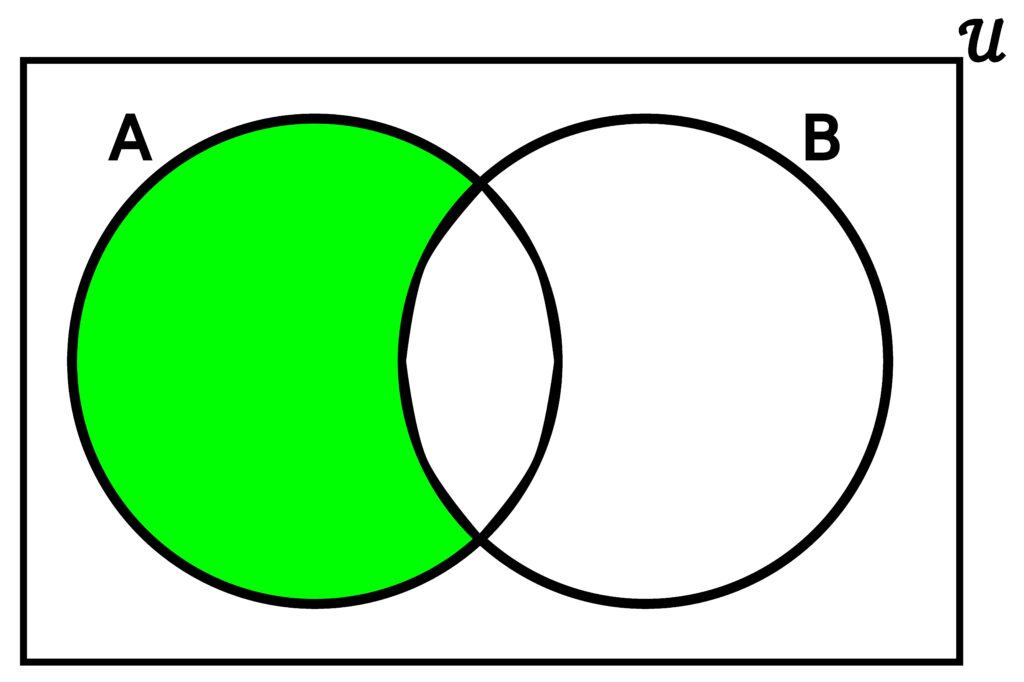
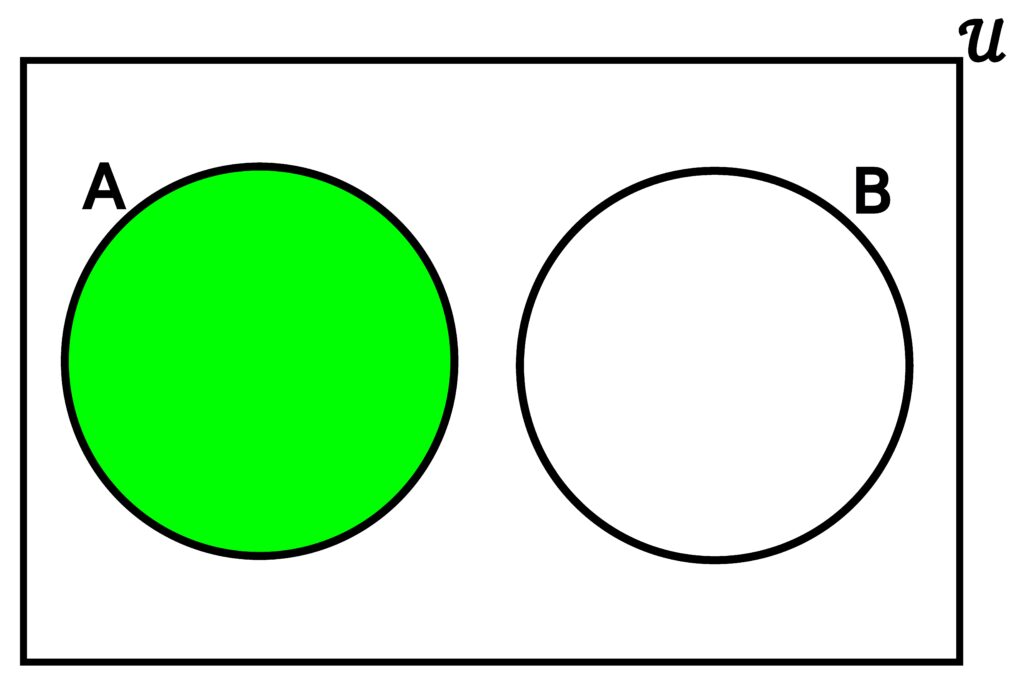
Figure 3.4.6: The difference A – B is simply the set of all elements in A that are not in B. In (a), we see that since there is some overlap between A and B, the overlap must not be colored green because those elements are in B. In (b), we see that since there is no overlap, every element in A can be included in A – B since A doesn’t contain any elements that are also in B.
Difference
Consider two sets A and B containing elements from some universal set 𝒰.
The difference from B to A, which we’ll denote A – B, is the set of all elements in A that are not in B. In other words,
A – B = { x ∈ 𝒰 | x ∈ A ∧ x ∉ B }.
Once again, there is a logical equivalency we can use to determine if a given object is contained in the set A – B:
(x ∈ A – B) ⟺ (x ∈ A ∧ x ∉ B).
Example 3.4.9
Reconsider the following sets:
| N | = | { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 98, 99, 100 } |
| S | = | { 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 } |
| C | = | { 0, 1, 8, 27, 64 } |
where N is the universal set, from which sets S and C share elements.
In order to determine which elements are in S – C, we start with S, and take away any elements that are also in C. What we could do is look at the intersection of S and C:
S ∩ C = { 0, 1, 64 }.
Now, all we have to do is simply copy S, but remove all those elements that are S ∩ C:
S – C = { 4, 9, 16, 25, 36, 49, 81, 100 }.
We can do the same thing to C – S. We simply start with C, and take away elements that are also in S, (remember that all the common elements are in S ∩ C):
C – S = { 8, 27 }.
Care should be taken when one of the sets is a subset of the other one (in other words, when one of the sets is entirely contained within the other one.)
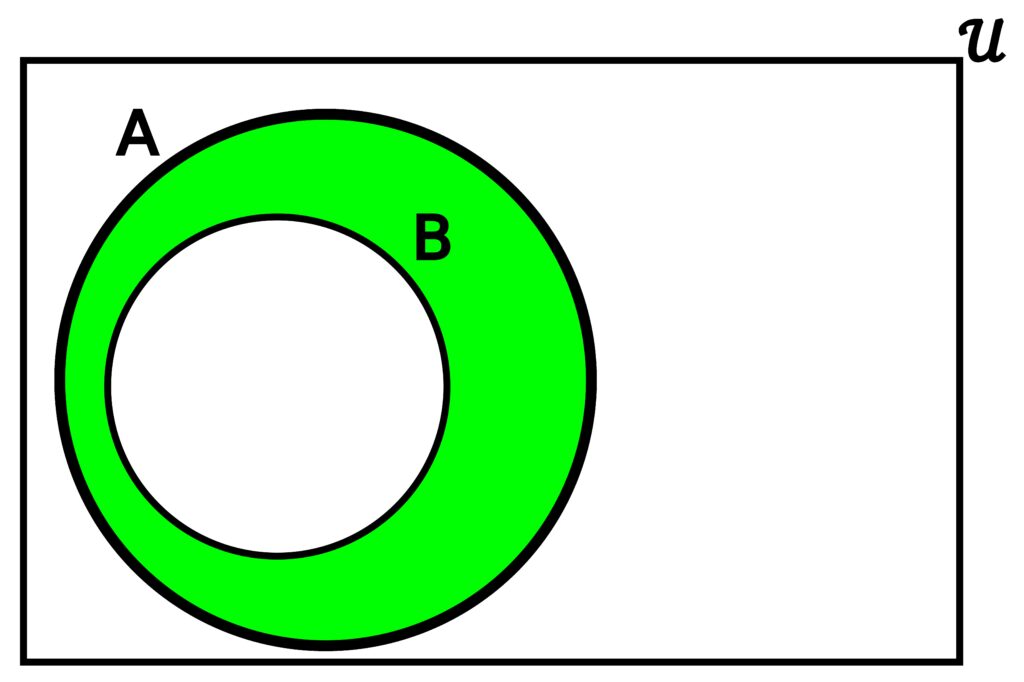
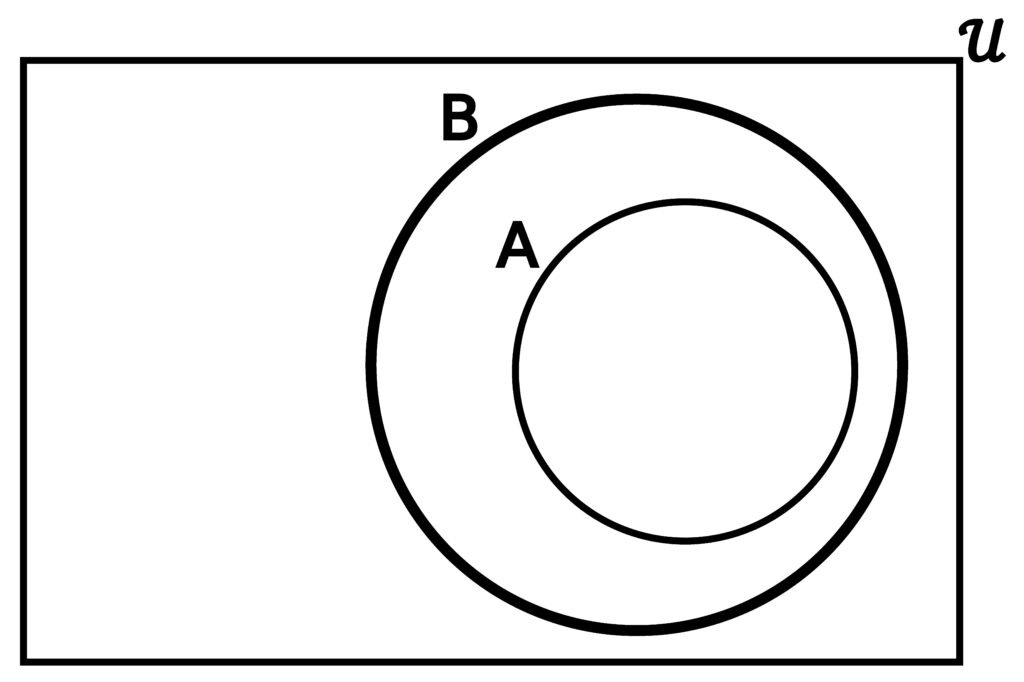
Figure 3.4.7: Reconsider the difference A – B when one of A or B is entirely contained within the other. In (a), we see what happens when B is a subset of A. The region inside A, but outside B is colored green because that regions represents elements in A that are not in B (which satisfy the definition of A – B.) In (b), since everything in A is also in B, we would have to remove every element in A in order to get the set A – B. Thus, there would be nothing in A – B, meaning we would be left with the empty set ∅.
Example 3.4.10
Consider the following sets:
| N | = | { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 98, 99, 100 } |
| S | = | { 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 } |
| E | = | { 0, 4, 16, 36, 64, 100 } |
where N is the universal set being used.
We that by definition, we have that
S – E = { 1, 9, 25, 49, 81 }
since we are trying to remove all of the even perfect squares from S.
However, notice that since every element in E is also an element in S, when we determine E – S, we must remove every element in E. Basically, we start with every element in E, and since we are removing every element in E, we are left with nothing in E – S, which is just the empty set:
E – S = ∅.
Based on Example 3.4.8, and on Figure 3.4.5 (b), it seems that if A ⊆ B, then A – B = ∅. Is that true for every single set? In the next section, we’ll start to use element argument style proofs to determine if that is indeed the case, but for now, our intuition on the matter seems clear.
Symmetric Difference
With set difference, we only consider elements that are in A but not in B. Of course with a symmetric difference, we want elements that are either in A and not in B, or in B and not in A.
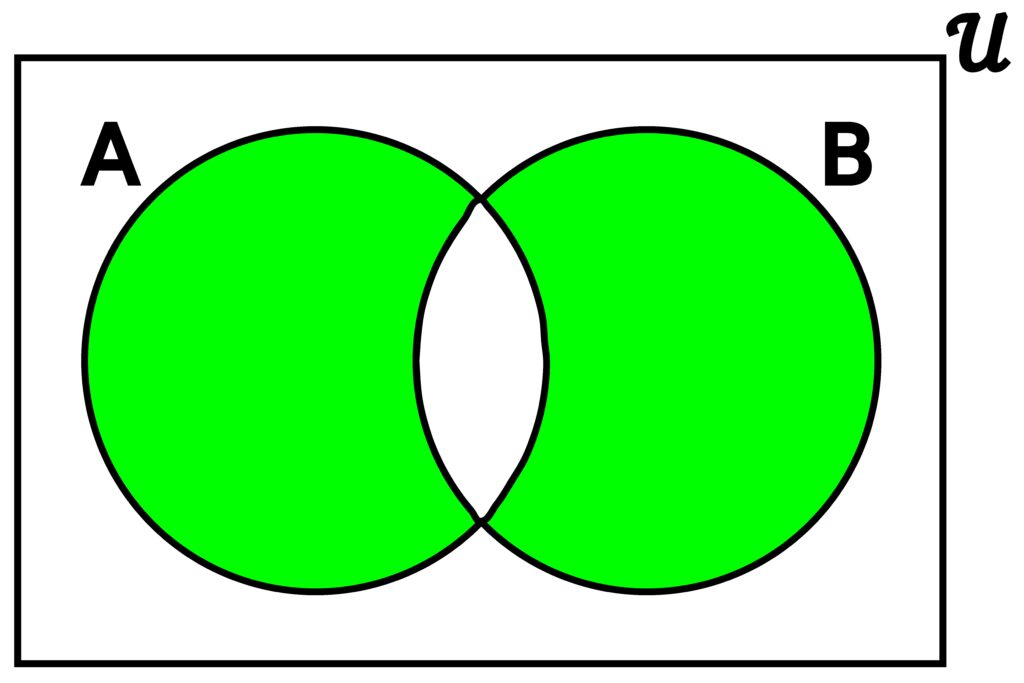
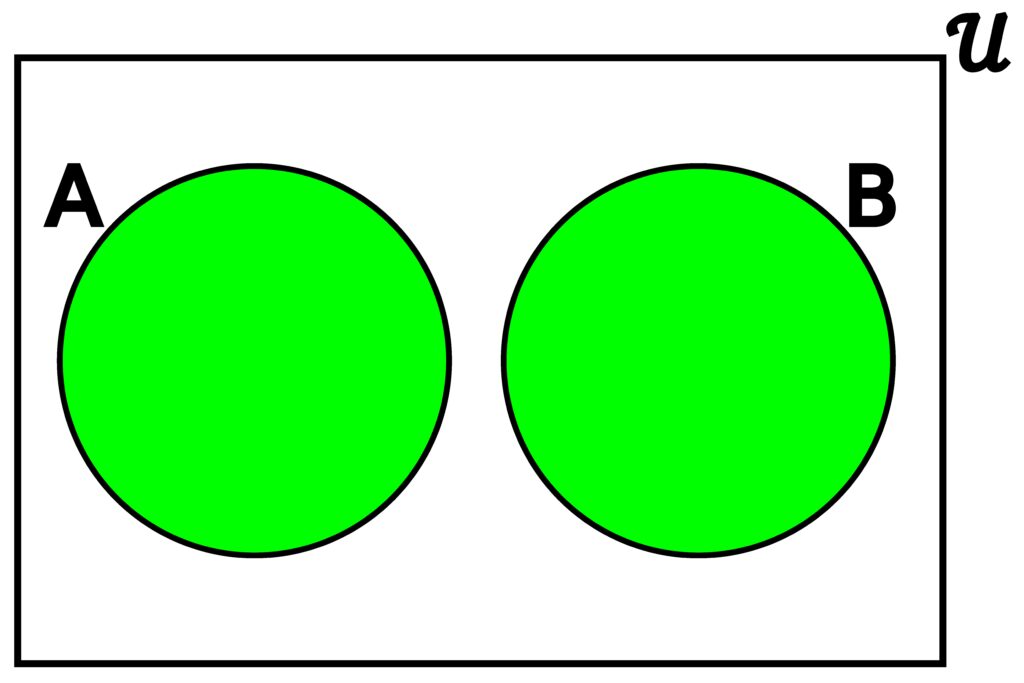
Figure 3.4.8: As long as an element is in one of A or B, but not both, it will be included in the symmetric difference of A and B. (a) shows what happens when there is overlap, and (b) shows what happens when there is no overlap.
Symmetric Difference
Consider two sets A and B containing elements from some universal set 𝒰.
The symmetric difference between A and B, denoted A △ B, is the set
A △ B = { x ∈ 𝒰 | (x ∈ A ∧ x ∉ B) ∨ (x ∉ A ∧ x ∈ B) }
Of course, we can examine given objects to determine membership in such a set:
(x ∈ A △ B) ⟺ [(x ∈ A ∧ x ∉ B) ∨ (x ∉ A ∧ x ∈ B)]
Example 3.4.11
Reconsider the sets
| N | = | { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 98, 99, 100 } |
| S | = | { 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 } |
| C | = | { 0, 1, 8, 27, 64 } |
Is 8 ∈ S △ C? Let’s check the necessary conditions:
| 8 ∈ S = 0 | 8 ∉ S = 1 | 8 ∈ C = 1 | 8 ∉ C = 0 |
| 8 ∈ S ∧ 8 ∉ C = 0 ∧ 0 = 0 | 8 ∉ S ∧ 8 ∈ C = 1 ∧ 1 = 1 |
(8 ∈ S ∧ 8 ∉ C) ∨ (8 ∉ S ∧ 8 ∈ C) = 0 ∨ 1 = 1
Because
(8 ∈ S ∧ 8 ∉ C) ∨ (8 ∉ S ∧ 8 ∈ C) = 1
we have that 8 ∈ S △ C as desired.
We can ask the same thing of 64. Let’s run through the above calculations again, this time using x = 64:
| 64 ∈ S = 1 | 64 ∉ S = 0 | 64 ∈ C = 1 | 64 ∉ C = 0 |
| 64 ∈ S ∧ 64 ∉ C = 1 ∧ 0 = 0 | 64 ∉ S ∧ 64 ∈ C = 0 ∧ 1 = 0 |
(64 ∈ S ∧ 64 ∉ C) ∨ (64 ∉ S ∧ 64 ∈ C) = 0 ∨ 0 = 0.
Because
(64 ∈ S ∧ 64 ∉ C) ∨ (64 ∉ S ∧ 64 ∈ C) = 0,
we have that 64 ∉ S △ C.
Examining all elements in N, we see that
S △ C = { 4, 8, 9, 16, 25, 27, 36, 49, 81, 100 }.
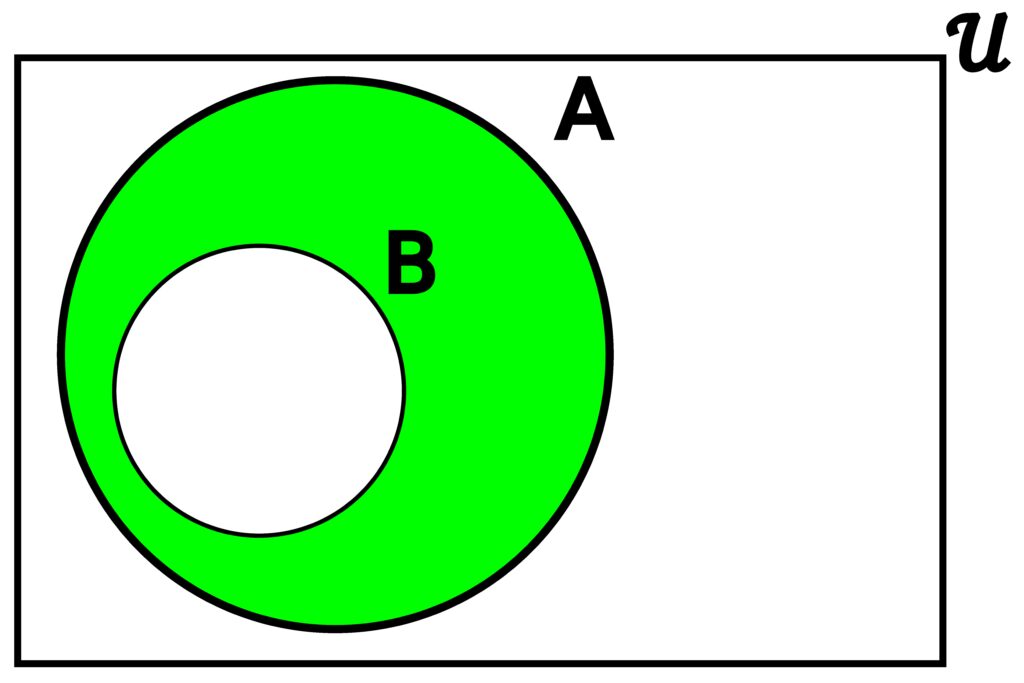
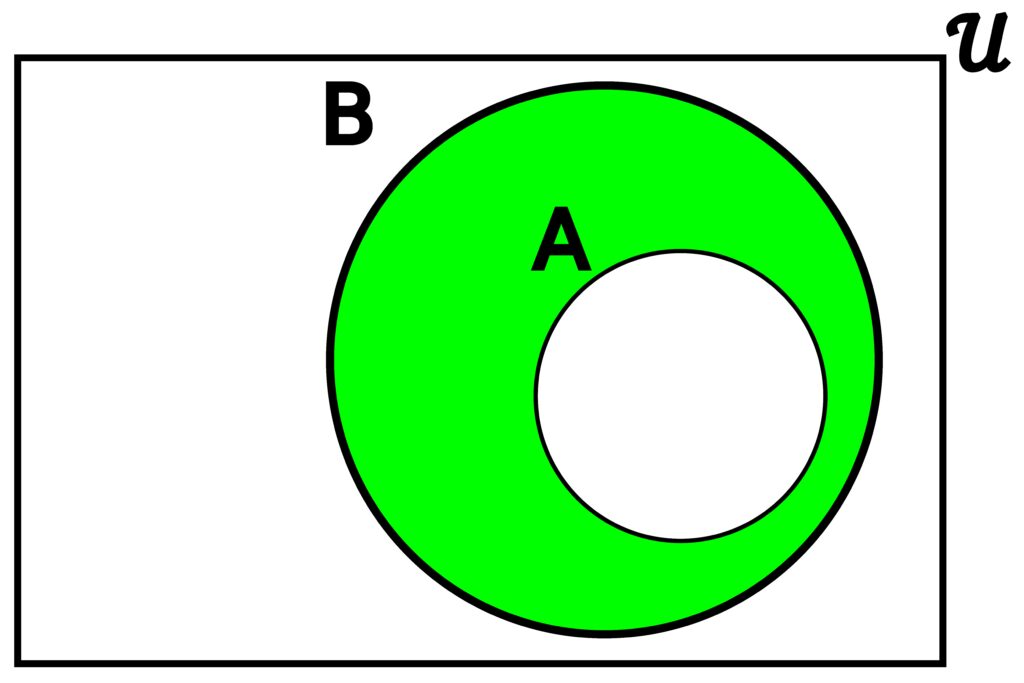
Figure 3.4.9: When one set is a subset of the other, the symmetric difference acts will essentially carve out elements within the subset from the larger set. In (a), we see what happens when B ⊆ A. In (b), we see what happens when A ⊆ B. It’s called a symmetric difference because it’s essentially a difference between the larger set and the subset.
Example 3.4.12
Consider the sets
| N | = | { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 98, 99, 100 } |
| S | = | { 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 } |
| E | = | { 0, 4, 16, 36, 64, 100 } |
where N is the universal set in question.
We see that
S △ E = { 1, 9, 25, 49, 81 }.
Since we only want elements that are in S and not E, or elements that are in E and not S, we also have that
E △ S = { 1, 9, 25, 49, 81 }
as well.
We saw in Example 3.4.# that S △ E and E △ S ended up being the exact same set. Is that always the case? In the next section, we’ll use an element argument to demonstrate that this observation does indeed hold in general.
Multiple Unions and Intersections
We can combine as many sets into a new set as we want. However, before we start combining multiple sets into one, we should recognize that dealing with multiple sets can be cumbersome. First of all, imagine having to deal with multiple sets with a wide variety of names that were hard to track. We can mitigate this issue by coming up with a naming schema that makes each set we’re dealing with easy to track.
Index Set, Index
Consider some universal set 𝒰.
Let I be a non-empty set of objects that are not necessarily taken from 𝒰, and for each i ∈ I, let
Ai ⊆ 𝒰.
The set I is called an index set, and every i ∈ I is called an index.
Before looking at an example, let’s stress the fact that an index set is basically used to enumerate and track sets, and so does not necessarily need to be taken from some universal set (though it could be taken from it’s own particular universal set.)
Example 3.4.13
Consider the universe Z of all whole numbers, including 0 and all negative whole numbers
Z = { 0, 1, -1, 2, -2, 3, -3, 4, -4, … }.
We could deal with a number of sets called A, B, C, D, and E where
| A | = | { 2, 4, 6, 8, 10 } |
| B | = | { -1, 0, 1, 2, 3, 4, 5 } |
| C | = | { 1, 2, 7, 8 } |
| D | = | { 1, 3, 4 } |
| E | = | { -5, -12, -13 } |
We could even have more exotic names like so:
| Λ | = | { 2, 4, 6, 8, 10 } |
| M | = | { -1, 0, 1, 2, 3, 4, 5 } |
| Φ | = | { 1, 2, 7, 8 } |
| Ψ | = | { 1, 3, 4 } |
| ♣ | = | { -5, -12, -13 } |
However, this would be unnecessarily tedious (though there may be times where such names would be useful.)
Instead, what we could do is instead recognize that since we are dealing with 5 sets, we could come up with an index set containing 5 elements like so:
I = { 1, 2, 3, 4, 5 }.
Then, instead of using 5 different set names, we can simply use one symbol, but marked with the indices from the index set like so:
| A1 | = | { 2, 4, 6, 8, 10 } |
| A2 | = | { -1, 0, 1, 2, 3, 4, 5 } |
| A3 | = | { 1, 2, 7, 8 } |
| A4 | = | { 1, 3, 4 } |
| A5 | = | { -5, -12, -13 } |
Notice that in this case, we have that
| A1 ⊆ Z | A2 ⊆ Z | A3 ⊆ Z | A4 ⊆ Z | A5 ⊆ Z |
but we also have that I ⊆ Z, even though we don’t need that to be the case.
Example 3.4.14
Reconsider the set
Z = { 0, 1, -1, 2, -2, 3, -3, 4, -4, … }.
Now consider the index set
I = { a, b, c, d, e }.
Then we could have the following sets:
| Aa | = | { 2, 4, 6, 8, 10 } |
| Ab | = | { -1, 0, 1, 2, 3, 4, 5 } |
| Ac | = | { 1, 2, 7, 8 } |
| Ad | = | { 1, 3, 4 } |
| Ae | = | { -5, -12, -13 } |
where
| Aa ⊆ Z | Ab ⊆ Z | Ac ⊆ Z | Ad ⊆ Z | Ae ⊆ Z |
but this time, I ⊈ Z.
Example 3.4.15
Once again, reconsider the set
Z = { 0, 1, -1, 2, -2, 3, -3, 4, -4, … }.
We can make the index set anything we want, such as
I = { 1, a, x, ⊝, ☆ }.
Then we have
| A1 | = | { 2, 4, 6, 8, 10 } |
| Aa | = | { -1, 0, 1, 2, 3, 4, 5 } |
| Ax | = | { 1, 2, 7, 8 } |
| A⊝ | = | { 1, 3, 4 } |
| A☆ | = | { -5, -12, -13 } |
where
| A1 ⊆ Z | Aa ⊆ Z | Ax ⊆ Z | A⊝ ⊆ Z | A☆ ⊆ Z |
This time, even though we have that I ⊈ Z, there is at least one element in I that is also in Z.
It’s worth noting that this kind of index set is impractical, and so will not be used going forward unless there is some niche application where it would be useful.
With an index set to help us, working with multiple sets is easy.
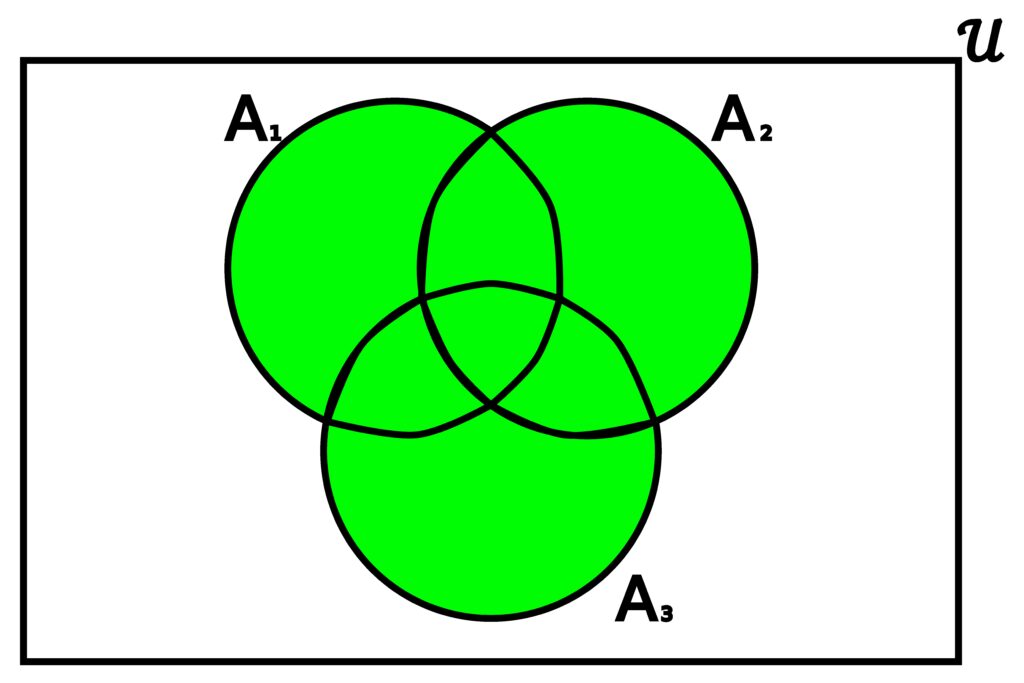
Figure 3.4.10: When dealing with multiple sets A1, A2, and A3, we can take every single element from every set, and stick them into a new set, which we refer to as the union of all the sets.
Multiple Union
Consider a universal set 𝒰, along with an index set I where for each i ∈ I, we have that
Ai ⊆ 𝒰.
The multiple union of all Ai is denoted
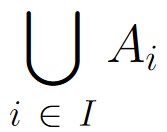
If the index set is defined using the whole numbers
I = { 1, 2, 3, …, n },
then we can write this multiple union as
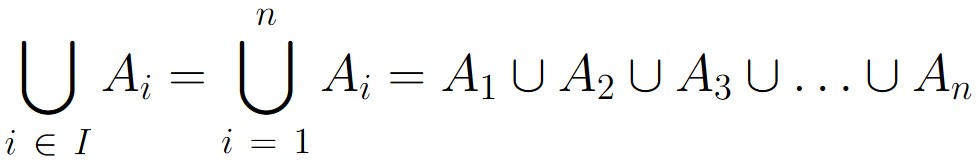
As always, if we want to check to see if a given object is in this set, all we have to do is check to see if that object is in at least one of the sets making up the multiple union:
Of course, if the index set uses whole numbers starting from 1, and ending at n, we can instead write this logical equivalency as
Example 3.4.16
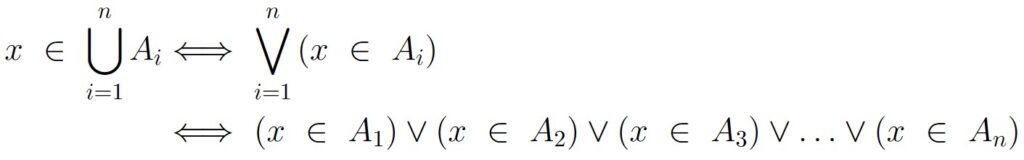
Once again, reconsider the set
Z = { 0, 1, -1, 2, -2, 3, -3, 4, -4, … }.
with the following index set
I = { 1, 2, 3, 4 }.
along with the following sets.
| A1 | = | { 2, 4, 6, 8, 10 } |
| A2 | = | { -1, 0, 1, 2, 3, 4, 5 } |
| A3 | = | { 1, 2, 4, 7, 8 } |
| A4 | = | { 1, 3, 4 } |
Is 8 in the multiple union of A1, A2, A3, and A4? We can check to see if 8 is in at least one of them:
| (8 ∈ A1) ∨ (8 ∈ A2) ∨ (8 ∈ A3) ∨ (8 ∈ A4) | = | 1 ∨ 0 ∨ 1 ∨ 0 |
| = | 1 |
As such, we see that 8 is indeed in the multiple union of A1, A2, A3, and A4.
However, when it comes to a number like 13, we see that
| (13 ∈ A1) ∨ (13 ∈ A2) ∨ (13 ∈ A3) ∨ (13 ∈ A4) | = | 0 ∨ 0 ∨ 0 ∨ 0 |
| = | 0 |
and so 13 is not in the multiple union of A1, A2, A3, and A4.
We can just go ahead and determine the entire multiple union:
| A1 ∪ A2 ∪ A3 ∪ A4 | = | { 2, 4, 6, 8, 10 } ∪ { -1, 0, 1, 2, 3, 4, 5 } ∪ { 1, 2, 4, 7, 8 } ∪ { 1, 3, 4 } |
| = | { 2, 4, 6, 8, 10, -1, 0, 1, 2, 3, 4, 5, 1, 2, 4, 7, 8, 1, 3, 4 } | |
| = | { -1, 0, 1, 1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 6, 7, 8, 8, 10 } | |
| = | { -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 10 } |
Another way we can write the set representing the multiple union is as follows:
{ x ∈ 𝒰 | ∃i ∈ I [x ∈ Ai] }
Naturally, there is an intersection counterpart the the multiple union.
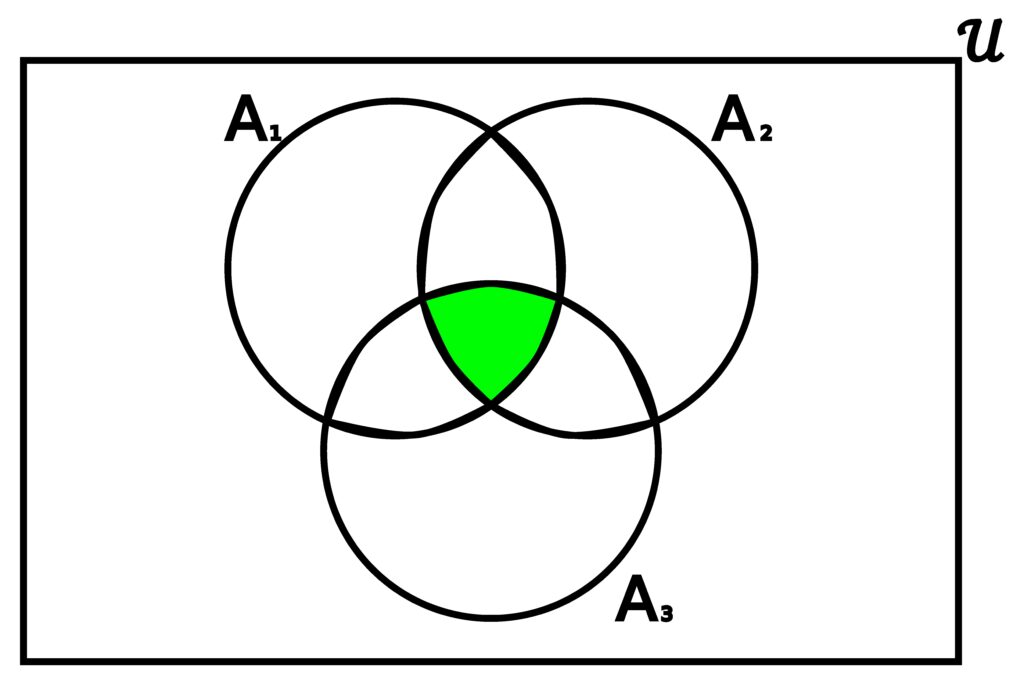
Figure 3.4.11: When dealing with multiple sets A1, A2, and A3, we can take all elements contained in all 3, and stick them into a new set, which we refer to as the intersection of all the sets.
Multiple Intersection
Consider a universal set 𝒰, along with an index set I where for each i ∈ I, we have that
Ai ⊆ 𝒰.
The multiple intersection of all Ai is denoted
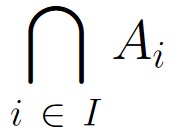
If the index set is defined using the whole numbers
I = { 1, 2, 3, …, n },
then we can write this multiple union as
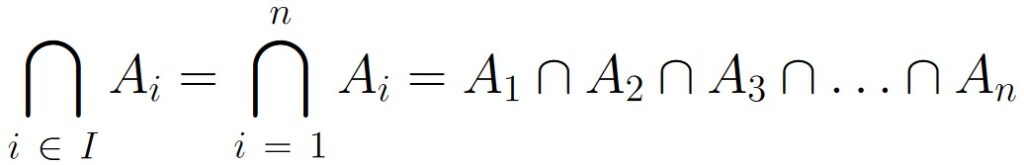
Checking if a given object is in the multiple intersection of a collection of sets works nearly the same as checking if it’s in the multiple union, but we need to make sure the object is in all sets, which we can check with multiple and operations:
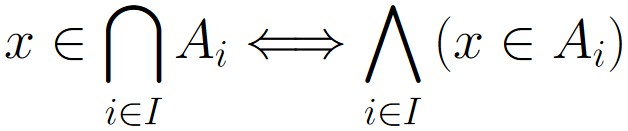
Of course, if the index set uses whole numbers starting from 1, and ending at n, we can instead write this logical equivalency as
Example 3.4.17
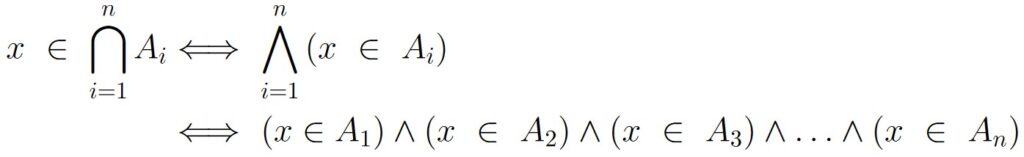
Once again, reconsider the set
Z = { 0, 1, -1, 2, -2, 3, -3, 4, -4, … }.
with the following index set
I = { 1, 2, 3, 4 }.
along with the following sets.
| A1 | = | { 2, 4, 6, 8, 10 } |
| A2 | = | { -1, 0, 1, 2, 3, 4, 5 } |
| A3 | = | { 1, 2, 4, 7, 8 } |
| A4 | = | { 1, 3, 4 } |
Is 4 in the multiple intersection of A1, A2, A3, and A4? We can check to see if 4 is in at least one of them:
| (4 ∈ A1) ∧ (4 ∈ A2) ∧ (4 ∈ A3) ∧ (4 ∈ A4) | = | 1 ∧ 1 ∧ 1 ∧ 1 |
| = | 1 |
As such, we see that 4 is indeed in the multiple intersection of A1, A2, A3, and A4.
However, when it comes to a number like 8, we see that
| (8 ∈ A1) ∧ (8 ∈ A2) ∧ (8 ∈ A3) ∧ (8 ∈ A4) | = | 1 ∧ 0 ∧ 1 ∧ 0 |
| = | 0 |
and so 8 is not in the multiple union of A1, A2, A3, and A4.
We can just go ahead and determine the entire multiple intersection:
| A1 ∩ A2 ∩ A3 ∩ A4 | = | { 2, 4, 6, 8, 10 } ∩ { -1, 0, 1, 2, 3, 4, 5 } ∩ { 1, 2, 4, 7, 8 } ∩ { 1, 3, 4 } |
| = | { 2, 4 } ∩ { 1, 2, 4, 7, 8 } ∩ { 1, 3, 4 } | |
| = | { 2, 4 } ∩ { 1, 3, 4 } | |
| = | { 4 } |
Another way of writing the set representing the multiple intersection is as follows:
{ x ∈ 𝒰 | ∀i ∈ I [x ∈ Ai] }