What Are Rook Polynomials?

Some Motivating Examples

Before introducing what Rook Polynomials actually are, I want to motivate their existence by discussing some example problems.

Example 1: How many ways are there to assign band positions?

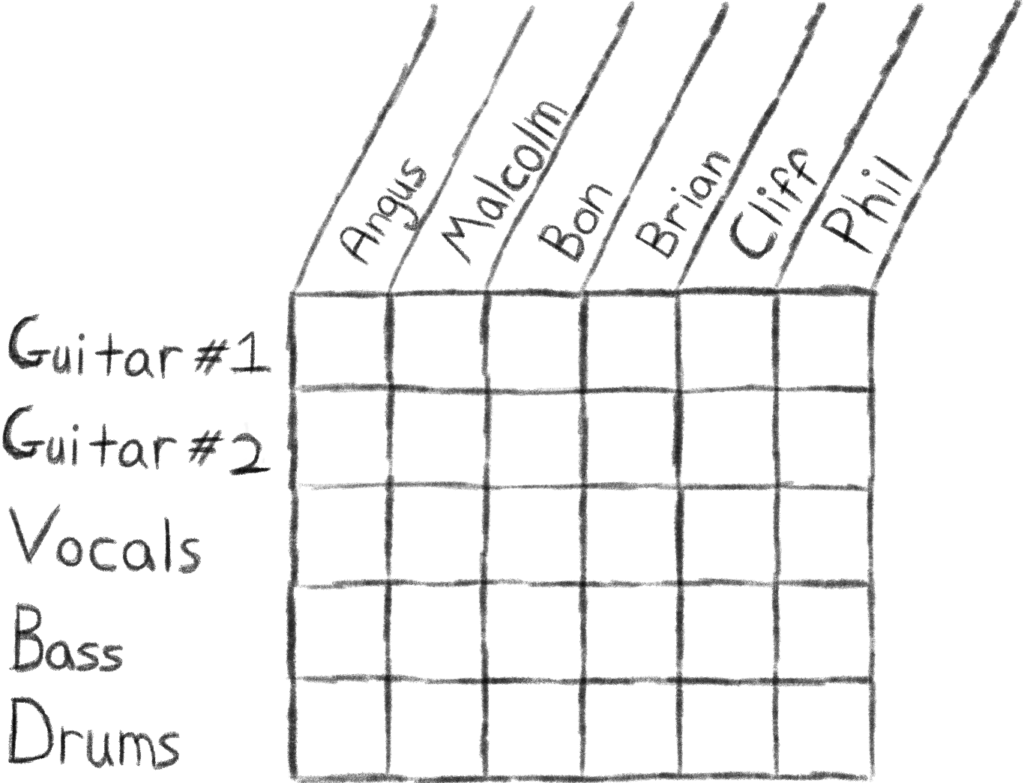
Let’s say that there are 6 people wanting to form a band and that their names happen to be Angus, Malcolm, Bon, Brian, Cliff, and Phil (which were – of course – chosen randomly without any outside influences whatsoever.) They want to form a rock band, so naturally they need two guitarists, one singer, one bassist, and one drummer. Lets see if we can visualize this situation:

To start to get a foothold on this problem, let’s just go ahead and assign one person to one position, and see what happens. For example, maybe we assign Angus to be Guitar #1. We’ll color in the square corresponding to Angus and Guitar #1 green to represent the fact that Angus was assigned to that position. Note that once we make this assignment, Angus can’t simultaneously perform another role in the band, so we’ll color the other squares in Angus’s column red. Likewise, no other person can assume the role of Guitar #1 because it was just assigned, so we’ll color the other squares in the Guitar #1 row red as well.

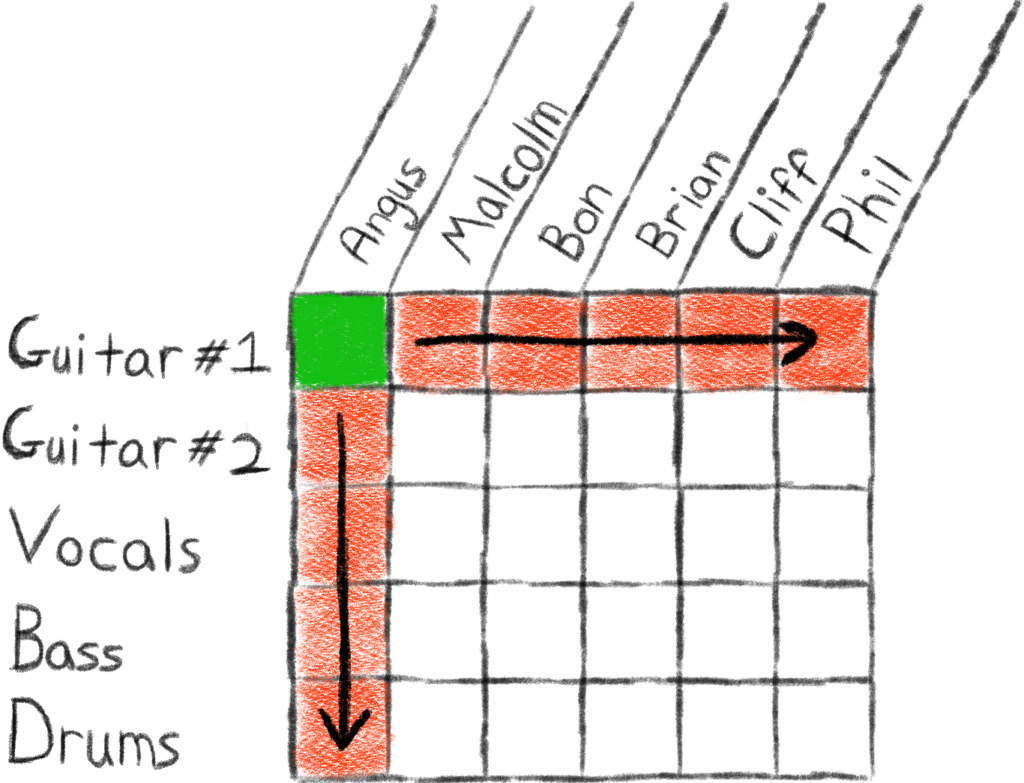
What we’re left with is a sort of sub-grid, representing the rest of the assignments that can be made. Any of the squares in the white region of the grid can be colored green to represent another assignment.

Let’s continue making these assignments. Perhaps we (randomly of course) assign Cliff to handle the Bass position. Again, we color the square corresponding to Cliff and Bass green to represent the fact that Cliff was assigned to handle the Bass position. Same as before, once Cliff is assigned a position, he can’t simultaneously handle other positions, so we’ll color all other squares in Cliff’s column red. Likewise, once the Bass is assigned to a person, it can’t be handled by any other person, so we’ll color in all the other squares in the Bass row red as well.

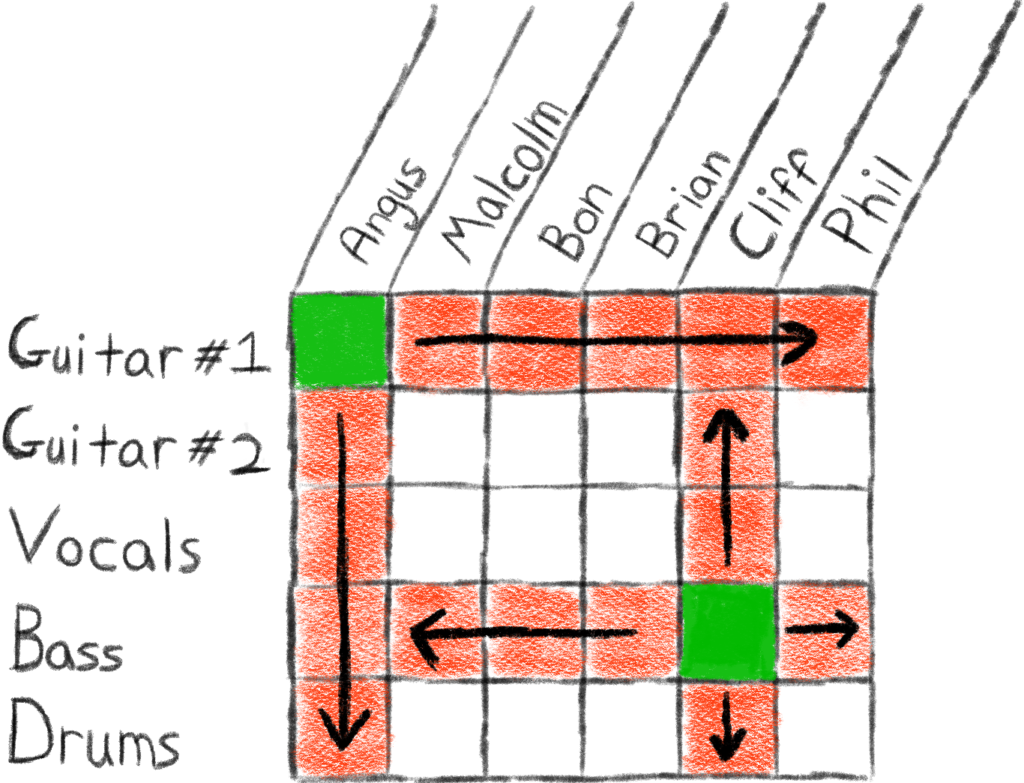
Continuing on with this process, eventually all positions in the band will be assigned to one of the band members. For example, we may come up with the following (totally random) assignment:

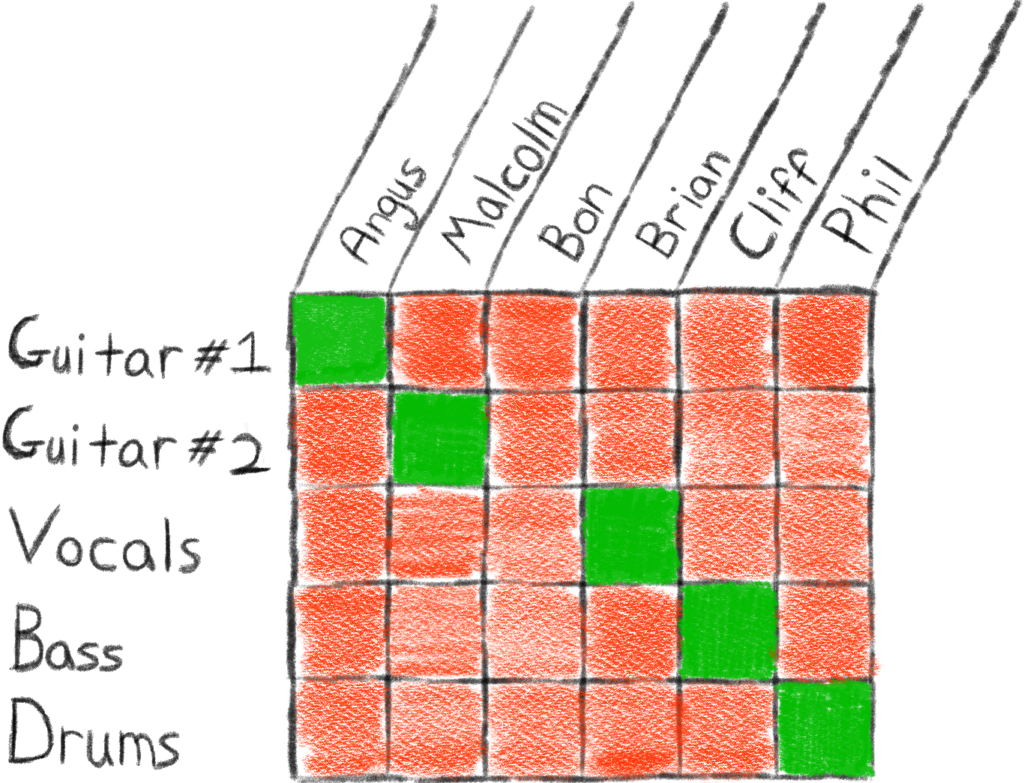
So, it looks like we’ve made the following assignments:

• Angus <-> Guitar #1
• Malcolm <-> Guitar #2
• Bon <-> Unassigned
• Brian <-> Vocals
• Cliff <-> Bass
• Phil <-> Drums

Note that one of the band members was sadly left out. Even though one of the people was left out of the band, we still have a complete band line up, so this is in fact one of the ways to assign band positions. How many ways in total are there to make these assignments? Another way we could have made the assignments is as follows:

• Angus <-> Vocals
• Malcolm <-> Guitar #1
• Bon <-> Drums
• Brian <-> Bass
• Cliff <-> Guitar #2
• Phil <-> Unassigned

Ideally we’d like to avoid exhaustively checking and counting each and every single possible valid assignment by drawing out these grids, and coloring squares. Is there a better way? Yes, but before we talk about it, let’s consider another, simpler example.

Example 2: How many ways are there to assign a technician to monitor networking equipment?

Let’s say we’re running a business, and our company network is maintained by three pieces of equipment: a server, a set of switches, and a firewall. Furthermore, suppose we have three technicians in our IT department: Alice, Bill, and Charlie. Everyday, we assign one of these technicians to configure, monitor, and maintain one of the pieces of equipment needed to run our company network. Again, we can draw another grid to represent how we can make these daily assignments.

Just like in the band example, we can color a square green to represent a chosen assignment, and we color all other squares in that same row and column red to represent restricted assignments. One such assignment is shown below.

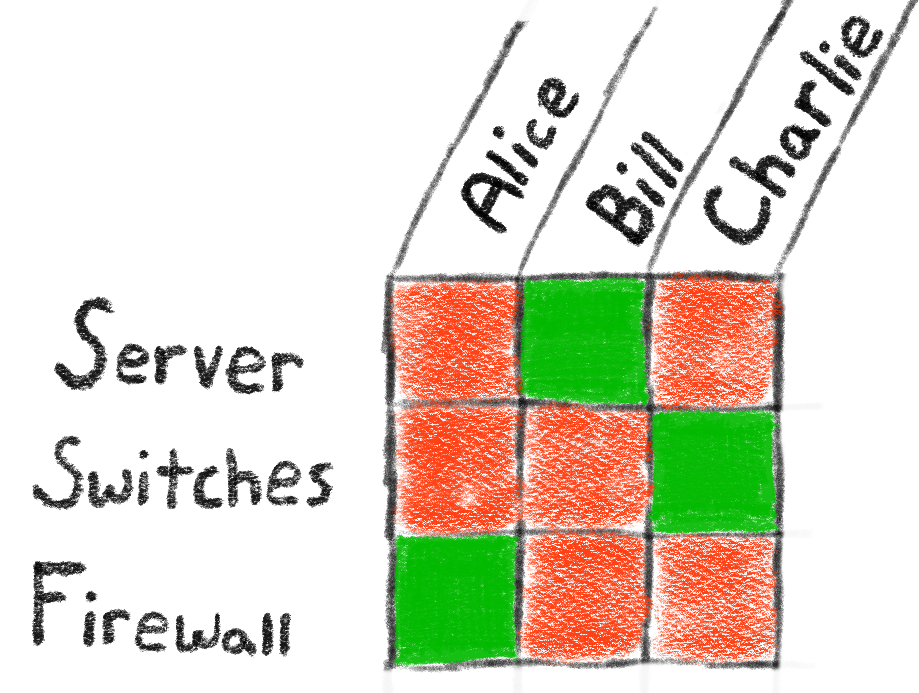
In this case, we’ve made the following assignments:

• Alice <-> Firewall
• Bill <-> Server
• Charlie <-> Switches

Note that because there are the same number of employees as the number of equipment, every employee gets utilized, and every piece of equipment gets monitored.

Because this is a 3-by-3 grid instead of a 5-by-6 grid, we can exhaustively count the number of ways to make these assignments more quickly than in the previous example. We can do this using a little bit of case work.

Case 1: Alice monitors the server

In this case, we have two choices to make: either Bill monitors the switches (thus forcing Charlie to monitor the firewall), or Bill monitors the firewall (forcing Charlie to monitor the switches.) So in this case there are 2 possible choices.

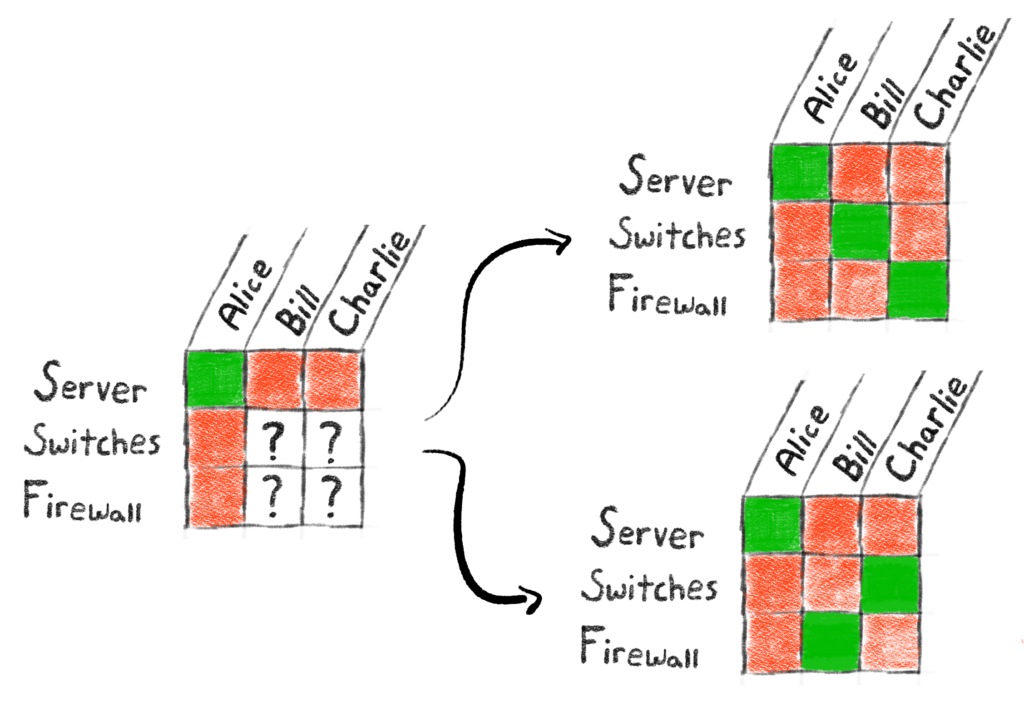
Case 2: Alice monitors the switches

Again, we see that there are 2 ways to assign Bill and Charlie to monitor the rest of the equipment.

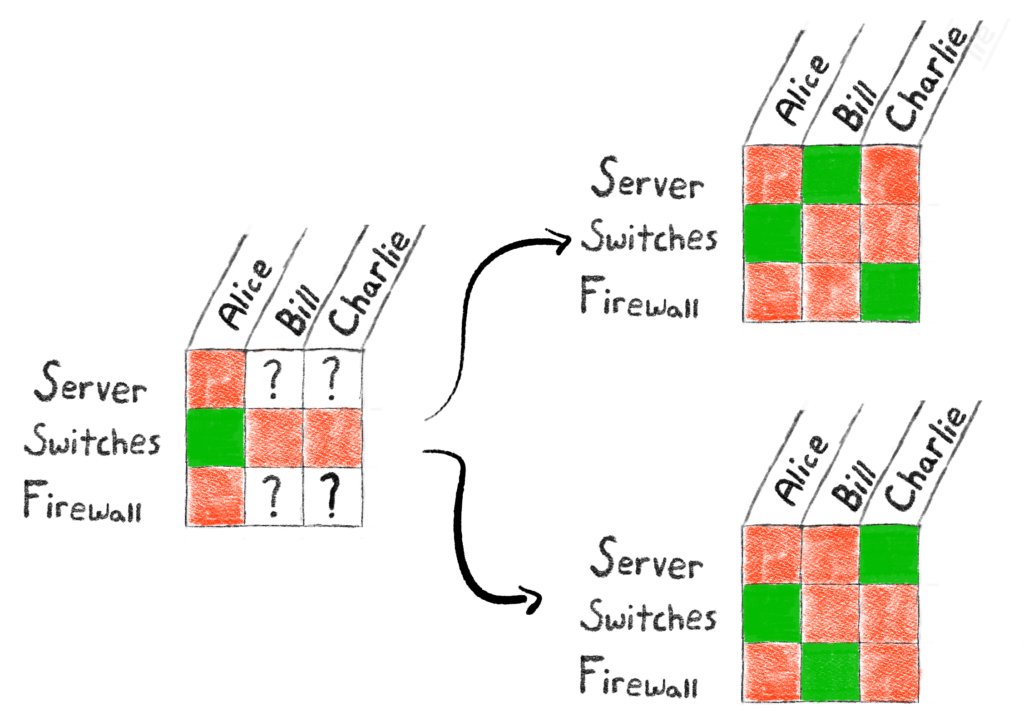
Case 3: Alice monitors the firewall

And of course, we see there are 2 ways ways to assign Bill and Charlie to monitor the other equipment.

So, in total we’ve counted

ways to assign all 3 technicians to to monitor all 3 pieces of equipment.

Other Possibilities

Let’s continue examining the second example. Let’s suppose one of the employees calls in sick, leaving us with only 2 technicians to monitor equipment. Unfortunately when that happens, 1 piece of equipment will be left unmonitored that particular day because we would not have enough technicians. We can still count the number of ways to make assignments by considering the different cases.

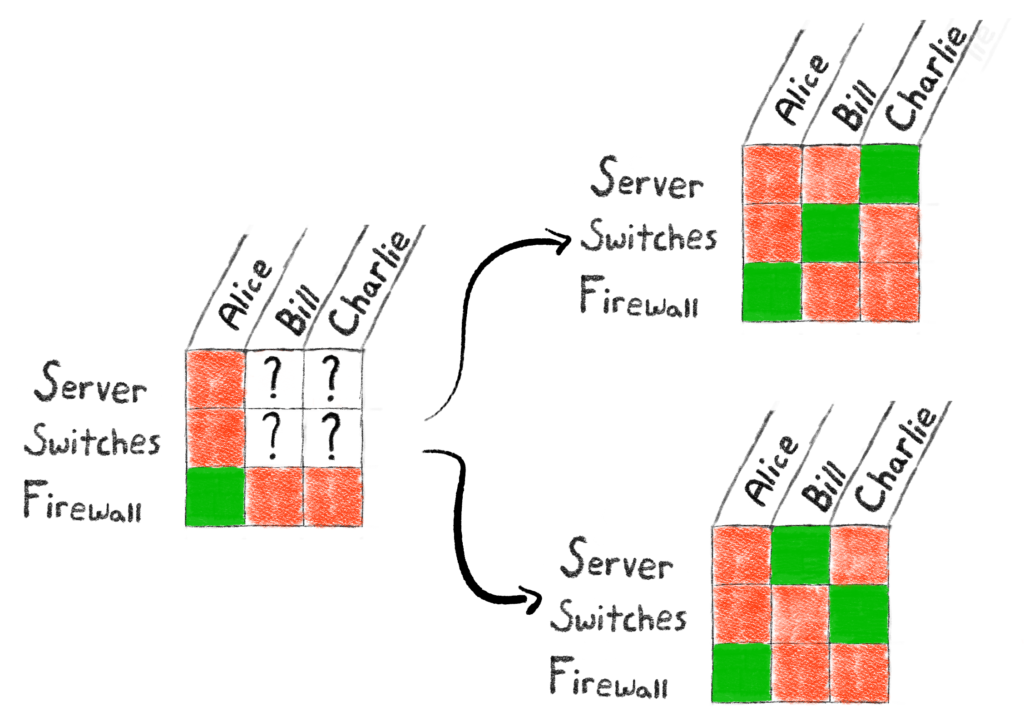
Case 1: Alice calls in sick

Since Alice is not present, we can color her entire column red to signify, that those assignments are restricted. This leaves Bill and Charlie, each of which can be assigned one of three pieces of equipment.

We can make

possible assignments when Alice is not present. We can picture this using our grid format, though this is becoming a bit too involved and cumbersome.

Case 2: Bill calls in sick

Instead of drawing (almost) the same picture again, let’s take advantage of the symmetry of the situation, and realize there are still 6 ways to assign Alice and Charlie to a piece of equipment (leaving one unmonitored again.)

Case 3: Charlie calls in sick

Again, taking advantage of the symmetry yields a total of 6 ways to assign Alice and Bill to a piece of equipment, leaving one unmonitored.

Therefore, the total number of ways to assign 2 employees to monitor piece of equipment is

The Final Answer for Example 2

Ok, so now we have a good idea of what’s going on with these kinds of counting problems. Let’s talk about two more situations involving example 2.

Consider a scenario where two employees call in sick. Then we can only assign that 1 employee to 1 piece of equipment to monitor. There are of course 3 ways to do this. There is 1 out of 3 employees who could arrive, so by the rule of product we have a total of

ways to make the assignment (two pieces of equipment will be left unmonitored in this situation.)

Now consider a scenario where all 3 employees call in sick. Here, there is only 1 possible outcome: all pieces of equipment are left unmonitored. A bit unfortunate, but luckily our company hires the best technicians and uses the best equipment, so we’ve got nothing to worry about!

In summary, including all possible scenarios described above, all of which are independent of each other, we have by the rule of sum that there are

total possible assignments. Not only that, but we’ve also calculated the number of assignments for each possible outcome:

• 0 technicians <-> 1 assignment
• 1 technician <-> 9 assignments
• 2 technicians <-> 18 assignments
• 3 technicians <-> 6 assignments

Tangent: Rooks on a Chess Board

Ok, with the examples out of the way, lets start the discussion. When talking about Rook Polynomials, we are referring to the chess piece. Basically, we’re going to start counting the number of ways to place some number of indistinguishable rooks on a chess board so that they can’t attack one another. The typical chessboard has 8 rows and 8 columns, which is going to require a lot of brute force counting, so we’ll consider a smaller chess board with only 3 rows and 3 columns. Also, since we’re talking about rooks attacking one another on the board, the colors of the squares won’t affect what we’re counting, so we’ll ignore the colors, and use pictures of a white chess board divided into grids to get the point across.

We can break up our counting into case work.

Case One: 0 rooks

This is pretty trivial. When there are 0 rooks, the chessboard can only exist in 1 state (the state where the board has nothing on it.)

Case Two: 1 rook

When dealing with only 1 rook, we don’t have to worry about making sure it won’t be captured by another rook (because there is only 1 rook, and rooks can’t capture themselves.) For our 3-by-3 chess board, there are 9 possible locations for us to place the rook.

Case Three: 2 rooks

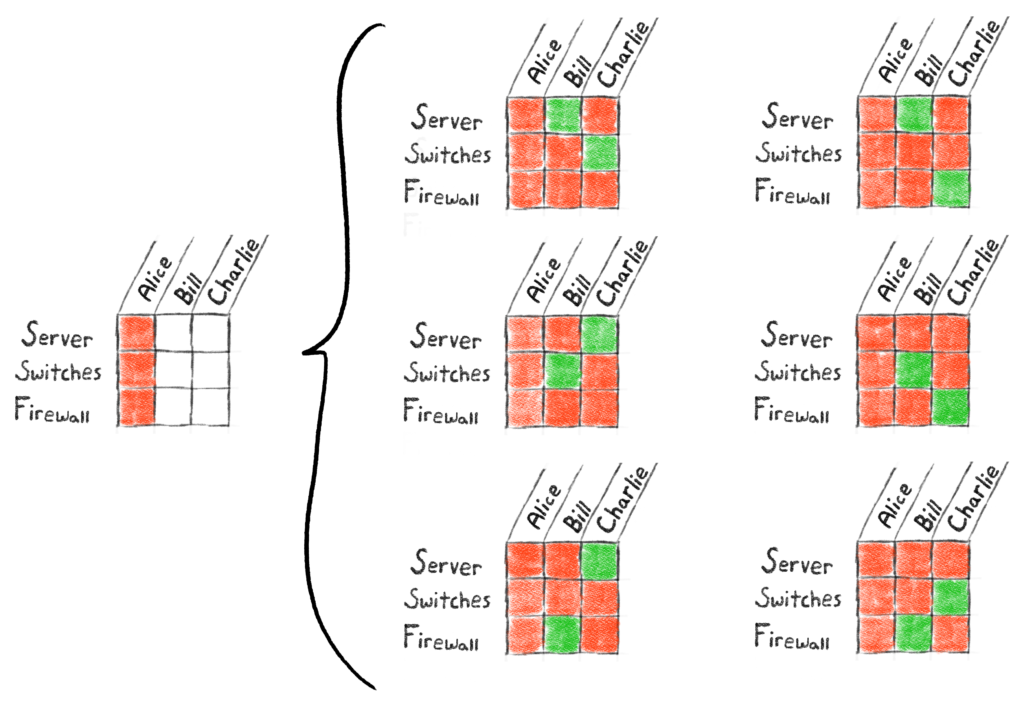
Here, because there are two rooks, we must be careful to place them on the board so they don’t capture each other. Because there are only nine squares, and because the rooks are indistinguishable, a brute force count won’t be too time-consuming. Let’s suppose we place one of the rooks in the upper-left corner of the board.

We’ve colored any square in the same row or column as the first rook red so we know not to place the other rook in any of those squares. This will let us prevent placing the rooks in a way that can lead to attack. Of course, we see that there are 4 ways to place the remaining rook. We can just pick one.

We can picture all possibilities in the following way: this time, we’ll color black any square that represents a previously counted placement, so we can count only new possibilities by placing the second rook only on green squares. Red squares will still represent squares attacked by the first rook. With this coloring scheme, we get the following picture.

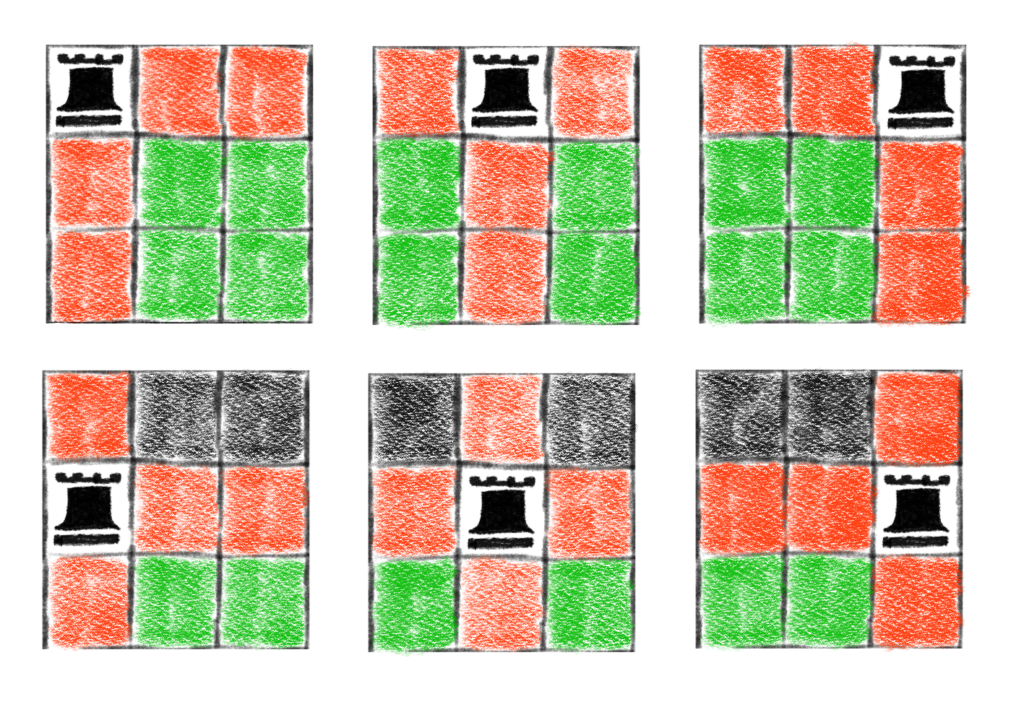
Now all we have to do count green squares.

So, there are 18 different ways to place two rooks on a 3-by-3 board so that they don’t attack each other. Note that we don’t include any pictures with a rook in the bottom row because those positions were already accounted for in the first six scenarios pictured.

Case Four: 3 Rooks

In this case, we can easily enumerate all possibilities by following a similar strategy to case three.

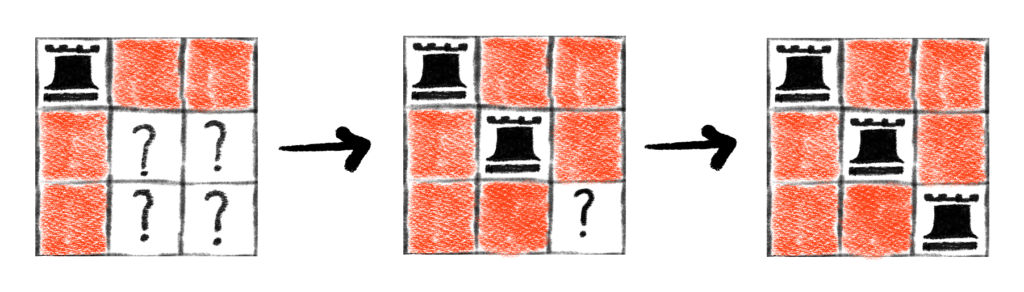
We place one rook at a time, coloring any squares that can be attacked by it red. We then avoid placing any other rook on those red squares. Doing so yields the following picture.

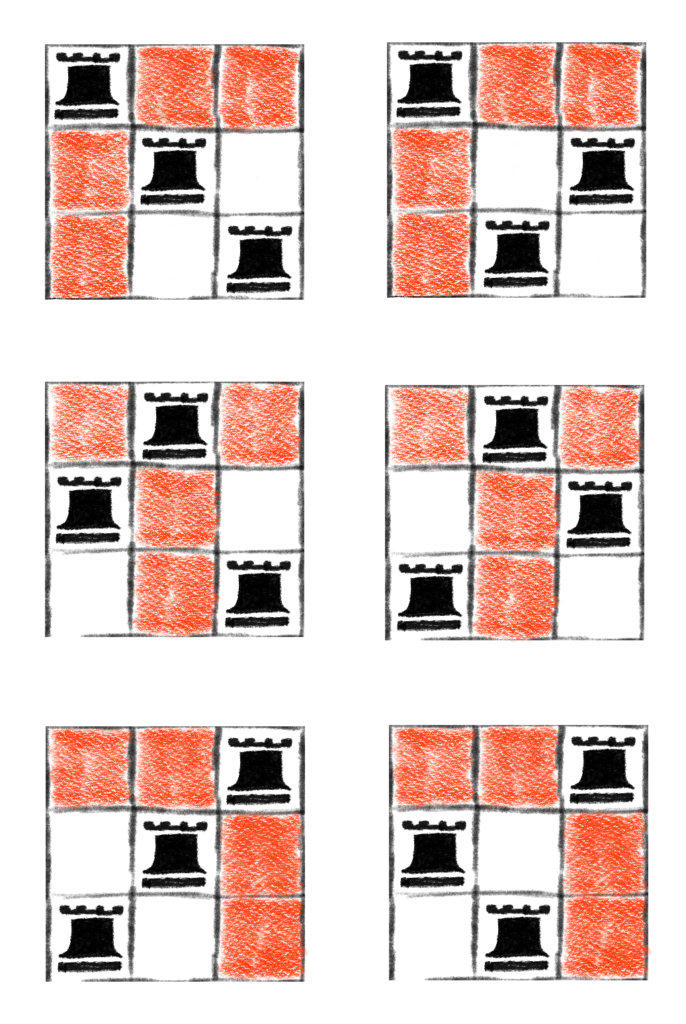
So there are 6 ways to place 3 rooks on a 3-by-3 board in such a way that no rook attacks another rook.

Case Five: 4 or More Rooks

Based off the previous counting, we see that there are 0 ways to place 4, 5, 6, or more rooks on this board.

Summary

So we’ve counted the total number of ways to place any number of rooks on a 3-by-3 board such that no other rook attacks another.

• 0 Rooks <-> 1 way
• 1 Rook <-> 9 ways
• 2 Rooks <-> 18 ways
• 3 Rooks <-> 6 ways
• More than 3 Rooks <-> 0 ways

You may notice that these are the same answers we got for example 2.

Introducing Rook Polynomials

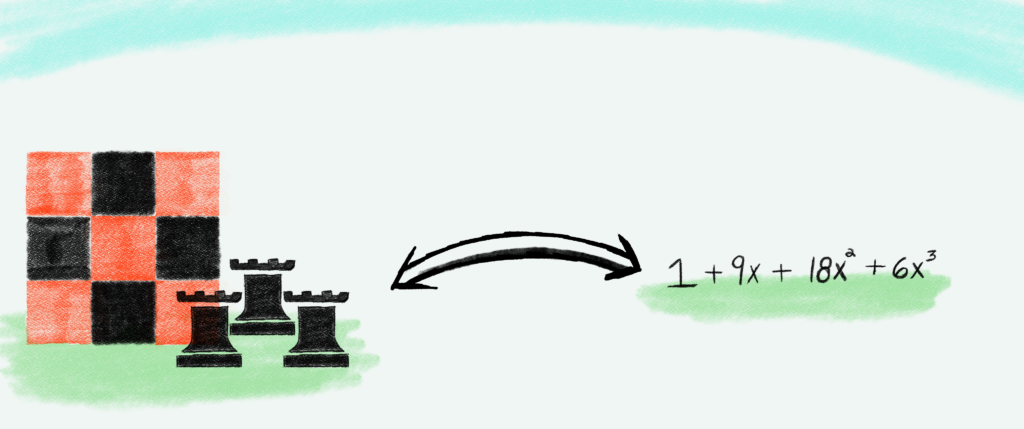
Finally, we can describe Rook Polynomials. For a given chess board, a Rook Polynomial is a polynomial where each term’s exponent represents the number of rooks being placed on that chess board. and each term’s coefficient tells you the number of ways to place rooks on that board such that they don’t attack each other. Put another way:

As an example, here’s the Rook Polynomial for the 3-by-3 chess board:

Looking at this polynomial, we see that the coefficient of the x³ term is 6. This tells us that there are 6 ways to place 3 rooks such that no other rook attacks another. Similarly, the coefficient of the x² term is 18. Thus there are 18 ways to place 2 rooks on a 3-by-3 board.

What’s really awesome about these things is that they are basically telling you the answers to essentially an infinite number of counting problems all at once. All you have to do is look at the term with the appropriate exponent, and then pick off the coefficient. Rook polynomials are one kind of generating function, which are honestly my favorite kinds of functions.

What’s the Connection Between Rook Polynomials and Our Example Problems?

The reason why the answer to our second example is the same as our 3-by-3 chess board is because there is a one-to-one correspondence between placing non-attacking rooks on a 3-by-3 chess board, and assigning at most 3 technicians to monitor 3 pieces of equipment.

Remember, once we assigned a technician to a piece of equipment (or a band person to a band position), we essentially restrict that person from monitoring any other piece of equipment, and we restrict that piece of equipment from being monitored by anyone else. Visually, we colored each row and column red, signifying that those assignments are now restricted.

This is similar to our rook situation. Once a rook is placed on a square, that square’s row and column are restricted from any other rook (or else that rook would be attacked.)

Is There a Better Way of Calculating these Rook Polynomials?

Yes, but this post is long enough. Coming up, we’ll talk about ways to make calculating these polynomials easier. For small chess boards, this method will be easy enough to do by hand, but for large chess boards, we’ll want to automate the calculation using software.