Sets

The mathematical logic that we’ve studied in the previous two chapters is foundational to all types of math. However, as demonstrated in the last few sections of chapter 2, mathematicians rarely layout all of the full gory details when writing proofs. Instead, they rely on axioms, definitions, and previous theorems to work out the desired result. Occasionally, propositional logic may be used when doubts arise to the validity of a given proof, but that too is rare.

Something we’ve hinted at in the previous two chapters is that when we want to validate an argument, we start of some number of premises. Another way of stating this is that we start off with some initial collection, or set, of premises, and from those premises, we hopefully arrive at the desired conclusion. The group of premises we start off with may change from one argument to another, but in any case, we have a starting collection of premises no matter what argument we’re trying to build up.

The idea of a collection, or set, of objects underlies almost all of mathematics, whether that be a collection of premises (in mathematical logic), a collection of points (in geometry), a collection of possible outcomes for an experiment (in probability), or a collection of outputs for some given collection of inputs (mathematical relations). In this chapter, we start to define and work with these collections of objects, and what we can do with collections of objects in general. Even though mathematicians rarely describe all of the formal logic used in their arguments, any set theoretic aspects are almost always explicitly laid out. Hence, getting a good understanding of Set Theory will be vital in learning to not only do mathematics, but to read mathematics as well.

Trying to precisely define a set can be rather tricky. While there are formal definitions and axioms, here we will rely on our intuition. Even without a formal specification, we can still derive many useful results that still hold when scrutinized.

In this section, we’ll learn what a set is (intuitively) and how to describe what kinds of things are in the set.

Intuitively Defining a Set

Sets, or collections, of objects abound in daily life. We could speak of the set of fruits available for purchase at a local grocery store, the set of birds native to North America, the set of components used to build a specific computer, the set of roads from New York to Los Angeles, and so on. We can make note of a couple of things here:

The order in which we may list the items in the collection doesn’t appear to be relevant. If we simply want to know what kinds of birds are native to North America, we can list the Wild Turkey before we list the Sandhill Crane, or we could list the Sandhill Crane before the Wild Turkey.
If we accidentally list an item more than once, that also doesn’t affect the set we’re dealing with. For example, if we list I-80 W twice by accident, it doesn’t change the fact that I-80 W is still a road between New York and Los Angeles. Sometimes, we may care when planning a trip, but not if we just want to know what roads exist between New York and Los Angeles.
However, if we miss an object (if it’s listed 0 times) that does affect our set because then our set is not complete. For example, if a local grocery store sells mangoes, but forgets to advertise them, then they may lose out on customers who want to purchase mangoes.

As such, the order in which we list elements from a set is irrelevant. The number of times we list an element from a set is also irrelevant. All we care about is whether or not an object is in a set or not.

Sets of objects also appear frequently in mathematics. We could speak of the set of numbers used to count objects, the set of points that make up a line in space, the collection of parabolas with real roots, the set of solutions to a system of equations, and so forth. Again, we don’t really care about the order in which these objects can be listed out, and we also don’t care if some objects from the set are listed more than once. However, in order to be a complete description, every possible object must be listed at least once.

Set, Element, Member

A set is an unordered collection of well-defined objects.

Each object within the set is called an element, or member, of that set.

We write

x ∈ A

to denote that object x is a member of the set A. On the other hand, if some object denoted y was not in A, then we would write

y ∉ A.

By well-defined, what we mean is that, if presented a description of some set A, we are able to determine if some given object, which we’ll refer to as x, is an element of A under scrutiny.

Example 3.1.1

Suppose we were interested in forming sets of Major League Baseball players.

What kinds of players would we include if we wanted to form the set of “outstanding left-fielders”? The first thing we would need to do is figure out which players are outstanding left-fielders. Well, who qualifies as an outstanding left-fielder? Are they the players who can pitch with the most accuracy? If so, what is the accuracy cutoff?

If accuracy is not the metric, what about running speed? How fast a player may be able to run to catch a ball may be important. What about the ratio of caught balls to missed balls? How exactly do we decide who to include in the set of outstanding left-fielders?

The problem with a “set” such as “outstanding left-fielders” is that the term outstanding is vague. Notice that we enclosed the word set with quotation marks in the previous sentence. That’s because part of the definition of a set is to be well-defined. Since it is not exactly clear how to determine who an outstanding left-fielder is, we have no well-defined criterion. As such, the above description does not define a set.

Let’s do something different. This time, let’s niche down into something like this:

The set of all Major League Baseball players who hit at least 300 home runs in the 1990s.

Here, all we have to do is check the records of the players from the 1990s, which we can do here, and see who hit at least 300 home runs. Here are those players:

{ Mark McGwire, Ken Griffey Jr., Barry Bonds, Albert Belle, Juan Gonzalez, Sammy Sosa, Rafael Palmeiro, Jose Canseco, Frank Thomas, Fred McGriff, Matt Williams }

Notice the difference, one description was vague and open to interpretation, and as such, not everyone may agree on what players would be included. The other description was specific, and could be verified against the available records. The second description was not open to interpretation at all: we offered a very specific metric, and only those players meeting that requirement are included.

Typically, we use use capital letters such as A, B, C, …, X, Y, and Z to represent sets. That isn’t always the case, but is fairly common. In contrast, we typically use lowercase letters such as a, b, c, …, x, y, and z to denote elements.

Something else worth noting is that we enclose the elements of a set within curly braces {}, as demonstrated in Example 3.1.1.

Example 3.1.2

Let’s revisit the set defined in Example 3.1.1. Remember, only one of those descriptions actually defined a set, that being the set of “Major League Baseball players who hit at least 300 home runs in the 1990s”.

First, instead of repeatedly saying “the set of Major League Baseball players who hit at least 300 home runs in the 1990s”, we’ll use the capital letter M to refer to that set:

M = the set of Major League Baseball players who hit at least 300 home runs in the 1990s.

We can use lowercase letters to refer to specific players like so:

a	=	Joe DiMaggio
b	=	Ken Griffey Jr.
c	=	Babe Ruth
d	=	Mark McGwire
e	=	Mike Piazza
f	=	Barry Bonds
g	=	Rocky Marciano

We can go through and determine set membership for each of these players.

a ∉ M because Joe DiMaggio played baseball from 1936 to 1951, and as such didn’t play baseball in the 1990s, meaning he did not hit at least 300 home runs in the 1990s.

b ∈ M because Ken Griffey Jr. did hit at least 300 home runs in the 1990s. Even though he did play baseball for a brief time in 1989, as well as for a long time in the 2000s, that is irrelevant because we can still record how many home runs he hit in the 1990s all together, which was 382.

c ∉ M because Babe Ruth did not play baseball in the 1990s, and as such did not hit at least 300 home runs in the 1990s.

d ∈ M because Mark McGwire meets the requirement to be in M.

e ∉ M because even though Mike Piazza did play Major League Baseball in the 1990s, he did not hit enough home runs to be in M (he hit 240, 60 less than the required 300.)

f ∈ M because Barry Bonds hit at least 300 home runs in the MLB in the 1990s. As such, he meets the requirement for membership in M.

g ∉ M because Rocky Marciano did not hit at least 300 home runs in the MLB in the 1990s. As a matter of fact, Rocky did not play baseball professionally at all. Instead he was the Heavyweight World Champion Boxer, and was active from 1947 to 1951. So not only is this the wrong sport, but the time frame is also incorrect.

Building a Set

There are two primary ways to describe what kinds of elements are within some set.

One way to describe what elements are in a set is to simply list them all. Of course, this method is only practical if the desired set contains a small number of elements, though this method is perhaps the most specific, and leaves absolutely nothing to the imagination.

Example 3.1.3

Let A denote the set

A = {1, 3, 5, 7, 9, 11, 13, 15, 17}.

Let B denote the set

B = {-12, -9, -6, -3}.

Since order and repetition don’t matter when building a set, we also have that

B	=	{-12, -9, -6, -3}
	=	{-3, -6, -9, -12}
	=	{-6, -12, -3, -9}
	=	{-12, -9, -6, -12, -3, -3}
	=	{-12, -3, -9, -12, -6, -12, -3, -12}

Since we explicitly state which elements are in each set, it is extremely easy to determine if an element is in either set simply by inspection.

3.14 ∉ A because it is not one of the listed numbers in A.

11 ∈ A because it is explicitly listed within the set’s definition.

-6 ∈ B because it is explicitly listed in B’s definition.

13 ∉ B because it is not one of the listed numbers in B.

This method of building, or defining, a set is commonly called either the Roster Method, or the Exhaustive Method.

However, there is nothing stopping from us from defining sets that have infinitely many elements. When dealing with such a set, then the Roster Method or Exhaustive Method are somewhat inadequate. We could list enough elements to make the pattern obvious, and finish by using ellipses.

Example 3.1.4

Here, let A denote the set

A = {2, 4, 6, 8, 10, 12, …}

When defining set A, all the numbers we listed are positive even integers, hence we can reasonably assume that A refers to the set of all positive even integers. Of course, since there are infinitely many positive even integers, we have to use ellipses.

Let B denote the set

B = {1, 2, 4, 8, 16, 32, 64, …}

For B, it looks like all the numbers we listed are the non-negative integer powers of 2:

B = {2⁰, 2¹, 2², 2³, 2⁴, 2⁵, 2⁶, …}

Hence, we can reasonably assume that B refers to the set of all the powers of 2 where the exponent is a non-negative integer.

When using the Roster Method to list the first few elements of a set, it should be pretty clear what the pattern is. Anything that requires an elaborate setup to describe should be explicitly mentioned and described so as to prevent confusion. Remember, it should be obvious what elements are in the set.

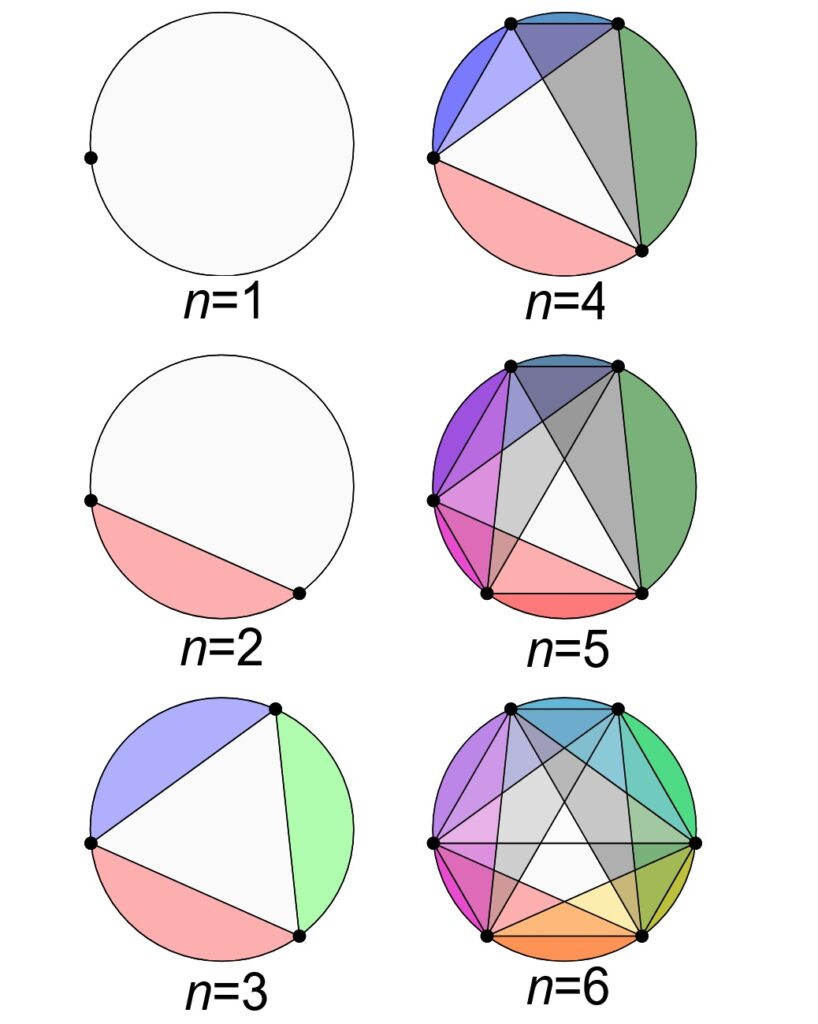
Figure 3.1.1: We can divide a circle into regions by placing points around it’s circumference, and connecting those points with those straight lines. Here, one way to arrange the points so as to maximize the number of regions is display where the n under each circle represents the number of points used. This particular image was slightly adapted from the image submitted by user Cmglee on the Wikipedia article here.

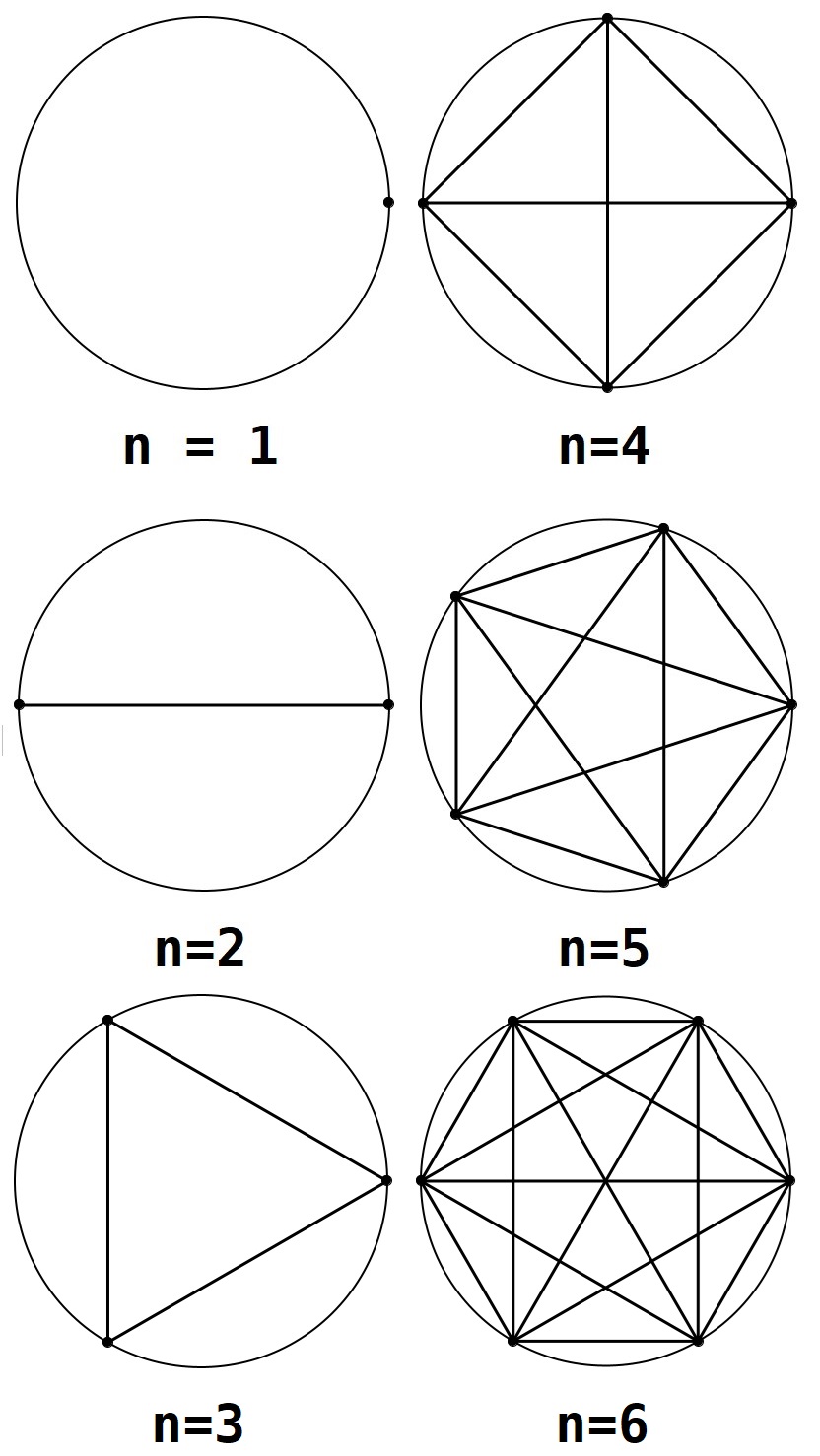
Figure 3.1.2: When points are placed equally distant away from each other, we don’t necessarily maximize the number of regions we can form by cutting the circle with straight lines. As such, we get a different set of numbers. These graphs were produced using Maple’s plotting tools.

Example 3.1.5

Consider the following set:

☒ = {1, 2, 4, 8, 16, …}

(Here, we use the symbol ☒ to refer to this set instead of a capital letter. The reason will be explained shortly.)

This almost looks like set B from Example 3.1.4, which was defined using powers of 2, hence we may think that ☒ is the set of all powers of 2 where the exponent is a non-negative integer.

Let’s reveal the next number in this particular set:

☒ = {1, 2, 4, 8, 16, 31, …}.

Hold on a second, 31 is not an integral power of 2! Hence, ☒ is not the set of all non-negative integer powers of 2.

So, what is it exactly? Is this set supposed be defined by some combination of arithmetic operators? If so, what are those operators? In what order are they applied?

As it turns out, this set describes the maximum number of regions a circle can be divided into by placing points around it’s circumference, and connecting those points with lines! Here are the next few numbers in the set:

☒ = {1, 2, 4, 8, 16, 31, 57, 99, 163, 256, …}.

There is a formula to calculate each number in the set:

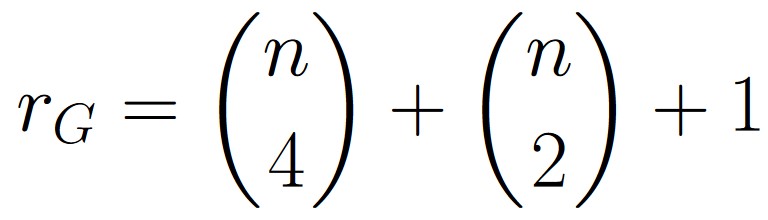
However, this formula involves something called “binomial coefficients” or “combinations” which are what those numbers enclosed in parenthesis are. We’ll discuss those later in this book, but for now, it may appear to be complete gibberish.

The point is that, even though the first few terms of a listed set may seem to follow one pattern, there may be multiple patterns that fit, and so listing only a few numbers at the start may not adequately describe the desired set.

That’s why we used the ☒ symbol to denote this set: we wanted to make clear that this is a very misleading set of numbers at first, and as such is ambiguous. Since it’s ambiguous, we should not have described the set this way, hence using a box with an x in it to denote the set.

For anyone wanting to learn more about this set of numbers, this Wikipedia article is a great starting point.

There is another set of numbers that begins this way:

{1, 2, 4, 8, 16, 30, 57, 88, 163, 230, …}.

This set is also related to circles, but this set of numbers occurs when placing points equally around a circle’s circumference. The difference is that this set does not necessarily represent the maximum number of regions a circle can be divided into, such as the set of numbers above.

Never be ambiguous when describing a set!

It is because of this ambiguity that can arise that another method of defining sets is more commonly used, called the Set Builder Method. This method requires the specification of some rule, or a list of conditions that determine whether an element is a part of the set. Typically, this method looks something like this:

A = { x | condition }.

There are a couple of different parts to this method, which we’ll color code below:

A = { x | condition }.

Lets go through each part:

A	This is simply the letter, or general symbol we use to refer to the set.
{}	These are the curly braces that are used to enclose the definition of the set. Every set is enclosed by curly braces.
x	This letter, or again some general symbol, is what we use to refer to some element within the set.
\|	This bar is used to separate the listing of the element from the condition. Usually, when reading out the definition of a set, the vertical bar can be translated to “such that”.
condition	The condition specifies what is true about the element x that makes it an element of the set A. In other words, the condition is what we use to test to see if some object is contained within set A.

As such, when we see something like

A = { x | condition }

we can read this definition as “A refers to the set of all elements x such that the condition is satisfied.” There is some flexibility to be had in this method, but examples of how this method can be used are demonstrated below.

Example 3.1.6

Here is a typical example of the Set-Builder Method of defining a set:

A = { n | n is an even integer }.

Based off of this definition we see that

6 ∈ A	-12 ∈ A
100238 ∈ A	-12300450678 ∈ A

Of course, there are infinitely many other numbers in A. On the other hand,

1 ∉ A	-13 ∉ A	100343 ∉ A
3.1415 ∉ A	-2.718 ∉ A

among infinitely many other numbers.

Sometimes, multiple conditions can be placed on a set using the conjunction operator discussed in Chapter 1 like so:

B = { x | x is an integer ∧ x > 10 }.

So, any number that is simultaneously an integer, and larger than 10 is included in B. Thus we have that

90 ∈ B

92 ∈ B

100100 ∈ B

and so on. On the other hand, we have that

-2 ∉ B

10 ∉ B

0.4335 ∉ B

because -2 is not larger than 10, because 10 is not larger than itself, and because 0.4335 is not an integer nor is it larger than 10, so it fails both conditions.

It is possible to specify one condition before the vertical bar | in the set’s description like so:

C = { x is an integer | x ≤ -4 }.

Here, we are implying that, before we even consider what the normal condition is, we are presupposing that only integers can be included in C. In other words, this definition is equivalent to saying that

C = { x | x is an integer ∧ x ≤ -4 }.

Of course, we could use the disjunction operator as well, like so:

D = { x | x is a multiple of 0.4 ∨ x is a negative integer }

As such, we find that

2.4 ∈ D

-12 ∈ D

-100.4 ∈ D

because 2.4 is a multiple of 0.4 (or it’s a negative integer), because -12 is a negative integer and a (negative) multiple of 0.4, and because -100.4 is a multiple of 0.4 (or it’s a negative integer). However,

1 ∉ D

because 1 is neither a multiple of 0.4 or a negative integer.

The Set-Builder Method is extremely useful to describe sets with infinitely many elements, however that does not mean it is not useful in defining sets with a finite amount of elements. This is especially true if there is a large number of elements in the set.

Example 3.1.7

Consider the following set:

X = { n is an integer | n² < 100 }

First, we know that we only have integers in X, because that is a condition for set inclusion.

The second condition is that the square of an integer must be less than 100. We can check a few numbers to be sure:

0²	=	0	<	100
1²	=	1	<	100
2²	=	4	<	100
3²	=	9	<	100
4²	=	16	<	100
5²	=	25	<	100

As a matter of fact we know that the first integer n where n² ≥ 100 is 10 since 10² = 100. As such, all the positive integers less than 10 are included in the set, so we have that

1 ∈ X	2 ∈ X	3 ∈ X
4 ∈ X	5 ∈ X	6 ∈ X
7 ∈ X	8 ∈ X	9 ∈ X

We also tested and verified that 0 ∈ X.

Since negative integers have positive squares, we also know that

-1 ∈ X	-2 ∈ X	-3 ∈ X
-4 ∈ X	-5 ∈ X	-6 ∈ X
-7 ∈ X	-8 ∈ X	-9 ∈ X

Any integer larger than 9, or less than -9 will not be included, because the smallest integer larger than 9 is 10, and 10² is not less than 100. Similarly, the largest integer smaller than -9 is -10, and (-10)² is also not less than 100.

As such, we know that all of the elements that are in X are the following:

X = {0, 1, -1, 2, -2, 3, -3, 4, -4, 5, -5, 6, -6, 7, -7, 8, -8, 9, -9}.

Even though we could list them, the Set-Builder Method at least gives us a rule to decide if some number is contained within the set. If we had simply listed the numbers, we wouldn’t know if there were some underlying condition, or if the numbers were simply chosen arbitrarily.

Of course, with a set like

Y = { n is an integer | n² ≤ 1000000000000 }

it would take a long time to fully list out the elements, unless we did something like this:

Y = {0, 1, -1, 2, -2, 3, -3, …, 999999, -999999, 1000000, -1000000}.

But we still prefer to work with the Set-Builder Method of describing Y because the Set-Builder Method is typically more succinct.

Example 3.1.8

Consider the following set:

Ψ = { n³ | n is an integer ∧ n² < 100 }.

Here, we use the capital Greek letter psi Ψ just to add some variety to the types of names we’ve been using for our sets.

It looks like Ψ consists of perfect cubes, but one of the conditions is that the square of the underlying integer must be less than 100. Let’s examine a short list of some of the integers. In the following table, we’ll color all of the cells in the n² column that satisfy the requirement in green, and we’ll color red all those that do not.

n	n²	n³
-10	100	-1000
-9	81	-729
-8	64	-512
-7	49	-343
-6	36	-216
-5	25	-125
-4	16	-64
-3	9	-27
-2	4	-8
-1	1	-1
0	0	0
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	729
10	100	1000

Any integer less than -10 will have a square greater than 100, as will any integer greater than 10, so we don’t need to examine any more integers.

Remember that Ψ does not consist of those perfect squares, but instead consists of the corresponding cubes, which are listed in the right-most column of the above table, hence we know that

Ψ = { 0, 1, -1, 8, -8, 27, -27, 64, -64, 125, -125, 216, -216, 343, -343, 512, -512, 729, -729 }.

Size of a Set

From the examples listed on this page, we’ve seen sets that can have vastly different numbers of elements. Some sets have a finite number of elements, meaning that if we started to list out all of that set’s elements, we would eventually be able to stop and have all elements written down. In contrast some of the sets we’ve seen have had infinitely many elements, meaning if we start listing elements and stop at any point in time, there would be elements missing.

For finite sets, knowing the number of elements contained within can be useful.

Cardinality

For any finite set A, we use the notation

|A|

to refer to the number of elements in A. We refer to the number of elements in A as the cardinality of A.

Even though we do not speak of a cardinality of an infinite set (yet), it is technically correct to say that the cardinality of C is countably infinite. This idea will be explored later when we talk about the different special sets of numbers.

Example 3.1.9

Consider the following sets:

A	=	{ x³ \| x is an integer and \|x³\| < 100 }
	=	{ 1, -1, 8, -8, 27, -27, 64, -64 }

B	=	{ x² \| x is an integer and x² < 100 }
	=	{ 1, 4, 9, 16, 25, 36, 49, 64, 81 }

C	=	{ 2n \| n is an integer }
		{ 0, 2, -2, 4, -4, 6, -6, 8, -8, 10, -10, … }

We see that both A and B are finite sets, so we can see that they have the following cardinalities:

|A| = 8

|B| = 9

We see that C is an infinite set, so we do not speak of it’s cardinality.

Care must be taken when we are dealing with sets that contain a wide variety of items. If a set has an element that is itself a set with multiple items, the multiple elements of that inner set do not count towards the outer set’s cardinality.

Example 3.1.10

Consider the set

X = { a, b, c, 1, 2, 3, x, y, z, {1, 2, 3}, {{1}, 2, 3}, {a} }.

This is a set with a wide variety of different types of objects. There are numbers, letters from the English alphabet (the a, b, c, x, y, and, z are not referring to variables in this particular case, just the letters themselves.), and even a few sets!

Let’s list out all of the elements contained within X in a table:

a	1	x	{1, 2, 3}
b	2	y	{{1}, 2, 3}
c	3	z	{a}

Notice that the element a is not the same thing as the element {a}: one is simply a letter, and the other is a set (containing the letter), and so are different elements entirely.

The same is true for the elements 1, 2, 3, {1, 2, 3}, and {{1}, 2, 3}. The element {1, 2, 3} is a set (though it contains many elements itself, the set only counts as one element for X.)

As such, there are no repeated elements in X, and since all are different, they all count towards the cardinality of X, meaning that we have

|X| = 12.

Of course the set {1, 2, 3} has its own cardinality:

| { 1, 2, 3 } | = 3.

But it is still 1 set, and it only counts for 1 element when considering the cardinality of X.

Similarly, we have that

| { {1}, 2, 3 } | = 3.

Contrast the above set with the following:

| { {1}, {2, 3} } | = 2

because the 2 and 3 are included in a single set within { {1}, {2, 3} }.

The Book ofFoundational Mathematics

Quick Links

Sets

Intuitively Defining a Set

Set, Element, Member

Example 3.1.1

Example 3.1.2

Building a Set

Example 3.1.3

Example 3.1.4

Example 3.1.5

Example 3.1.6

Example 3.1.7

Example 3.1.8

Size of a Set

Cardinality

Example 3.1.9

Example 3.1.10

The Book of
Foundational Mathematics