How Do You Calculate Rook Polynomials?

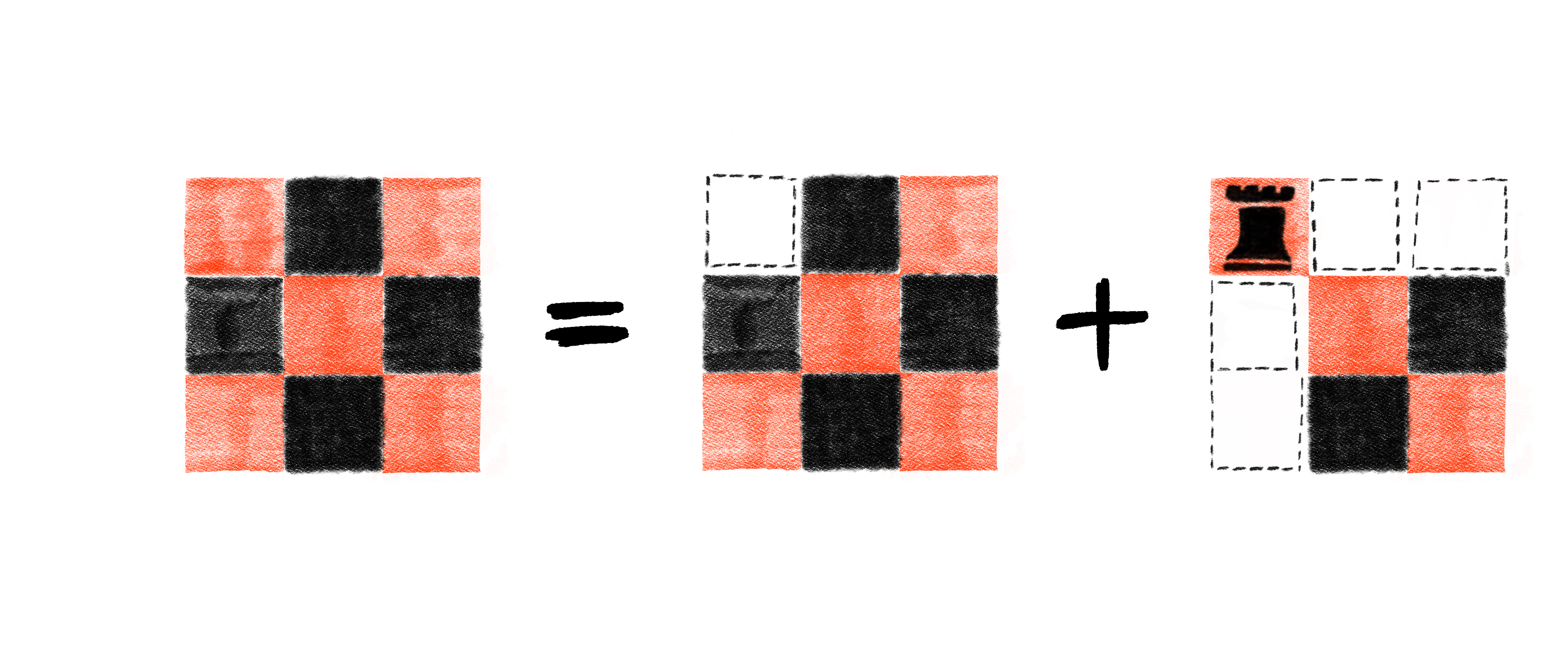
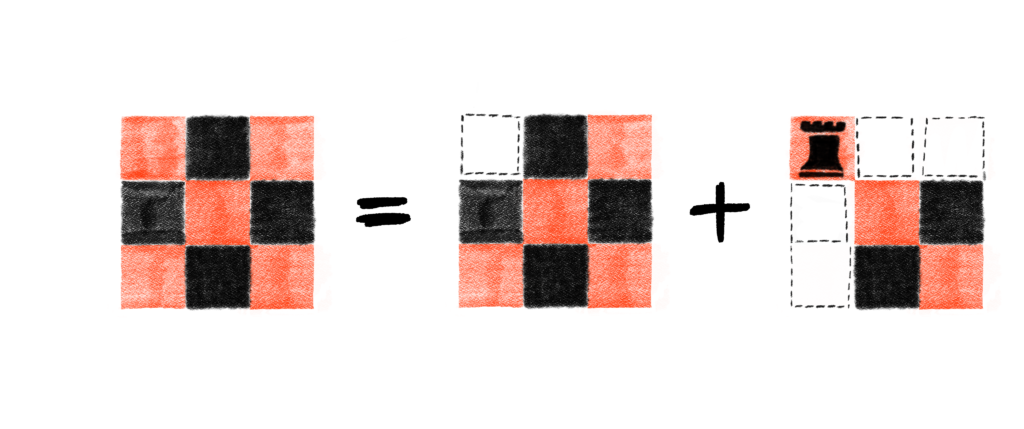
Ideally, we’d like to avoid having to exhaustively count the number of ways to place rooks on the board in such a way that they don’t attack each other. After all, the whole point is to use Rook Polynomials to do the counting for us. Doing the counting first, then constructing the Rook Polynomial defeats the purpose entirely. Before we figure out a smart way of doing this, we should get a handle on how to describe the chessboards for which we want to construct polynomials.

Describing Chessboards

As seen in the previous post, the “chessboards” we could consider don’t necessarily need to be square. They could have any number of rows and columns, so initially, we could try describing a chess board as an ordered pair like so:

This works perfectly well for simple chessboards like the following 2-by-2 and 3-by-3 boards:

We could refer to these boards as C₁ = (2, 2) and C₂ = (3, 3) respectively. The problem is that this does not give us a way to describe any boards that have restricted cells. Take this board for example:

Even though this board has two rows and two columns, it is missing a square in the upper-left corner. How do we describe this board? One thing we could do is provide a set of ordered pairs describing which cells are restricted, along with the number of rows and columns it has. First, note that we could represent this exact same board in the following way:

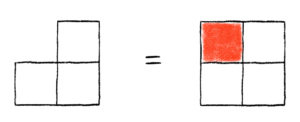
We still have two rows and two columns, but now we have all four squares. We just use the color red to signify that we can’t place a rook in that square. As previously mentioned, we can supply a set of ordered pairs representing which cells are restricted. In this case we could say R₃ = {(1, 1)}. Now we could describe this chessboard using a 3-tuple: C₃ = (2, 2, R₃).

This description seems rigorous enough for our purposes, so in general, we’ll use this scheme to describe what ever chessboard we want:

We can see this notation in action with a few examples.

Example: A 3-by-3 Board Without Any Corners

We can do the same thing we did before, where we consider a full 3-by-3 board with red squares representing any “missing” or “restricted” cells.

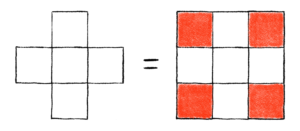
Here, the restricted cells are at positions (1, 1), (1, 3), (3, 1), and (3, 3). So our set of restricted cells will be

Now we can describe our board using the ordered 3-tuple

We could also just write the set inside the 3-tuple, which would look like this:

Example: A 3-by-3 Board With Some Other Missing Squares

Again, we consider the full 3-by-3 board with the missing squares colored red.

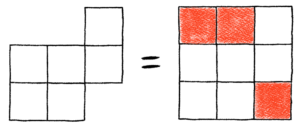
In this case our set R will be

We describe this board using the 3-tuple

Example: A Rectangular Board With a Missing Corner

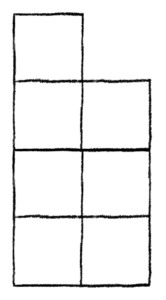
In our last example, we will draw the full 4-by-2 board with the missing square colored red.

Here, we only have one restricted cell, so we have that

We describe this last board using the 3-tuple

Decomposing Chessboards: C^* and C⁺

Now that we have a scheme for describing chessboards, we can use it to describe two special kinds of chessboards.

In the previous post, we found the Rook Polynomial for a full 3-by-3 board by considering two different cases. In the first case, we said there was a rook at cell (1, 1). In the second case, we said there was no rook at cell (1, 1). These two cases had different consequences, and since these two cases are mutually disjoint, adding whatever resulted together yielded the final result.

The header image for this post serves as a nice reminder of what happens when we consider these two cases.

Case One: A Rook Is Placed at Cell (1, 1)

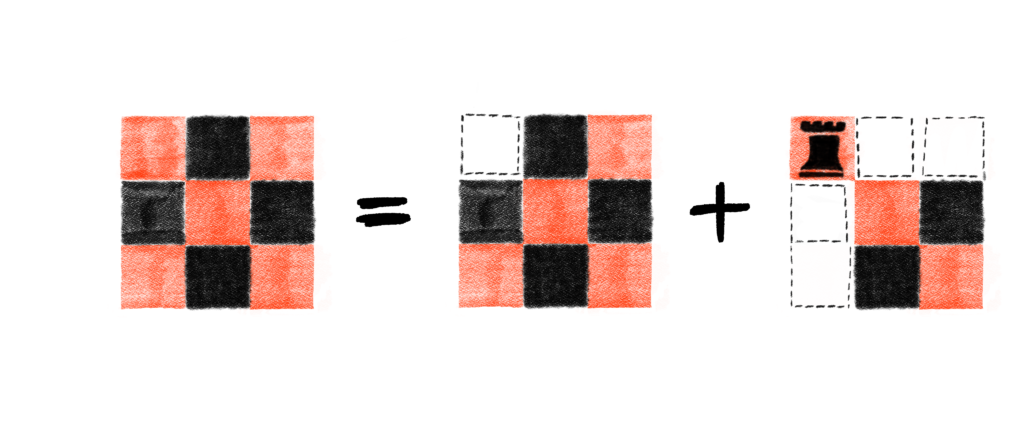
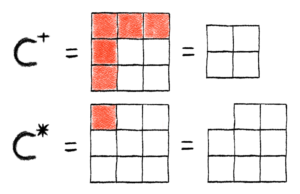
Here, because a rook is placed at cell (1, 1), no other rook can be placed on row 1, and no other rook can be placed on column 1. This effectively leaves a 2-by-2 board left without any restricted cells. Because we obtained this new board by placing a rook at a specific cell, we’re going to denote this new board as C⁺. Using our new notation, we first note what the set R is, which in this case is going to be

So this new board would be denoted

But as we just noted, this essentially just leaves the full 2-by-2 board left on which to place rooks, so as it turns out, we could write

Case Two: No Rook Is Placed at Cell (1, 1)

Here, since we know that no rook is placed at cell (1, 1), there are only 8 cells left for rooks to be placed (we just said that no rook is at cell (1, 1), so we need to restrict that cell from all rooks.) In this case we have that

The new chessboard, which is obtained by restricting rooks from being placed on a specific cell is denoted C^*. In this case we have that

Something worth pointing out now is that C⁺ and C^* are both formed with reference to the exact same cell on the exact same board. For instance, you can’t form C⁺ by forcing a rook onto cell (1, 2), and then form C^* by restricting rooks from cell (3, 2). The point in forming C⁺ and C^* is to do case work by considering what happens when a rook is either placed or restricted from some specific cell.

Finishing up, note that in this example, C⁺ and C^* refer to the boards in this following picture:

Simple Boards

With notation out of the way, we can start working on a general strategy for calculating Rook Polynomials. Let’s start by considering 3 kinds of simple boards that will be really easy to work with.

The 1-by-1 Board

This is the the most trivial board we can work with.

We can refer to this board as C_{1, 1}, which lets us write the Rook Polynomial as

Just as a brief reminder, this polynomial says that there is exactly 1 way to place 0 non-attacking rooks on this board, and that there is exactly 1 way to place 1 non-attacking rook on this board, and 0 ways to place 2 or more non-attacking rooks on this board. We could make this more explicit by writing the polynomial as

The 1-by-n Board

Here, we have a board with one row, and n columns, which would denote as C_1,n, and it would look something like this:

Of course, there is always exactly one way to place 0 non-attacking rooks on this board (and really, on any board), so that’s taken care of.

We can also easily reason about the number of ways to place 1 non-attacking rook on this board. Because the board is 1-by-n, there are n cells on which to place our lone rook, so there are n ways to place a non-attacking rook on this board.

Because there is only one row on this board, the first place rook prevents any other rook from being placed, so the maximum number of rooks that can be placed on this board is 1.

So the Rook Polynomial for this kind of board is going to be

For a quick and easy example, consider C_1,3.

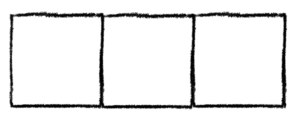
We have that R(C_1,3, x) = 1 + 3x.

The m-by-1 Board

This is the chessboard with m rows, and one column.

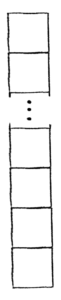
By the exact same reasoning used for 1-by-n boards, because there are m rows, and one column, we have that

For another quick example, consider C_4,1.

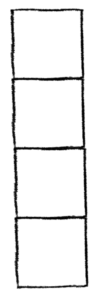
Here, we have that R(C_4,1, x) = 1 + 4x.

Knowing the Rook Polynomials for these simple boards is what is going to allow us to work out Rook Polynomials for more complex boards without doing any exhaustive counting beforehand.

The 2-by-2 Board

We start with a small example for which we already know what the Rook Polynomial is (which can be easily obtained by exhaustive counting/inspection.) The Rook Polynomial for this board (denoted C_2,2) is

Again, we start by doing some case work.

Case One: A Rook Is Placed at Cell (1, 1)

If we place a rook at (1, 1), then row 1 and column 1 are restricted from any other rook. This leaves only 1 square left: the 1-by-1 board C_1,1. Remembering we have a special notation for this kind of chessboard where a rook is placed at a specific cell, this gives us that, in this case,

We already know the Rook Polynomial for C_1,1, so we have

However, keep in mind, that in this configuration, there is already a rook on the board (at cell (1, 1).) R(C_1,1, x) only tells us the Rook Polynomial for C_1,1 without reference to the “surrounding” board. To account for the fact that there is already a rook on the board in this case, we essentially need to increment each exponent in the polynomial. This can be achieved by simply multiplying the polynomial by x:

Case Two: No Rook Is Placed at Cell (1, 1)

Here, since no rook is placed at (1, 1), we essentially restrict this cell from any rook. Going back to the special notation we had for restricting a cell on a board (C^*), we have that C^* = (3, 3, { (1, 1) }). This board is easy enough to handle by inspection, so we’ll just note that

For reference, this is the board obtained by restricting cell (1, 1):

The Final Answer

We did this by considering two cases. In one case, we placed a rook at (1, 1). In the other case, we restricted (1, 1) from any rooks. These two cases are disjoint, and cover every possibility. By the rule of sum, we should then be able to add up whatever results we got to get our answer. Seeing as how we have two Rook Polynomials, both of which encode the number of ways to place rooks on their respective boards, we should simply be able to add the polynomials together:

Great! Our new method agrees with our previous method.

The 3-by-3 Board

By virtue of the fact that there are simply many more cells, this will take a bit more work. We already know that for C_3,3 we have that R(C_3,3, x) = 1 + 9x + 18x² + 6x³, again from the previous post.

We can probably make things easier for ourselves by being a bit clever about where we choose to place or restrict our rook. So far, we’ve been using or restricting cell (1, 1), but what about the center cell (2, 2)? Let’s see what happens. Again, we have two cases to consider.

Case One: A Rook Is Placed at (2,2)

If a rook is placed at (2, 2), that means we’ve placed one rook so far (so we’ll need to increment exponents in the resulting Rook Polynomial, which is accomplished by multiplying it by x.) Here’s what happens:

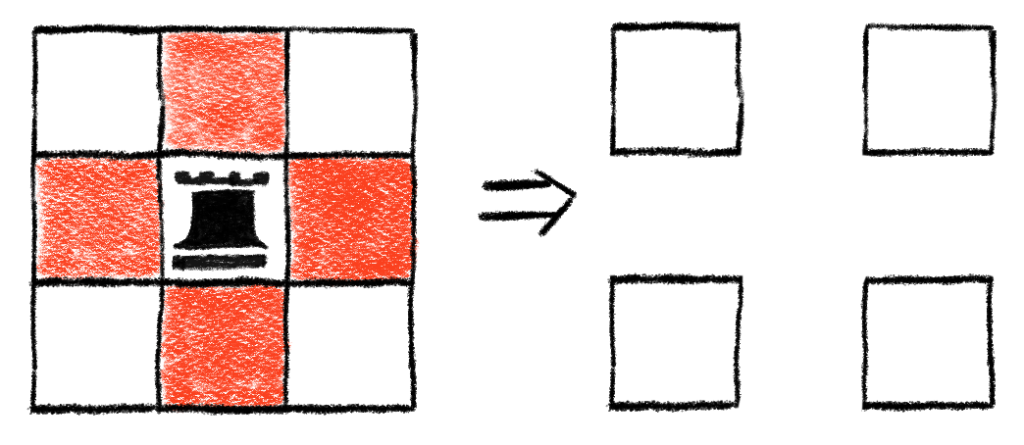
So, it looks like only the four corner cells are vacant for any additional rooks. We notice that there are gaps surrounding each cell, but does it matter? Once a we place a rook, that new rook’s row and column are totally restricted from other rooks. It’s not like the squares in the middle row and column just disappeared, leaving voids that can’t be crossed. They’re still there, just restricted. A rook can still capture across those gaps. Essentially, we can treat those gaps like they are not there, so we can “push” the rows and columns together to form an “equivalent” board. This yields the following picture:

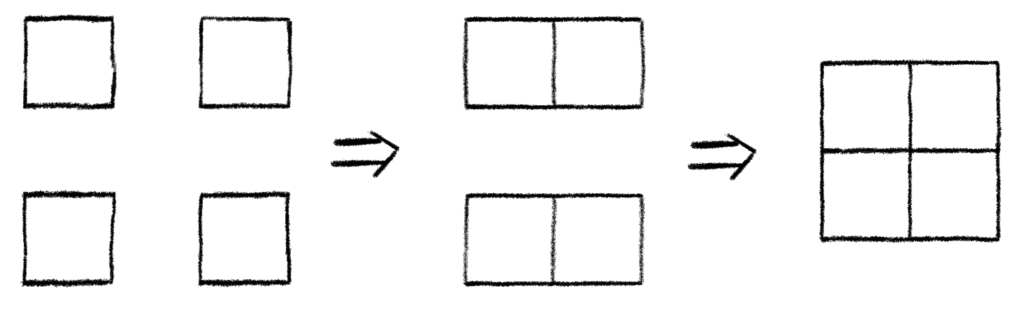
This is just C_2,2, which we already know how to deal with. Again, keeping in mind there is already one rook on the board, we’ll need to increment the exponents in the Rook Polynomial for C_2,2 in order to get the correct counts.

Case Two: No Rook Is Placed at (2, 2)

Now we are left with this situation:

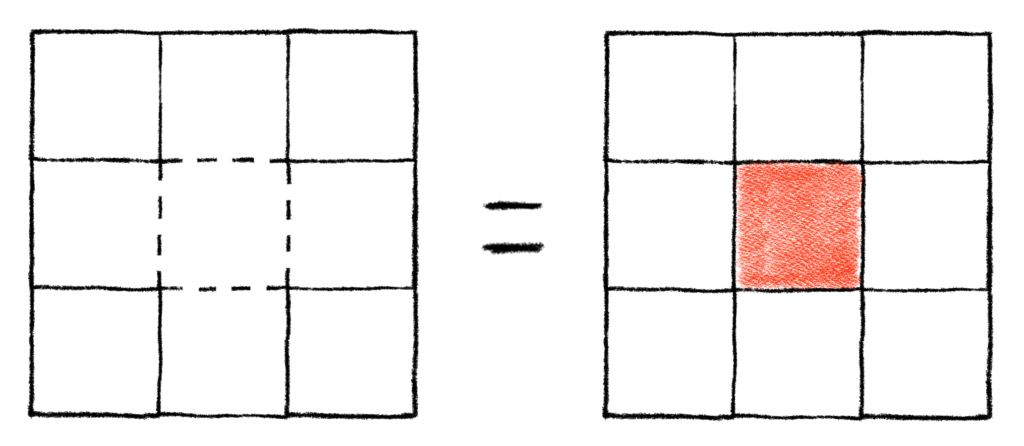
Perhaps our “clever” rook placement didn’t simplify things too much for us. Now we have 8 squares, with the center square missing. We could try and figure out R(C^*, x) by inspection, but we could also try decomposing C^* into its own sub-boards, which we could call C₁⁺ and C₁^* respectively. This will let us build up the Rook Polynomial recursively. We’ll just need to pick another unrestricted cell we can use for case work. We already know that (2, 2) is off limits for another rook. We should probably use one of the cells in the center row or column, which would let us keep the restricted cells together, though it won’t matter too much which cell we ultimately pick for our decomposition. Let’s just use (1, 2).

Using our strategy, we would have that

This gives us the following picture:

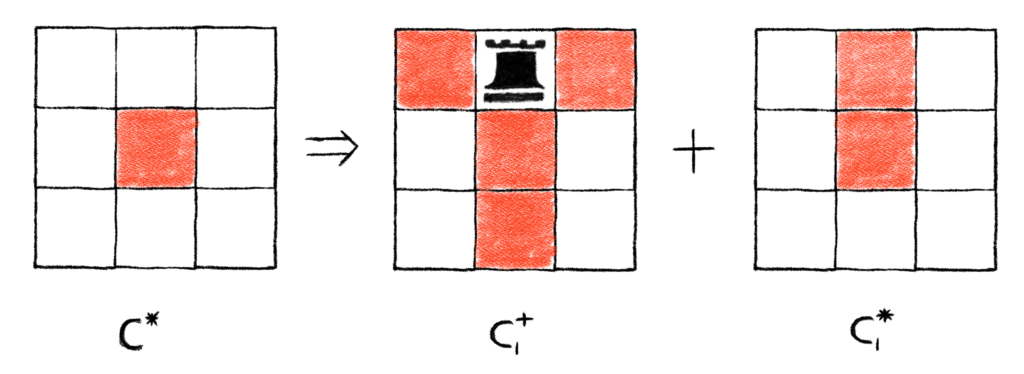
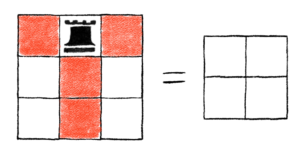
One thing to notice really quickly is that C₁⁺ = C_2,2, so we have that R(C₁⁺, x) = R(C_2,2, x) = 1 + 4x + 2x².

But C₁^* still looks like a pain to do by inspection. We can try and do yet another decomposition. This will at least get us something simpler, and hopefully something simple enough to by inspection, because that would be our third recursive step and this is getting a bit out of hand. We’ll do one more decomposition, this time we’ll us cell (3, 2), and we’ll call each respective board C₂⁺ and C₂^*. This would give us that

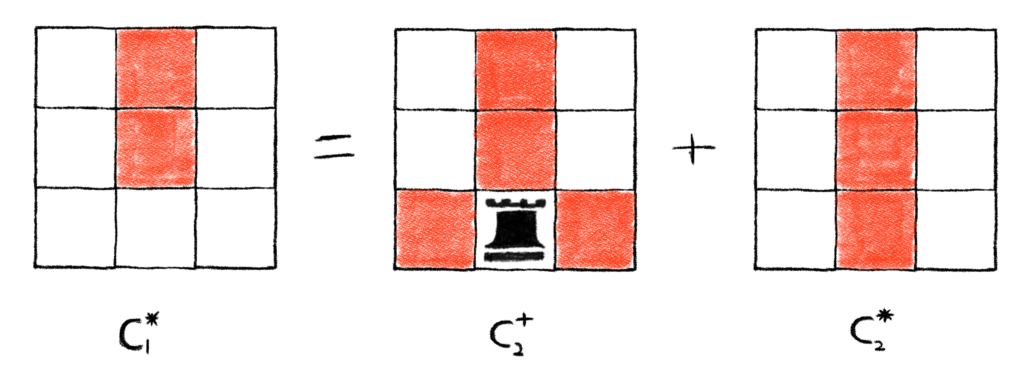
Again, before moving on, note that C₂⁺ = C_2,2 by the same reasoning as before. Thus,
R(C₁⁺, x) = R(C_2,2, x) = 1 + 4x + 2x². Again noting that we could ignore red squares and look at simplified boards gives us the following picture:

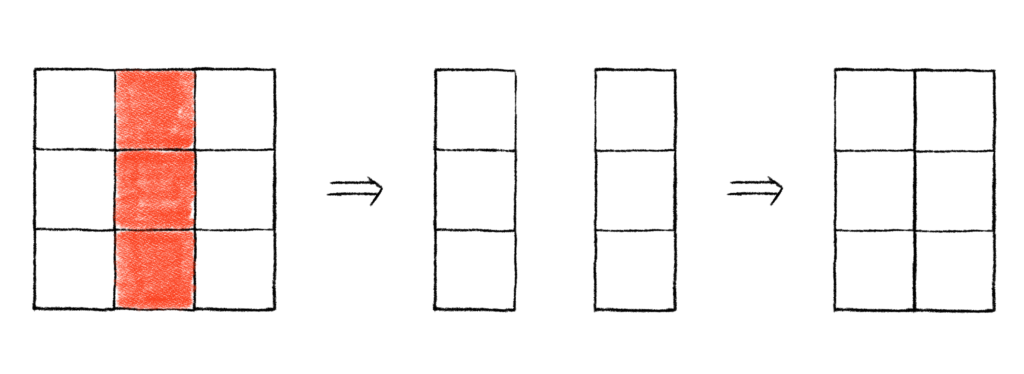
Ok, so the simplified version of C₂^* is easy enough to handle by inspection. We’ll get that
R(C₂^*, x) = 1 + 6x + 6x². We are now finally in a position to calculate our result.

The Final Answer

Let’s recap. We have the following set of equations:

We can calculate R(C₁^*, x) using what we just figured out:

Now we can substitute R(C₁^*, x) into equation (2):

Now we can substitute R(C^*, x) into equation (1):

Holy moly! That was quite a bit of work, but this answer agrees with what we found in the previous post. Honestly, typing out all of the steps took some time for me, but using this decomposition trick can speed things up now that we know the general procedure.

The 3-by-3 Board Without Corners

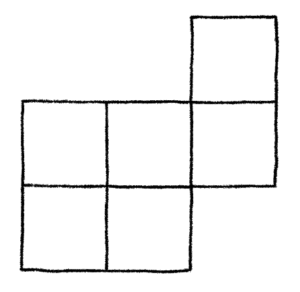
In order to speed things up, I won’t type out every step, but will just resort straight to using the decomposition. Here’s the board:

Here, I am going to decompose this board on the (2, 1) cell. This results in the following picture:

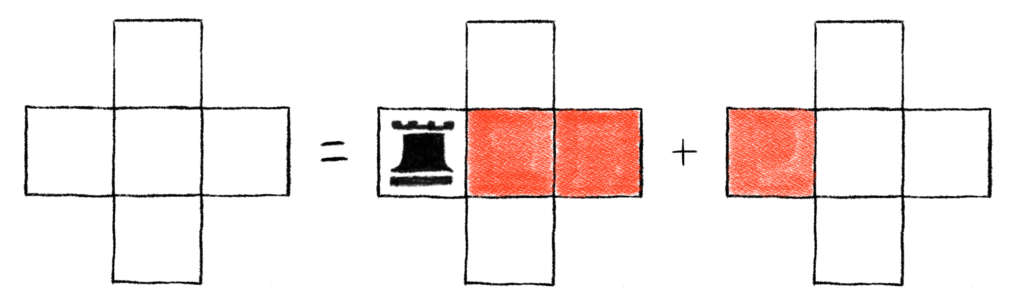
These boards are easy enough to do by inspection. I’d like to point out that C⁺ is C_2,1 which is one of the easy boards we examined much earlier in the article. Doing this by inspection yields the following:

The General Strategy

In summary, our general strategy is the following:

This formula works because it’s essentially encoding case work. xR(C⁺, x) encodes the case where we place a rook at cell (i, j) of the board, and R(C^*, x) encodes the case where we don’t place a rook at cell (i, j). This lets us construct Rook Polynomials through a recursive process, without having to do exhaustive, brute-force counting.

For relatively small boards, this process works quite well. As long as you don’t have to type out every step like I did, the process goes by relatively quickly. Small boards are easy enough to do by inspection as demonstrated earlier. That’s the goal of this recursive procedure: decompose a board until you have simple boards that are extremely easy to calculate by inspection, then substitute back in until you get the desired polynomial.

Larger Boards

After a certain point, this process does get unwieldy. It’s still faster than brute-force counting, but that doesn’t change the fact that it can be quite a pain to manage. The good news is that this recursive process does lend itself well to automation, so in the next post I’ll go through the process of getting a program to do this for us.